游戏开发中的数学和物理算法（17）：平移

点的平移，可以通过矩阵相加和相乘来模拟。

2D加法平移：

例如：
点A(20,30)，向右移50个像素，向下移100个像素，得到A'。

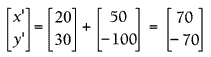
那么A'(70,-70)。

3D加法平移：

例如：

计算机中实现：

Matrix3X1 translate3DByAddition(Matrix3X1 start, Matrix3X1 trans)
{
      Matrix3X1 temp;
      temp = addMatrices(start,trans);
      return temp;
}

 

2D乘法平移：

例如：

计算机中的实现：

Matrix3X1 translate2DByMultiplication(Matrix3X1 start,float dx, float dy)
{
         Matrix3X3 temp;
         Matrix3X1 result;

         //Zero out the matrix.
         temp = createFixed3X3Matrix(0);

         //setup the 3x3 for multiplication;
         temp.index[0][0] = 1;
         temp.index[1][1] = 1;
         temp.index[2][2] = 1;

         //put in the translation amount
         temp.index[0][2] = dx;
         temp.index[1][2] = dy;

         result = multiplyMatrixNxM(temp,start);
         return result;
}

 

3D乘法平移：

例如：

计算机中的实现：

Matrix4X1 translate3DByMultiply(Matrix4X1 start,float dx, float dy,float dz)
{

         Matrix4X4 temp;
         Matrix4X1 result;

         //Zero out the matrix.
         temp = createFixed4X4Matrix(0);

         //setup the 4X4 for multiplication;
         temp.index[0][0] = 1;
         temp.index[1][1] = 1;
         temp.index[2][2] = 1;
         temp.index[3][3] = 1;

         //put in the translation amount
         temp.index[0][3] = dx;
         temp.index[1][3] = dy;
         temp.index[2][3] = dz;

         result = multiplyMatrixNxM(temp,start);
         return result;
}