AC自动机学习笔记
再不更新这里都长草了
前置知识
- KMP
- Trie树
前言
AC自动机是一个字符串匹配算法,与KMP的区别在于,AC自动机可以用\(O(\sum |s_i| + |S|)\)的复杂度在文本串中同时查找多个模式串,例如这道题
对于初学者 就是我 而言,可以简单地将AC自动机理解为KMP + Trie树,整个算法分为三步:
- 将所有的模式串建成一颗Trie树
- 求出Trie树上每一个节点的失配指针(fail)(类似KMP的next)
- 将文本串在Trie树上进行匹配
算法过程
建立Trie
这一步和普通的字典树一样,不解释
void insert(string& s) {
int p = 0;
for(int i = 0; i < s.length(); i++) {
if(t[p][s[i] - 'a'] == 0) {
t[p][s[i] - 'a'] = ++tot;
}
p = t[p][s[i] - 'a'];
}
num[p]++;
}
求失配指针
\(fail_u\)的定义为,Tire树内所有字符串的所有前缀中,后缀匹配长度最大的的位置;如下图中,\(fail_i = j\)
(图中不同颜色的边代表字符)
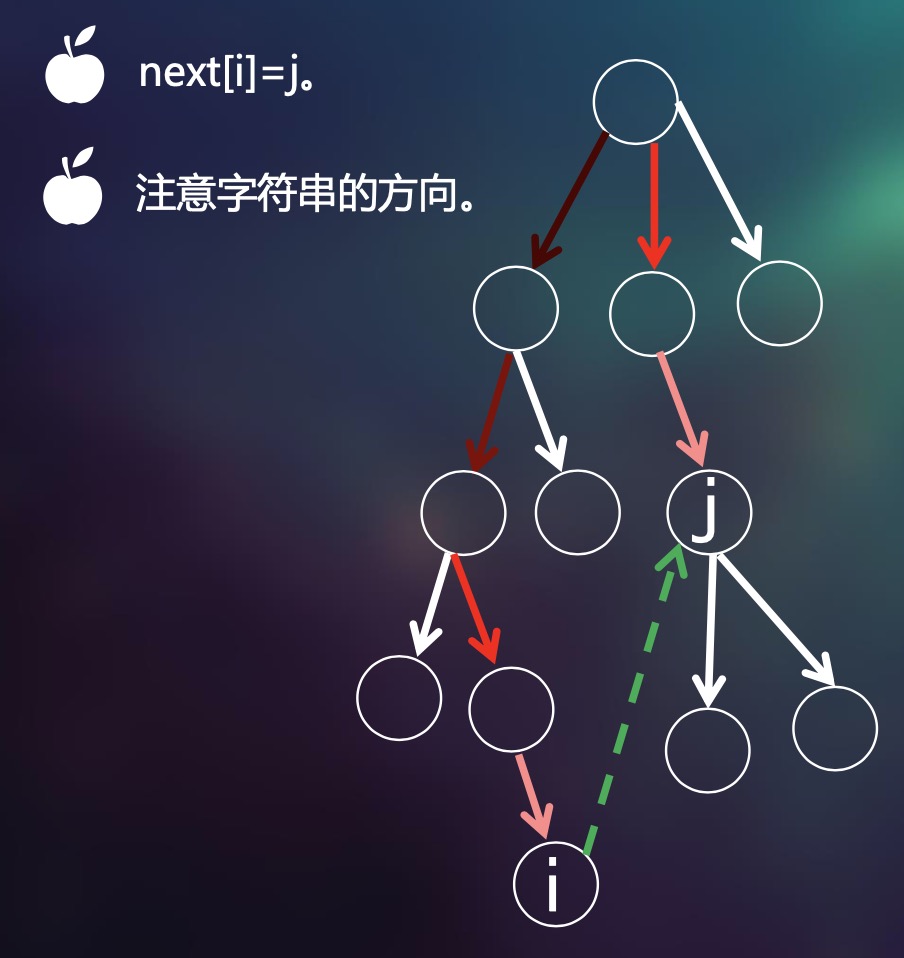
如图,节点\(i\)与节点\(j\)的后缀匹配最长,所以\(fail_i = j\)
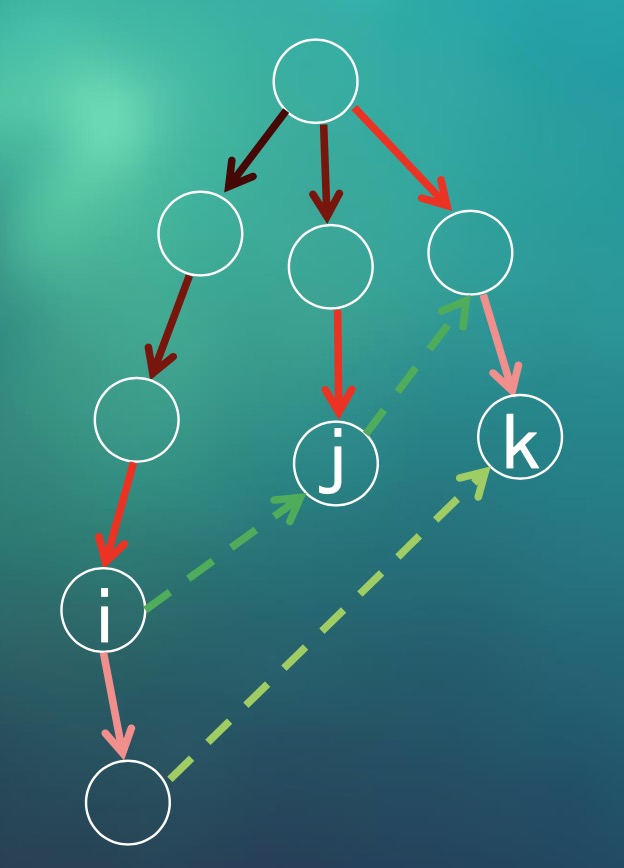
如图,\(fail_i = j\),则\(i\)的粉色子节点(此处用颜色表示字符)必然也与\(j\)的粉色子节点有最长的后缀,因此该子节点的\(fail\)指针就是\(k\)
具体求法:对于\(u\)的子节点\(v\),其\(fail\)指针为\(u\)的\(fail\)指针的字符与\(v\)相同的子节点,证明很简单,因为\(fail_u\)与\(u\)的后缀匹配最长,而\(v\)节点上的字符\(i\)显然与\(trie[fail_u][i]\)上的字符\(i\)相同,所以\(fail_v = trie[fail_u][i]\)
理解原理后我们很容易就能求出所有的\(fail\)指针:在字典树上跑一遍BFS,根节点的子节点的\(fail\)指针显然为0,所以先将这些点放入队列;
对于每一个当前搜索到的节点\(u\),它的\(fail\)指针肯定已经被求出,所以我们只需要枚举它的所有子节点t[u][i],建立\(fail\)指针 fail[t[u][i]] = t[fail[u]][i]
代码如下:
void getFail() { //bfs构建fail数组
queue<int> q;
for(int i = 0; i < 26; i++) { //根结点下面直接连的第一层结点,fail直接指向根结点0
if(t[0][i]) {
q.push(t[0][i]);
}
}
while(!q.empty()) { //队列中维护能够拓展fail值的结点
int u = q.front(); q.pop();
for(int i = 0; i < 26; i++) {
if(t[u][i]) {
//失配时,以trie[u][i]结尾的后缀尽量在trie中找一个与之相同的前缀(类似KMP)
fail[t[u][i]] = t[fail[u]][i];
q.push(t[u][i]);
} else {
//节点不存在,往上连,最多回到根结点0, 注意是trie不是fail数组
t[u][i] = t[fail[u]][i];
}
}
}
}
字符串匹配
这一部分理解难度不大,看代码注释即可:
int query(string s) {
int p = 0, res = 0; //p表示trie中的结点,res表示总和
for(int i = 0; i < s.length(); i++) {
p = t[p][s[i] - 'a']; //获取当前节点
for(int j = p; j != 0 && num[j] != -1; j = fail[j]) { //从p开始一直往上跳
res += num[j]; //num[j]表示以当前位置结尾字符串的总数,它们肯定都是
num[j] = -1; //避免重复计算
}
}
return res;
}
用\(p\)表示将字符串在\(Trie\)树上匹配时的位置,在每一轮循环中以\(p\)为起点向上跳,寻找匹配即可
复杂度分析
Trie树的大小为\(\sum |s_i|\),建立\(fail\)指针的复杂度与其相同,遍历文本串需要\(O(|S|)\),总时间复杂度为\(O(\sum |s_i| + |S|)\)



