COCI. RIJEKA

---

COCI.RIJEKA

题目类型：虚拟题目 时间限制：1.0s 空间限制：64.0MB 提交文件大小限制：100.0KB 提示：%I64d & %I64u

 

一条大河边上有M+1个村庄，村庄从0到M依次编号，，每个相邻村庄间的距离为1.MIRKO 住在0号村庄，他要驾船到M个村庄去，沿途有N个人要上船并到自己的目的地。MIRKO将送每一个人到他们的目的地，并最后将船停在M村庄。他的船足够大能装下所有的人，问他要航行的最短距离是多少？
一个例子。A要从村庄2到村庄8，B要从村庄6到村庄4。MIRKO可以先从0到2让A上船，然后到6，让B上船，然后到4让B下，然后到8，最后到M。
INPUT
第一行两个整数 N and M (N ≤ 300 000, 3 ≤ M ≤ 10^9).
接下来N行,每行两个整数,表示人们的要求.
OUTPUT
一个数,表示最短距离.
SCORING
In test cases worth a total of 40% points, N ≤ 5000 will hold.
In test cases worth a total of 50% points, M ≤ 2000000 will hold.
EXAMPLE TEST DATA
input
2 10
2 8
6 4
output
14
input
8 15
1 12
3 1
3 9
4 2
7 13
12 11
14 11
14 13
output
27

 

 

 

---

Problem：

题意还是比较清楚，求最小情况

 

---

Solution：

刚开始我们可以找找规律，看看特殊情况之类的

首先我们必然会走的路：

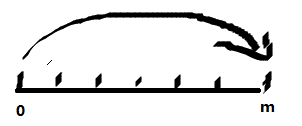
我们需要从0走到m

那么如果一个任务是是正向的

a->b a<=b的话，那么我们可以顺路得完成，不用多余的路

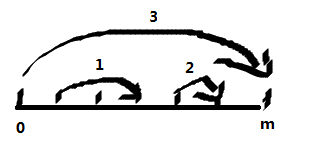
1和2都被顺路完成

而3是从0-m是最长的，我们就可以知道，如果任务是a->b a<=b的都可以被忽略，因为都可以被顺路完成

 

那么我们现在就只用考虑a->b a>b 倒着走的

逆向的情况根据刚刚我们正向分析的性质，也只到包含关系的内部可以省略

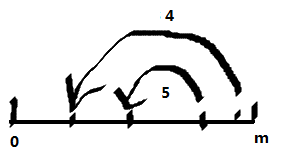
5可以省略

所以最后我们只用考虑的情况是

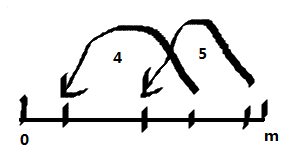
考虑我们是把4完成了，再完成5，还是4,5一起完成？

我们发现4,5一起完成会少走他们交集的那么段路

 

并且我们发现多个情况，也是一起完成是会更优

所以我们就有了贪心策略

只有有交集的都一起完成，否则就单独完成

 

---

附上代码：

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+12;
int n,m;
struct node
{
    int l,r;
    bool operator < (const node & other )const 
    {
        if(l==other.l) {return r<other.r;}
        return l< other.l;
    }
}edge[N];
int cnt;
long long f[N];

int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    scanf("%d%d",&n,&m);
    int a,b;
    for(int i=1;i<=n;i++) 
    {
        scanf("%d%d",&a,&b);
        if(a<=b) continue;
        edge[++cnt]=(node){b,a};
    }
    sort(edge+1,edge+cnt+1);
    int mx=0;int temp=cnt;cnt=0;
    for(int i=1;i<=temp;i++) 
    {
        if(edge[i].r<=mx) continue;
        edge[++cnt]=edge[i];
        mx=max(mx,edge[i].r);
    }
    
    f[1]=1LL*edge[1].l+(long long)(edge[1].r-edge[1].l)*3;

    int l=edge[1].l,r=edge[1].r;int id=1;
    for(int i=2;i<=cnt;i++) 
    {
        if(edge[i].l<=r) 
        {
            f[i]=f[id-1]+(long long)(edge[i].r-l)*3+1LL*(edge[id].l-edge[id-1].r);
            r=max(r,edge[i].r);
        }
        else 
        {
            f[i]=f[i-1]+(long long)(edge[i].r-edge[i].l)*3*1LL+1LL*(edge[i].l-edge[i-1].r);
            l=edge[i].l;r=edge[i].r;id=i;
        }
    }
    long long ans=f[cnt]+1LL*(m-edge[cnt].r);
    printf("%lld\n",ans);
    return 0;
}