BZOJ#4407. 于神之怒加强版

---

4407: 于神之怒加强版

Time Limit: 80 Sec  Memory Limit: 512 MB
Submit: 1302  Solved: 582

Description

给下N,M,K.求

Input

输入有多组数据，输入数据的第一行两个正整数T,K，代表有T组数据，K的意义如上所示，下面第二行到第T+1行，每行为两个正整数N,M，其意义如上式所示。

Output

如题

Sample Input

1 2
3 3

Sample Output

20

HINT

1<=N,M,K<=5000000,1<=T<=2000

 

---

problem：

求：

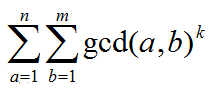
solution：

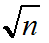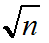预处理出h数组，实现的复杂度

 

推导：

 　　　　　　　　　　　　　　　　　　　　　　

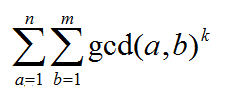
枚举gcd：

　　　　　　　　　　　　 

套路化解：

 　　　　　　　　　　　　

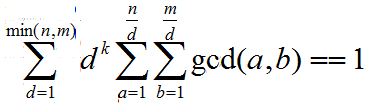
根据公式二：

 　　　　　　　　　　　　

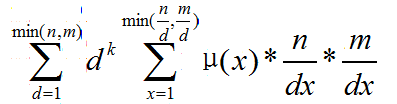
套路枚举dx：

 　　　　　　　　　　　　　

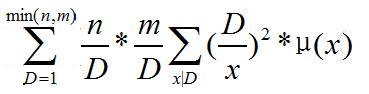
考虑预处理出：   　　　　　　　

　　　　　　　　　　　　　　　　

 

化解一下：　　　　　　　　　

　　　　　　　　　　　　　　

 

 

因为积性函数的约束和也是积性函数，所以h是积性函数：

　　　　　　　　　　　　　　 

线性筛时预处理出h数组：

注意：

如果i%prime[j]==0:则μ(i*prime[j])及以后都为0，不再为h做出贡献，只有D为变。

 　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　

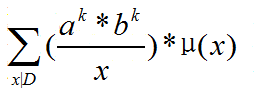
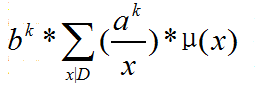
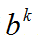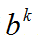我们只需要合并时把h乘上一个即可

否则，根据积性函数性质：h(i*prime[j])=h(i)*h(prime[j]),更新即可。

void getmu()
{
    h[1]=1;
    for(int i=2;i<=N;i++)
    {
        if(!vis[i])
        {
            prime[++cnt]=i;
            g[i]=qpow(k,i);
            h[i]=(g[i]-1+mod)%mod;
        }
        for(int j=1;j<=cnt;j++)
        {
            if(i*prime[j]>N) break;
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) {h[i*prime[j]]=(h[i]*g[prime[j]])%mod;break;}
            h[i*prime[j]]=(h[i]*h[prime[j]])%mod;
        }
    }
    for(int i=1;i<=N;i++) h[i]=(h[i]+h[i-1])%mod;
}

---

 附上代码：

#include<bits/stdc++.h>
using namespace std;
const int N=5e6+12;
const int mod=1e9+7;
int prime[N],cnt,vis[N];
long long h[N],g[N];//注意long long 
long long k;
int n,m;
int qpow(int a,long long b)
{
    long long ans=1;
    while(a)
    {
        if(a&1) ans=ans*b%mod;
        b=b*b%mod;
        a>>=1;
    }
    ans%=mod;
    return ans;
}

void getmu()
{
    h[1]=1;
    for(int i=2;i<=N;i++) 
    {
        if(!vis[i]) 
        {
            prime[++cnt]=i;
            g[i]=qpow(k,i);
            h[i]=(g[i]-1+mod)%mod;
        }
        for(int j=1;j<=cnt;j++) 
        {
            if(i*prime[j]>N) break;
            vis[i*prime[j]]=1;
            if(i%prime[j]==0) {h[i*prime[j]]=(h[i]*g[prime[j]])%mod;break;}
            h[i*prime[j]]=(h[i]*h[prime[j]])%mod;
        }
    }
    for(int i=1;i<=N;i++) h[i]=(h[i]+h[i-1])%mod;
}
int main()
{
    freopen("a.in","r",stdin);
    int T;scanf("%d%d",&T,&k);
    getmu();
    while(T--) 
    {
        scanf("%d%d",&n,&m);
        if(n>m) swap(n,m);
        int pos;
        long long ans=0;
        for(int i=1;i<=n;i=pos+1) 
        {
            pos=min(n/(n/i),m/(m/i));
            long long t=(long long)(n/i)*(m/i)%mod;
            ans=(ans+(long long)t*(h[pos]-h[i-1]+mod)%mod)%mod;
        }
        ans=(ans%mod+mod)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

 

---