BZOJ#2820. YY的GCD

2820: YY的GCD

Time Limit: 10 Sec  Memory Limit: 512 MB
Submit: 2646  Solved: 1454
[Submit][Status][Discuss]

Description

神犇YY虐完数论后给傻×kAc出了一题给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对kAc这种

傻×必然不会了，于是向你来请教……多组输入

Input

第一行一个整数T 表述数据组数接下来T行，每行两个正整数，表示N, M

Output

T行，每行一个整数表示第i组数据的结果

Sample Input

2
10 10
100 100

Sample Output

30
2791

HINT

T = 10000

N, M <= 10000000

---

problem：

给定n,m，求gcd(a,b)为质数的(a,b)的对数，(a<=n,b<=m)

 

---

solution:

 

假设n<m

很容易得到：

　　　　　　　　　  　

 

　　　　　　　　　　　　　

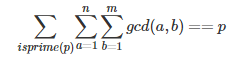
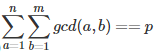
可以化成:

　　　　　　　　　　　　　 

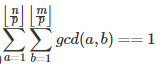
根据μ的性质：　　　　　　　　

　　　　　　　　　　　　

 

→只有当n为1时μ的前缀和为1，否则为0；

 

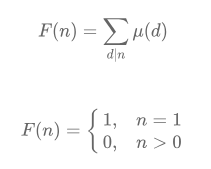
所以 

 

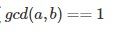
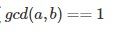
 可以变成:

　　　　　　　　　　　  　

 

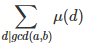
整理一下我们现在的式子：

　　　　　　　　　　　

 

 

d是gcd(a,b)的因子，那么d|a&&d|b

观察：

　　　　　　　　　　　  　

 

 

发现我们会枚举所有的(a,b)然后来确定μ(d)

 

想d会出现多少次，只有(a,b)的gcd是d的倍数，都会加上一个μ(d)

 

意思会加上(n/pd)*(m/pd)次

 

那么我们可以先枚举d：

　　　　　　　　　　　

　　　　　　　　　　　　　　

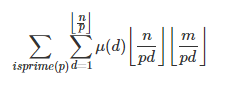
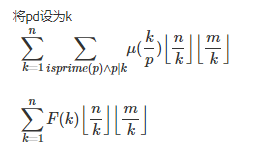
预处理出F(k)

for(int i=1;i<=cnt;i++)
    {  
        int p=prime[i];
        for(int j=1;j*p<=N;j++) F[j*p]+=mu[j];
    }

---

 附上代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e7+12;
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') {x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,m,T;
int used[N],prime[N],mu[N],cnt;
long long F[N];
void getphi()
{
    mu[1]=1;
    for(int i=2;i<=N;i++) 
    {
        if(!used[i]) prime[++cnt]=i,mu[i]=-1;
        for(int j=1;j<=cnt;j++) 
        {
            if(prime[j]*i>N) break;
            used[prime[j]*i]=1;
            if(i%prime[j]==0) {mu[i*prime[j]]=0;break;}
            else mu[i*prime[j]]=-mu[i];
        }
    }
    for(int i=1;i<=cnt;i++) 
    {
        int p=prime[i];
        for(int j=1;j*p<=N;j++) F[j*p]+=mu[j];
    }
    for(int i=1;i<=N;i++) F[i]+=F[i-1];
}
int main()
{
    freopen("a.in","r",stdin);
    getphi();
    T=read();
    while(T--)
    {
        long long ans=0;
        n=read();m=read();
        if(n>m) swap(n,m);
        int j=0;
        for(int i=1;i<=n;i=j+1)
        {
            j=min(n/(n/i),m/(m/i));//因为有可能会有一段相同的(n/i)(m/i)我们就一起算 
            ans+=(F[j]-F[i-1])*(n/i)*(m/i);
        }
        printf("%lld\n",ans);
    }
    return 0;
}

 

---