连通性问题

连通性问题

1. 强连通分量

1.1. 算法解析

在 Tarjan 算法中为每个结点 $u$ 维护了以下几个变量：

$dfn_u$：深度优先搜索遍历时结点 $u$ 被搜索的次序，即 $u$ 的 DFS 序。
$low_u$：不经过 $u$ 的祖先能到达的最小的 $dfn$.

显然，若 $dfn_u = low_u$，则 $u$ 为一个强联通分量的顶端（即最浅的点）。

1.2. 代码

int low[N], dfn[N], idx;
bool vis[N]; // vis[u] 表示节点 u 是否在栈内
stack<int> stk; // 存储所有遍历过的节点，由于每次我们只处理最浅的节点，所以可以利用栈的后进先出的特性

void tarjan(int u)
{
	low[u] = dfn[u] = ++idx;
	stk.push(u), vis[u] = 1;
	for(auto v : g[u])
	{
		if(!dfn[v])
		{
			tarjan(v); // 若没有到达过，继续搜索
			low[u] = min(low[u], low[v]);
		}
		else if(vis[v]) low[u] = min(low[u], dfn[v]); // 若还在栈中，则说明可以从 u 跳到更浅的节点 v，用 v 的 dfn 来更新 low[u] 即可；若不在栈中，说明其联通分量已经被处理过了，无须再处理
	}
	if(low[u] == dfn[u])
	{
		tot++;
		while(h != u) // 不断弹出强联通分量里的数，直到分量内最浅的点 u
		{
			h = stk.top(); stk.pop();
			bel[h] = tot, siz[tot]++, vis[h] = 0;
		}
	}
	return;
}

1.3. 例题

1.3.1 P3119 [USACO15JAN] Grass Cownoisseur G

很有意思的一道题目。

先把强连通分量缩点，然后建两层的分层图，第 $i$ 层表示逆行 $i-1$ 次的情况。
建新图时化边权为点权，将 $(u, v)$ 的边权设为连通分量 $u$ 的节点数。

注意 $(1, 1')$ 之间也要连一条边，因为可能并没有逆行的操作（虽然不加这个也能 AC）。

#include <bits/stdc++.h>
using namespace std;

const int N = 5e5 + 5;

int n, m, x, y, dfn[N], bel[N], low[N], siz[N], tot, h, idx, dis[N], head[N], edges;
bool vis[N];
vector<int> g[N], G[N];
stack<int> stk;

void tarjan(int u)
{
	low[u] = dfn[u] = ++idx;
	stk.push(u), vis[u] = 1;
	for(auto v : g[u])
	{
		if(!dfn[v])
		{
			tarjan(v);
			low[u] = min(low[u], low[v]);
		}
		else if(vis[v]) low[u] = min(low[u], dfn[v]);
	}
	if(low[u] == dfn[u])
	{
		tot++;
		while(h != u)
		{
			h = stk.top(); stk.pop();
			bel[h] = tot, siz[tot]++, vis[h] = 0;
		}
	}
	return;
}

struct edge
{
	int to, nxt, val;
} e[N << 1];

void addedge(int u, int v, int w)
{
	e[++edges] = {v, head[u], w};
	head[u] = edges;
}

void spfa(int s, int t)
{
	queue<int> q;
	memset(vis, 0, sizeof vis);
	memset(dis, 0, sizeof dis);
	q.push(s), vis[s] = 1;
	while(!q.empty())
	{
		int u = q.front(); q.pop();
		vis[u] = 0;
		for(int i = head[u]; i; i = e[i].nxt)
		{
			int v = e[i].to;
			if(dis[v] < dis[u] + e[i].val)
			{
				dis[v] = dis[u] + e[i].val;
				if(!vis[v]) vis[v] = 1, q.push(v);
			}
		}
	}
	cout << dis[t];
	return;
}

int main()
{
	ios :: sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for(int i = 1; i <= m; i++)
	{
		cin >> x >> y;
		g[x].push_back(y);
	}
	for(int i = 1; i <= n; i++)
		if(!dfn[i]) tarjan(i);
	for(int i = 1; i <= tot; i++)
		siz[i + tot] = siz[i];
	for(int u = 1; u <= n; u++)
	for(auto v : g[u])
	{
		if(bel[u] == bel[v]) continue;
		addedge(bel[u], bel[v], siz[bel[u]]);
		addedge(bel[u] + tot, bel[v] + tot, siz[bel[u] + tot]);
		addedge(bel[v], bel[u] + tot, siz[bel[v]]);
	}
	addedge(bel[1], bel[1] + tot, siz[1]);
	spfa(bel[1], bel[1] + tot);
	return 0;
}

2. 边双连通

2.1. 定义

边双连通图：一个无向图中任意两点都存在两条不重合路径。
边双连通分量：无向图中极大的边双连通子图。

性质：

• 没有割边。
• 任意两点之间都由有至少两条边不重复的路径。

2.2. 算法解析

搜索树上的一条边 $(u, v)$ 是割边当且仅当 $low_v > dfn_u$.

求边双连通分量时，找到所有割边，再用另一次 DFS 找出所有边双连通分量。

#include <bits/stdc++.h>
using namespace std;

const int N = 2e6 + 5;

int n, m, u, v, dfn[N], low[N], tot, h, idx, head[N];
vector<int> vet[N];
bool vis[N];

struct edge
{
	int to, nxt, flag;
} e[N << 1];

void addedge(int u, int v)
{
	e[++tot] = {v, head[u], 0}, head[u] = tot;
}

inline void tarjan(int u, int fa)
{
	low[u] = dfn[u] = ++idx;
	for(int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if(!dfn[v])
		{
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if(low[v] > dfn[u]) e[i].flag = e[i ^ 1].flag = 1;
		}
		else if(dfn[v] < dfn[u] && fa != v) low[u] = min(low[u], dfn[v]);
	}
	return;
}

void dfs(int u, int id)
{
	vet[id].push_back(u), vis[u] = 1;
	for(int i = head[u]; i; i = e[i].nxt)
	{
		int v = e[i].to;
		if(!e[i].flag && !vis[v]) dfs(v, id);
	}
	return;
}

int main()
{
	ios :: sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n >> m; tot = 1;
	for(int i = 1; i <= m; i++)
	{
		cin >> u >> v;
		if(u == v) continue;
		addedge(u, v);
		addedge(v, u);
	}
	tot = 0;
	for(int i = 1; i <= n; i++)
		if(!dfn[i]) tarjan(i, 0);
	for(int i = 1; i <= n; i++)
		if(!vis[i]) dfs(i, ++tot);
	cout << tot << '\n';
	for(int i = 1; i <= tot; i++)
	{
		cout << vet[i].size() << ' ';
		for(auto u : vet[i]) cout << u << ' ';
		cout << '\n';
	}
	return 0;
}

3. 点双连通

3.1. 定义

点双连通图：满足以下两个条件之一的无向图。

• 顶点数不超过 $2$.
• 任意两点/边都在一个简单环中。

点双连通分量（V-BCC）：无向图中极大的点双连通子图。

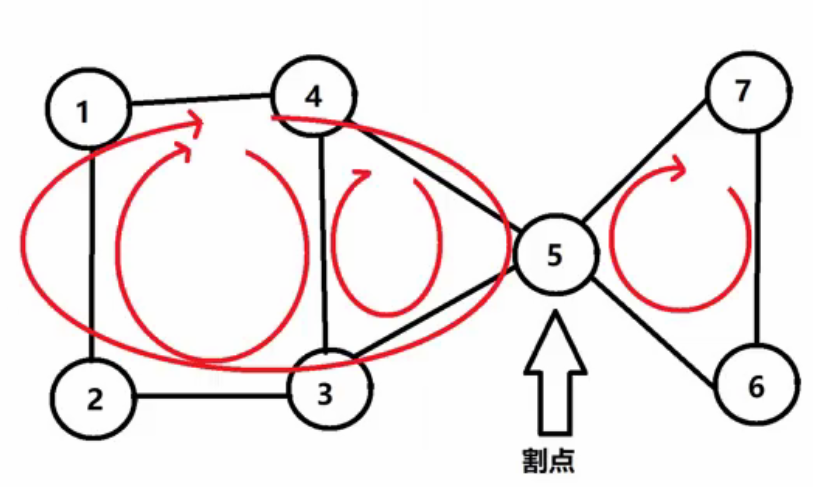
• 割点属于多个点双连通分量，是它们的交界。

3.2. 算法解析

Tarjan，DFS 时把所有边入栈，发现 $low_v \ge dfn_u$ 时发现点双，退栈到 $u$，边上的点构成一个 V-BCC.

#include <bits/stdc++.h>
using namespace std;

const int N = 5e5 + 5;

int n, m, u, v, tot, dfn[N], low[N], idx, bel[N];
bool c[N], r[N];
vector<int> g[N], ans[N];
stack<pair<int, int> > stk;

void tarjan(int u, int fa)
{
	int son = 0;
	low[u] = dfn[u] = ++idx;
	for(auto v : g[u])
	{
		if(!dfn[v])
		{
			stk.push({u, v});
			tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if(low[v] >= dfn[u])
			{
				tot++, c[u] = 1;
				pair<int, int> h;
				do
				{
					h = stk.top(); stk.pop();
					if(bel[h.first] != tot) ans[tot].push_back(h.first), bel[h.first] = tot;
					if(bel[h.second] != tot) ans[tot].push_back(h.second), bel[h.second] = tot;
				} while(h != make_pair(u, v));
			}
			if(!fa) son++;
		}
		else low[u] = min(low[u], dfn[v]);
	}
	if(!fa && son <= 1) c[u] = 0;
	return;
}

int main()
{
	ios :: sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for(int i = 1; i <= m; i++)
	{
		cin >> u >> v;
		if(u == v) continue;
		g[u].push_back(v);
		g[v].push_back(u);		
	}
	for(int i = 1; i <= n; i++)
		if(!dfn[i]) tarjan(i, 0);
	for(int i = 1; i <= n; i++)
		if(!bel[i]) ans[++tot].push_back(i);
	cout << tot << '\n';
	for(int i = 1; i <= tot; i++)
	{
		cout << ans[i].size() << ' ';
		for(auto u : ans[i]) cout << u << ' ';
		cout << '\n';
	}
	return 0;
}

3.3. 圆方树

把原图上的点记为圆点，每个点双连通分量记为方点，所有方点向点双内的所有圆点连边，构成一颗树。

这棵树具有极好的性质，被称为圆方树。