笛卡尔树（Cartesian Tree）

笛卡尔树（Cartesian Tree）

1. 定义

根据序列构造的满足以下性质的树：

• 二叉搜索树性质（BST）：\(key_{ls} \le key_x \le key_{rs}\)，\(key\) 默认为下标。
• 堆性质：\(val_{x} \le val_{ls} \le val_{rs}\).

2. 构造

• 如果有 \(key\) 作为第一关键字，则按 \(key\) 升序排序，否则默认下标为 \(key\)；
• 使用单调栈维护右链，按照 \(key\) 升序的顺序添加节点。
• 加入一个新节点 \(i\) 时，找到右链上第一个 \(val_j \le val_i\) 的节点，将 \(rs_j\) 作为 \(i\) 的左儿子，\(i\) 作为新的 \(rs_j\).

const int N = 1e5 + 5;
int n, root, v[N], fa[N], ls[N], rs[N];
stack<int> stk;

void build()
{
	for(int i = 1; i <= n; i++)
	{
		cin >> v[i];
		while(!stk.empty() && v[stk.top()] > v[i])
			ls[i] = stk.top(), stk.pop();
		fa[i] = (!stk.empty() ? stk.top() : 0);
		if(!fa[i]) root = i;
		if(ls[i]) fa[ls[i]] = i;
		if(fa[i]) rs[fa[i]] = i;
		stk.push(i);
	}
	return;
}

3. 应用

3.1. 求区间最小值（RMQ）

建立小根笛卡尔树，区间 \([a, b]\) 的最小值是 \(val_{\operatorname{LCA}(a, b)}\).

利用 BST 的性质可以快速求 LCA.

复杂度为树的深度，随机数据下为 \(O(n \log n)\).

int find_min(int a, int b)
{
	int lca = root;
	while(lca < a || lca > b)
	{
		if(lca < a) lca = rs[lca];
		if(lca > b) lca = ls[lca];
	}
	return v[lca];
}

3.2. 求最小值范围

给定一个无序序列和一个下标，求对应的值是多大范围内的最小值。

• 建立小根笛卡尔树，下标 \(i\) 对应的区间为 \(i\) 的子树中最左边的点到最右边的点。

3.3. 最大矩形

求下图的最大矩形（\(n \le 10^5\)）：

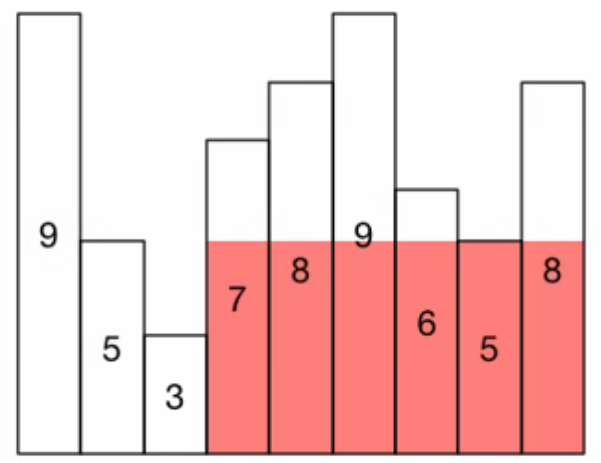
• 建立小根笛卡尔树，每个点的贡献是 \(\text{子树大小} \times \text{深度}\).

4. 例题

4.1. P1350 车的放置

\(f_{i,j}\)：在 \(i\) 的子树中放 \(j\) 个车的方案数。

\(f_{u, i} = \sum_{j=0}^i son_i \times j!\begin{pmatrix}i-1 \\j\end{pmatrix}\begin{pmatrix}w-(i-j) \\j\end{pmatrix}\).

\(son_i = \sum_{j=0}^i (f_{lc, j} \times f_{rc, i-j})\).

在 \(n \times m\) 的矩形中放 \(k\) 个车：\(C_n^k \times C_m^k \times k!\).