Temporal Latent Auto-Encoder: A Method for Probabilistic Multivariate Time Series Forecasting AAAI2021 多变量高维时间序列预测

Temporal Latent Auto-Encoder: A Method for Probabilistic Multivariate Time Series Forecasting AAAI2021 多变量高维时间序列预测

Temporal Latent Auto-Encoder: A Method for Probabilistic Multivariate Time Series Forecasting（TLAE），这篇论文实际上站在2016年的NeurlPS经典论文Temporal Regularized Matrix Factorization for High-dimensional Time Series Prediction (TRMF)的肩膀上提出的，其基本思想来自于TRMF中对时间序列矩阵分解，将高维时间序列矩阵进行分解，得到时间序列在低维隐状态空间(low-dimensional latent state space)的表示(latent representation)。

为什么要对时间序列矩阵进行分解？

1. TRMF论文标题即指出的一个关键的motivation，就是high-dimensional time series，对于高维时间序列的处理目前存在困难
   高维时间序列指的是特征的维度搞，也就是同一时刻有大量的特征（可能从数百~数万）

   • 传统的时间序列建模方式（auto regression）通常是针对单变量(univariate)的时间序列建模；
   • 高维时间序列中，不同的时间序列之间往往存在线性or非线性相关关系；
   • 以RNN,CNN,Transformer为代表的深度学习方法虽然在处理高维变量上展现出不错的精度表现，但是当处理高维时间序列数据时，模型在大规模数据上的处理性能是有待提升的，也就是scalable的问题。再者，时间序列建模中常用的RNN模型本身的建模效率就比较低（TCN则在效率上由较大的优势）。

2. 高维时间序列数据，往往在不同的特征上容易出现缺失值(missing value)，异常值(outlier)的问题。

   • 传统的时间序列建模对缺失值和异常值敏感，一般需要对这些数据问题做专门的与处理工作，而通过矩阵分解可以一定程度上对缺失值等进行弥补，提升模型适应噪声的能力；

3. 高维时间序列数据不同特征序列之间的复杂相关性建模问题。

   • 高维时间序列特征繁多，在时间序列建模中，不仅要考虑数据在时间(temporal)上的相关性，也要提取数据不同特征序列之间的相关性(spatial)；

time series matrix factorization 直接参照related work部分理解

TLAE的主要motivation，也就是现有研究的research gap

1. 提取序列之间的非线性相关性（在latent representation中进行表示）；
2. 现有的基于矩阵分解（matirx factorization, MF）的时间序列建模方法一般是采用交替最小化的求解方法，求解不稳定，容易陷入局部最优。TLAE中试图直接求解，end-to-end的优化方式；

TLAE

点预测 Point prediction

模型结构解析

time series matrix factorization
\(Y \in R^{n \times T}\)；
\(Y = FX\) 其中，\(X \in R^{d \times T}\), \(F \in R^{n \times d}\)；
\(X = F^+ Y\)，\(F^+\)是\(F\)的伪逆；
\(Y=FF^+ Y\)，看到这个公式，其实和autoencoder的思想(Y -> latent representation -> Y)就有些接近了，其中的\(F^+\)相当于encoder把输入Y变成latent represenataion，\(F\)相当于decoder把latent representation重建为Y。
进而，在TLAE中，就是用encoder和decoder作为上面的矩阵\(F^+\)和\(F\)
encoder和decoder可以根据数据来设计，并非传统意义上的矩阵分解，那么就解决了第一个motivation，提取序列之间的非线性相关性。

• encoder的参数设为\(\phi\)，那么就有\(X=g_\phi(Y)\)，\(g\)表示encoder，把原始数据Y映射到低维latent representation \(X\)，也就是\(g:R^n \longrightarrow R^d\)；

• decoder的参数设为\(\theta\)，那么就有\(\hat{Y}=f_\theta(X)\)，\(f\)表示decoder，把latent representation \(X\)进行重建到\(\hat{Y}\)，也就是\(f:R^d \longrightarrow R^n\)，\(d<<n\)；
  下面这个图片是TLATE的模型结构图
  

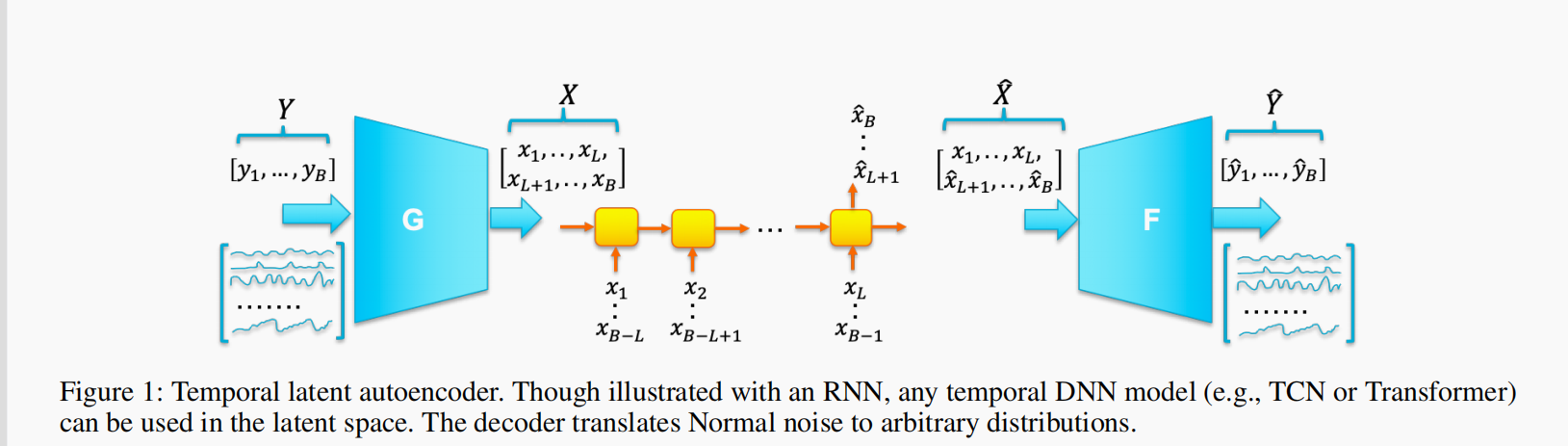
• 模型输入是一个batch的数据\(Y_B=[y_1,...,y_B]\)，\(y_i\)是一个n维向量；

• \(Y_B\)经过encoder映射到隐空间得到latent representation \(X=[x_1,...,x_B]\)，\(x_i\)是一个d维向量，也就是\(X=g_\phi(Y)\)；

• encoder和decoder中间加了一个时间序列建模层middle layer（LSTM, GRU, TCN, Transformer均可）,这里加上这个是为了让latent representation包含序列的时序信息；

  • 在时序建模层中需要有一个滞后时长\(L\)，也就是捕获前\(L\)个时刻的时序信息；
  • \([x_1,...,x_L]\)没法在这个middle layer上建模，所以直接保留下来；
  • \([x_{L+1},...,x_{B}]\)可以在这个middle layer上进行重建，也就是让重构的\([\hat{x}_{L+1},...,\hat{x}_{B}]\)中的每个都包含前\(L\)个时刻的信息；
    • \([x_1,...,x_L]\)输入到LSTM得到最后一个hidden state作为\(\hat{x}_{L+1}\);
    • 以此类推，一直到最后\([x_{B-L},...,x_{B-1}]\)输入LSTM得到最后一个hidden state作为\(\hat{x}_B\)；
    • \([\hat{x}_{L+1},...,\hat{x}_{B}]\)中每个元素都包含了前\(L\)个时刻的信息；
    • 对于\([\hat{x}_{L+1},...,\hat{x}_{B}]\)实际上LSTM做了这么一件事\(\hat{x}_{i+1}=h_W(x_{i-L+1},...,x_i)\)，其中W是middle layer的参数，这里就是LSTM的参数；
  • 经过这个middle layer (LSTM)之后，latent representation \(X\)变成了\(\hat{X}\)。\(\hat{X}\)包含两个部分：
    • 没有经过LSTM重构的\([x_1,...,x_L]\)，每个元素不包含时序信息；
    • 经过LSTM重构的\([\hat{x}_{L+1},...,\hat{B}]\)，每个元素包含前\(L\)个时刻的时序信息，相当于用前\(L\)个时刻的信息对下一个时刻做了预测；
  • 将\(\hat{X}\)输入到decoder，在重构出\(\hat{Y}\)，完成autoencoder的使命，让\(\hat{Y}\)尽可能接近原始数据\(Y\)；
    • \(\hat{Y}\)也可以分为两个部分：
      • 第1部分是由\([x_1,...,x_L]\)重构而来的，也就是当\(i \in [1, L]\)，\(\hat{y_i}=f_\theta \circ g_\phi(y_i)\)
      • 第2部分是由\([\hat{x}_{L+1},...,\hat{B}]\)重构而来的，也就是当\(i \in [L+1, B]\)，\(\hat{y_i+1}=f_\theta \circ h_W \circ g_\phi(y_{i-L+1},...,y_i)\)；

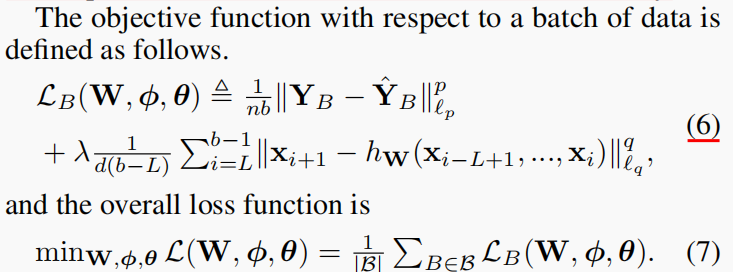
公式(6)是一个batch上的损失函数，公式(7)是整体损失函数，直接看公式(6)即可

• 公式(6)的前半部分是autoencoder的常规操作，要求输出充分还原输入，因而最小化两者之差的范数；
• 公式(6)的后半部分是正则项，要求middle layer (LSTM)充分起到提取latent representation之间的时序预测关系的效果，也就是对于\(i \in [L+1, B]\)，LSTM的最后一个隐藏状态\(\hat{x}_{i+1}\)要充分接近\(x_{i+1}\);

模型预测

现有的基于MF的时间序列预测，一般需要把预测得到的latent representation再乘以矩阵F进行还原，但是TLAE不需要这样做，直接根据auto encoder还原的结果就可以，主要原因在于中间的middle layer （LSTM）。
试想我们要预测\(T+1\)时刻的数据\(\hat{y}_{T+1}\)，直接把\([y_{T-L+1},...,y_{T}]\)输入这个autoencoder，经过encoder转换为latent representation \([x_{T-L+1},...,x_{T}]\)，再把这个latent representation输入到middle layer得到\(\hat{x}_{T+1}=h_W(x_{T-L+1},...,x_{T})\)，这里的\(\hat{x}_{T+1}\)已经包含了前\(L\)个时刻的数据信息，再把它输入到decoder，得到的就是我们要的预测值\(\hat{y}_{T+1}\)。

概率预测 Probabilistic prediction

点预测看懂了，这里就很简单，两个基本假设，从这两个假设出发

• 时间序列预测的条件概率假设
• autoencoder得到的隐空间维度之间的正交性假设

参考链接

latent representation
An implementation of TLAE