Jump Point Search(JPS)算法总结与实现(附Demo)
关于这篇文章
第一次翻阅A星算法的文章,是为了弄清楚A星在游戏开发中的地位。当是在脑海中没有形成它的算法模型,也苦于没有一个自定义轨迹且又能展示每一步的细节的demo,于是自己动手写了一个测试demo。后来又因为效率的问题接触到了JPS,于是又实现了一版JPS的逻辑,后分别整理成文章发布。
这期间大约经历了一个月时间,这段时间有很多人给我讲,这些内容网上有很多,没必要费那么大的功夫。
但~ 我觉得,做一个领域的研究要有锱铢必较的心态,这才是做程序开发本该有的素养。
从市场的角度来想,这个行业会不断的有新鲜血液注入,所以翻阅的需求就一直存在,能否被看到可能只是一个概率的问题。
但~ 在其他方面,我也收获了很多,比如个人网站的建立,博客的编辑发布,以及找到了适合自己写博文的工具链……
关于Jump Point Search
Jps,Jump Point Search,跳点搜索,也有人称之为“拐点寻路”。Jps可追溯到2011年,由两位澳大利亚的教授提出,有兴趣的可以翻阅一下原作者论文,github Harabor, Daniel Damir, and Alban Grastien. "Online Graph Pruning for Pathfinding On Grid Maps." AAAI. 2011.
Jps在A Star算法模型的基础之上,优化了搜索后继节点的操作。A星的处理是把周边能搜索到的格子,加进OpenList,然后在OpenList中弹出最小值……。JPS也是这样的操作,但相对于A星来说,JPS操作OpenList的次数很少,它会先用一种更高效的方法来搜索需要加进OpenList的点,然后在OpenList中弹出最小值……
先看两个图来对A星和JPS的差异有个简单的认识。

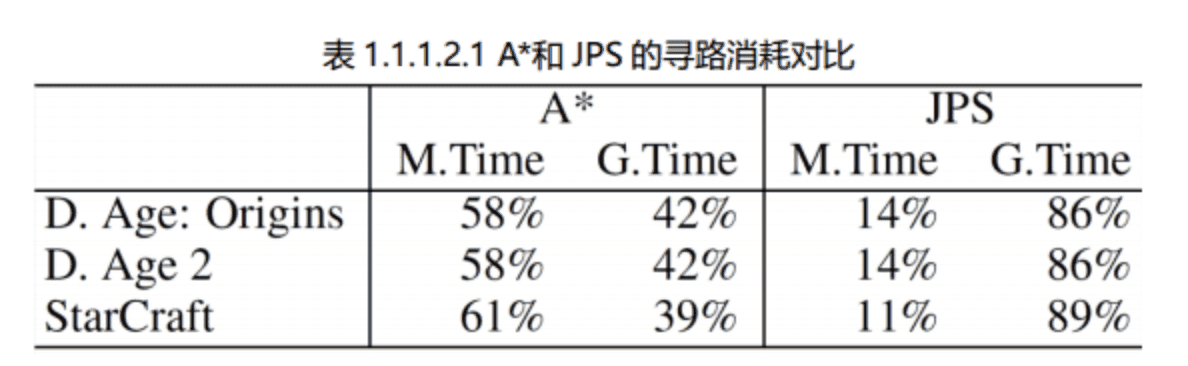
M.Time 表示操作 openset 和 closedset 的时间
G.Time 表示搜索后继节点的时间
A*大约有 58%的时间在操作 openset 和 closedset,42%时间在搜索后继节点
JPS 大约 14%时间在操作 openset 和 closedset,86%时间在搜索后继节点。
到这里我们已经知道如果,JPS保留了一些A星的算法模型,所以,在理解A星算法模型的基础之上,再来阅读JPS的算法模型,可能会事半功倍。
如果你还不理解A星的算法模型,可以是这翻阅以下几个链接。
维基百科-A* search algorithm
A星寻路算法介绍-莫水千流-博客园
A Star Algorithm总结与实现
A Star算法总结与实现(附Demo)
概念
点的容器
寻路过程中需要保存有效点的集合,分为可探索点集合openList,已探索点集合closeList
路径权值
同A星的概念 g为起点经过其他点到当前点的代价和,h为到目标点的代价,f为当前点的与起点终点间价值的和即f=g+h。
强迫邻居
节点 x 的8个邻居中有障碍,且 x 的父节点 p 经过x 到达 n 的距离代价比不经过 x 到达的 n 的任意路径的距离代价小,则称 n 是 x 的强迫邻居。
乍一看觉得这个定义有点难理解,举一个简单的栗子,下面的逻辑是代码逻辑判定强迫linkup。
在JPS的搜索中,强迫邻居的判断可以分为两种,一是水平搜索方向上,一是对角搜索方向上。
先介绍水平方向上,如下图(7,10)为起点,向右进行横向搜索。当搜索到(9,10)时,检测到(9,11)是障碍点,(10,11)是可行走点,因此(9,10)会被认定为跳跃点,而(10,11)是(9,10)的强迫邻居。
同理,(9,9)是障碍点,(10,9)是可行走点,因此(9,10)会被认为是跳跃点,(10,9)是(9,10)的强迫邻居。

再就是对角方向上的搜索,(7,10)是搜索起点,对右下角的(8,9)进行判断。
(8,9)左侧(7,9)是障碍点且(8,8)是可行走点的情况下,若(7,8)是可行走点,则认为(7,8)就是强迫邻居。
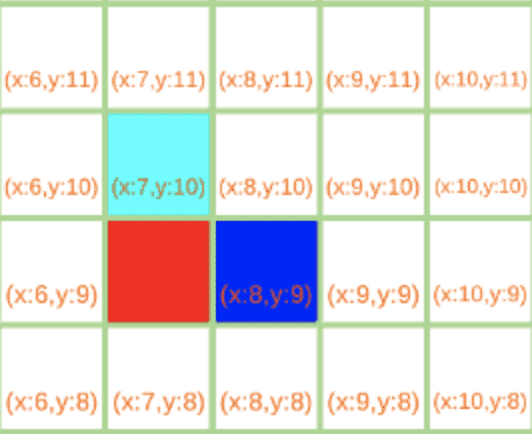
同理,若(8,10)是障碍点,(9,9)是可行走点的情况下,如果(9,10)是可行走点 则认为(9,10)是强迫邻居。

简而言之,其实强迫邻居的判断就是两种情况,一是横向判断,一是对角判断。
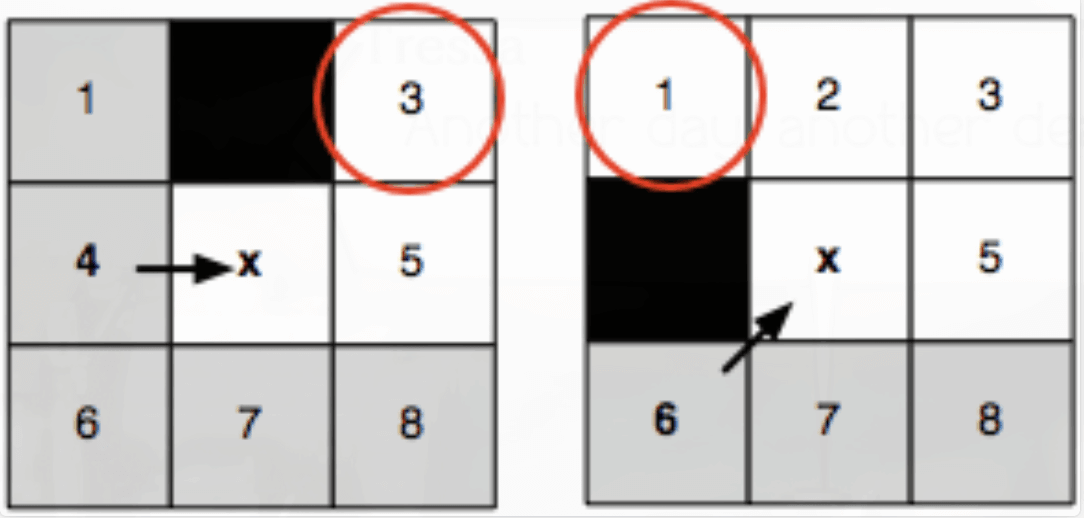
跳跃点
- 如果点 y 是起点或目标点,则 y 是跳点
- -如果 y 有邻居且是强迫邻居则 y 是跳点, 从上文强迫邻居的定义来看 neighbor 是强迫邻居,current 是跳点,二者的关系是伴生的,-
- 如果 parent到 y 是对角线移动,并且 y 经过水平或垂直方向移动可以到达跳点,则 y 是跳点。
通俗一点的讲就是在路径上改变移动方向的点就是跳跃点。
JPS寻路算法的运行轨迹
以浅蓝色为起点,深蓝色为终点。有透明度的格子代表该格子被搜索过(有可能会被重复搜索),有FGH值的格子代表有跳跃点(终点会被认为是一个特殊的跳跃点)。
起点与终点之间,无障碍情况下

起点与终点之间,有直线障碍的情况下
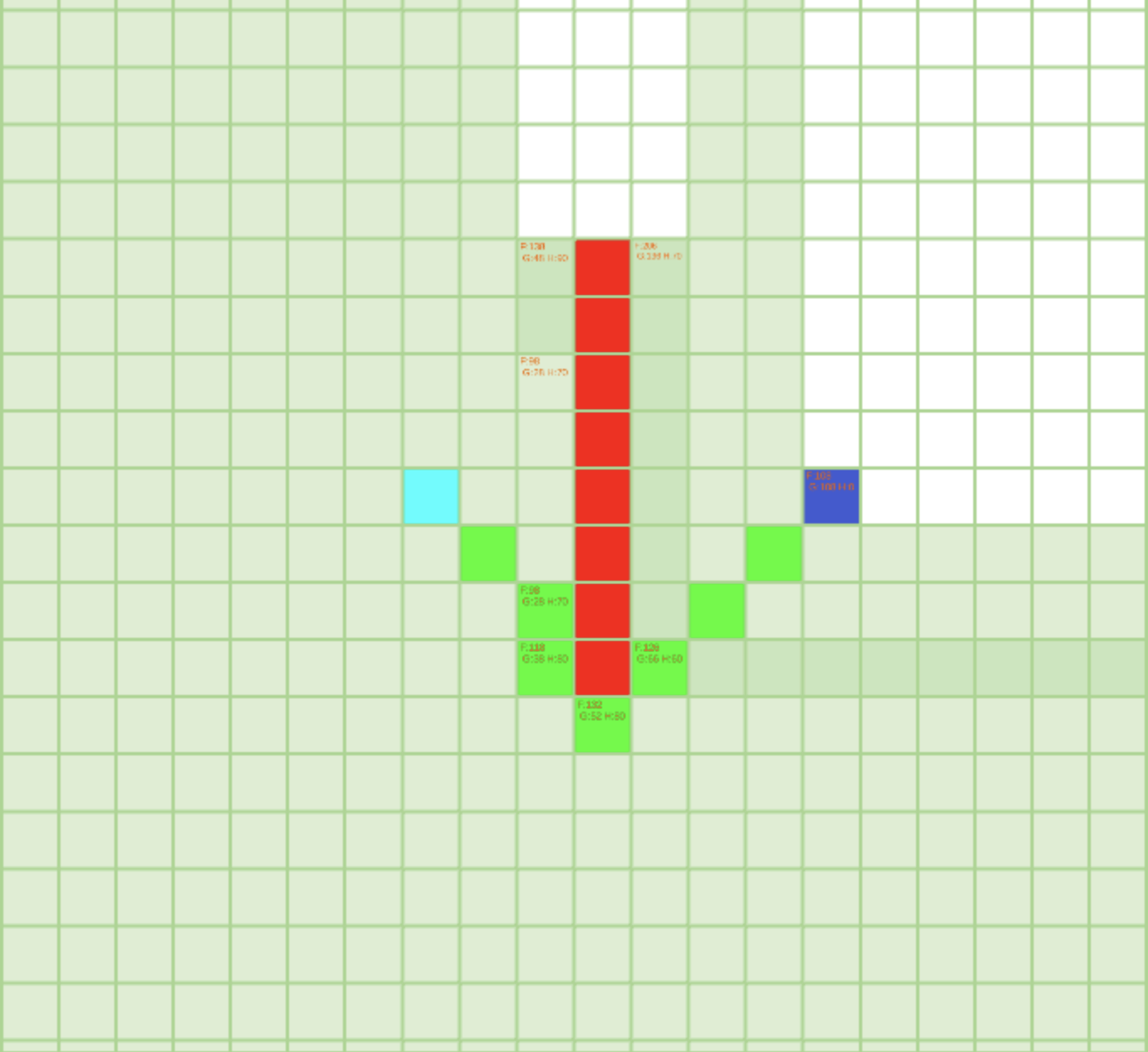
起点与终点之间有U型障碍的情况下
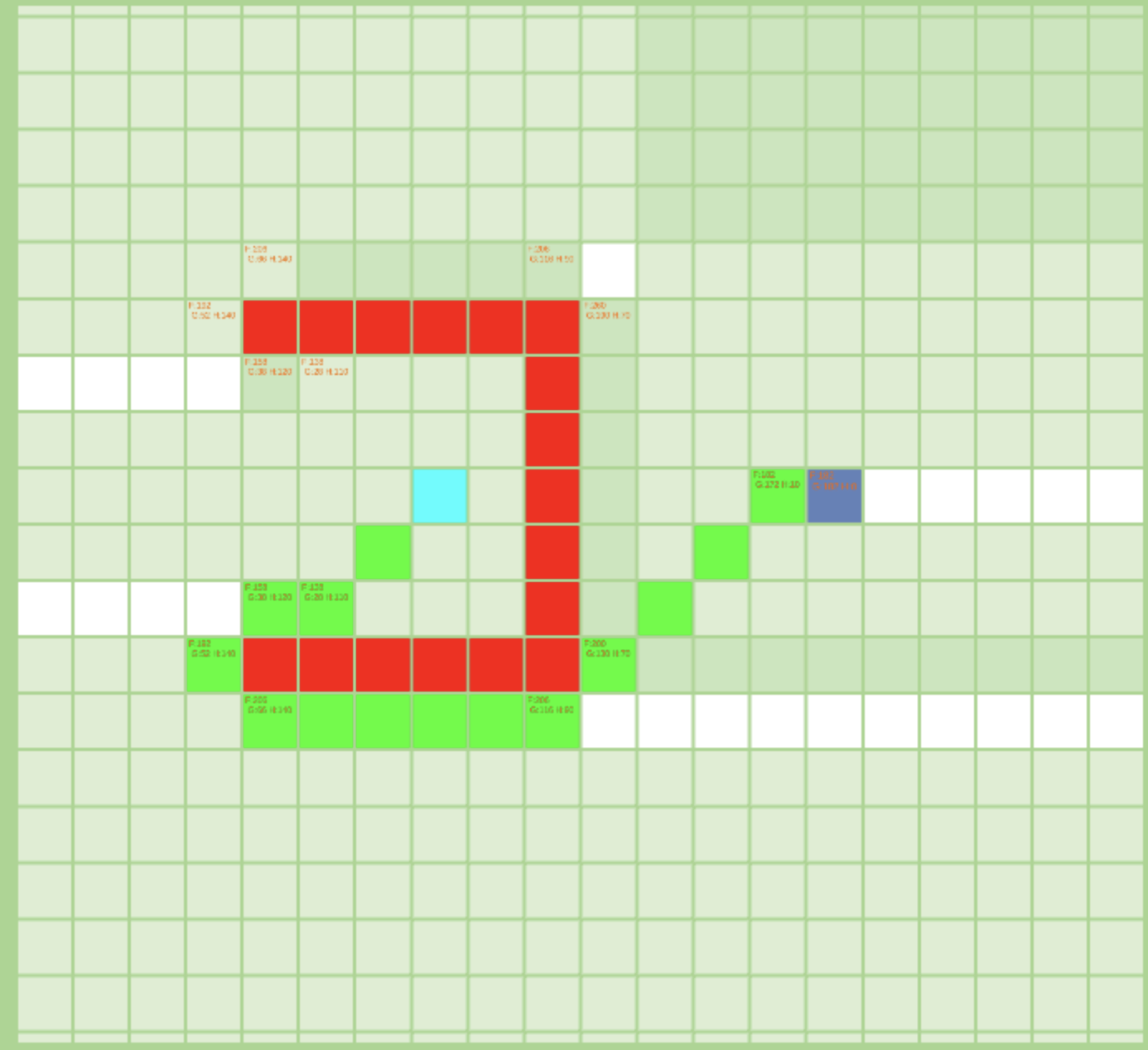
A星与JPS的轨迹动图
大致的流程应该就是这样
A星的轨迹动图

JPS的轨迹动图
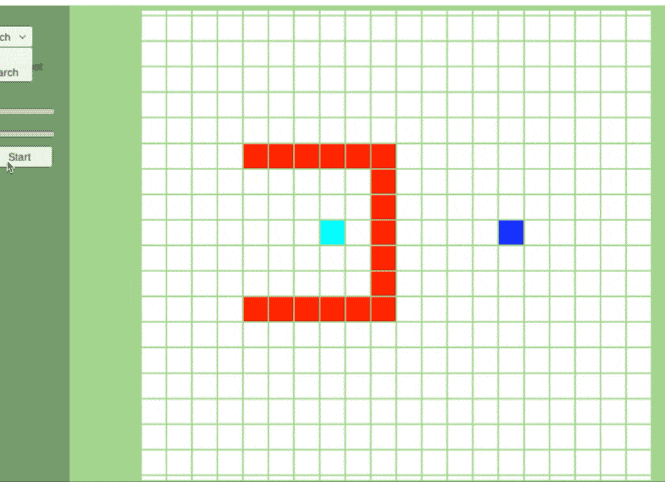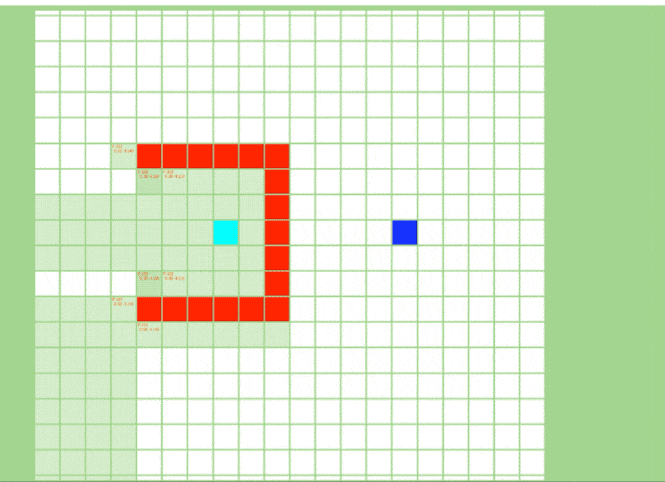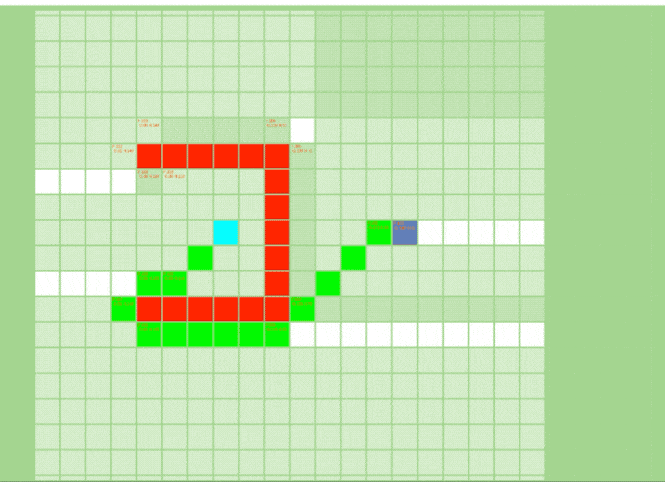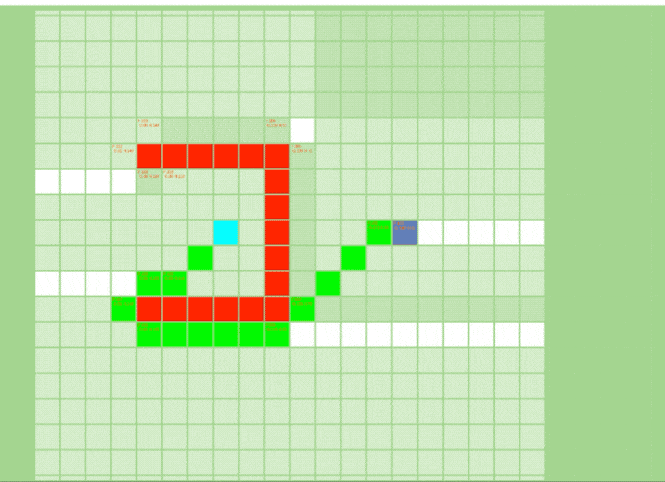
JPS算法里只有跳点才会被加入openlist里,排除了大量不必要的点,最后找出来的最短路径也是由跳点组成。这也是 JPS/JPS+ 高效的主要原因。
伪代码算法
横向纵向的格子的单位消耗为10,对角单位消耗为14。
定义一个OpenList,用于存储和搜索当前最小值的格子。
定义一个CloseList,用于标记已经处理过的格子,以防止重复搜索。
def 获取邻居点
if 当前点是起点
返回当前点九宫格内的非障碍点
elseif 当前点与父节点是对角向
判断并添加相对位置右方的邻居点
判断并添加相对位置下方的邻居点
判断并添加相对位置对角的邻居点
判断并添加相对位置左下角的强迫邻居
判断并添加相对位置左上角的强迫邻居
elseif 当前点与其父节点是横向
判断并添加相对位置右方的邻居点
判断并添加相对位置上方的强迫邻居
判断并添加相对位置下方的强迫邻居
elseif 当前点与父节点是纵向
同横向逻辑,判断并处理下方,左右向强迫邻居
def 递归寻找跳跃点
if 传入点是终点
返回终点
if 传入朝向是对角向
if 传入点存在强迫邻居
返回此传入点
if (递归寻找跳跃点 传入点:横向+1 朝向:横向)结果不为空
返回此传入点
if (递归寻找跳跃点 传入点:纵向+1 朝向:纵向)结果不为空
返回此传入点
elseif 横向
if 上下方有强迫邻居
返回此传入点
elseif 纵向
if 左右方有强迫邻居
返回此传入点
返回 递归寻找跳跃点 传入点:横向+1,纵向+1 朝向 对角
def Main
起点加进OpenList中
While(OpenList.Count > 0):
从OpenList中取出F值最小的点并设置为当前点
把当前点加进CloseList
邻居点s = 获取邻居点(当前点)
for 邻居点s
跳跃点 = 递归寻找跳跃点(邻居点)
if 跳跃点不再CloseList中
计算并设置当前点与跳跃点的G值
计算并设置当前点与跳跃点的H值
计算并设置跳跃点的F值
将当前点设置为跳跃点的父节点
如果邻居点在OpenList中
计算当前值的G与该邻居点的G值
如果G值比该邻居点的G值小
将当前点设置为该邻居点的父节点
更新该邻居点的GF值
若不在
计算并设置当前点与该邻居点的G值
计算并设置当前点与该邻居点的H值
计算并设置该邻居点的F值
将当前点设置为该邻居点的父节
代码相关
获取邻居点
public List<Point> GetNeighbors(Point point)
{
var points = new List<Point>();
Point parent = point.ParentPoint;
if (parent == null)
{
//获取此点的邻居
//起点则parent点为null,遍历邻居非障碍点加入。
for (int x = -1; x <= 1; x++)
{
for (int y = -1; y <= 1; y++)
{
if (x == 0 && y == 0)
continue;
if (IsWalkable(x + point.X, y + point.Y))
{
points.Add(new Point(x + point.X, y + point.Y));
}
}
}
return points;
}
//非起点邻居点判断
int xDirection = Mathf.Clamp(point.X - parent.X, -1, 1);
int yDirection = Mathf.Clamp(point.Y - parent.Y, -1, 1);
if (xDirection != 0 && yDirection != 0)
{
//对角方向
bool neighbourForward =IsWalkable(point.X, point.Y + yDirection);
bool neighbourRight =IsWalkable(point.X + xDirection, point.Y);
bool neighbourLeft =IsWalkable(point.X - xDirection, point.Y);
bool neighbourBack =IsWalkable(point.X, point.Y - yDirection);
if (neighbourForward)
{
points.Add(new Point(point.X, point.Y + yDirection));
}
if (neighbourRight)
{
points.Add(new Point(point.X + xDirection, point.Y));
}
if ((neighbourForward || neighbourRight) && IsWalkable(point.X + xDirection, point.Y + yDirection))
{
points.Add(new Point(point.X + xDirection, point.Y + yDirection));
}
//强迫邻居的处理
if (!neighbourLeft && neighbourForward)
{
if (IsWalkable(point.X - xDirection, point.Y + yDirection))
{
points.Add(new Point(point.X - xDirection, point.Y + yDirection));
}
}
if (!neighbourBack && neighbourRight)
{
if (IsWalkable(point.X + xDirection, point.Y - yDirection))
{
points.Add(new Point(point.X + xDirection, point.Y - yDirection));
}
}
}
else
{
if (xDirection == 0)
{
//纵向
if (IsWalkable(point.X, point.Y + yDirection))
{
points.Add(new Point(point.X, point.Y + yDirection));
//强迫邻居
if (!IsWalkable(point.X + 1, point.Y) &&IsWalkable(point.X + 1, point.Y + yDirection))
{
points.Add(new Point(point.X + 1, point.Y + yDirection));
}
if (!IsWalkable(point.X - 1, point.Y) &&IsWalkable(point.X - 1, point.Y + yDirection))
{
points.Add(new Point(point.X - 1, point.Y + yDirection));
}
}
}
else
{
//横向
if (IsWalkable(point.X + xDirection, point.Y))
{
points.Add(new Point(point.X, point.Y + yDirection));
//强迫邻居
if (!IsWalkable(point.X, point.Y + 1) &&IsWalkable(point.X + xDirection, point.Y + 1))
{
points.Add(new Point(point.X + xDirection, point.Y + 1));
}
if (!IsWalkable(point.X, point.Y - 1) &&IsWalkable(point.X + xDirection, point.Y - 1))
{
points.Add(new Point(point.X + xDirection, point.Y - 1));
}
}
}
}
return points;
}
递归跳跃
private Point Jump(int curPosx, int curPosY, int xDirection, int yDirection, int depth, Point end)
{
if (!IsWalkable(curPosx, curPosY))
return null;
CallSearch(curPosx, curPosY);
//递归最大深度 || 搜索到终点
if (depth == 0 || (end.X == curPosx && end.Y == curPosY))
return new Point(curPosx, curPosY);
//对角向
if (xDirection != 0 && yDirection != 0)
{
if ((IsWalkable(curPosx + xDirection, curPosY - yDirection) && !IsWalkable(curPosx, curPosY - yDirection)) || (IsWalkable(curPosx - xDirection, curPosY + yDirection) && !IsWalkable(curPosx - xDirection, curPosY)))
{
return new Point(curPosx, curPosY);
}
//横向递归寻找强迫邻居
if (Jump(curPosx + xDirection, curPosY, xDirection, 0, depth - 1, end) != null)
{
return new Point(curPosx, curPosY);
}
//纵向向递归寻找强迫邻居
if (Jump(curPosx, curPosY + yDirection, 0, yDirection, depth - 1, end) != null)
{
return new Point(curPosx, curPosY);
}
}
else if (xDirection != 0)
{
//横向
if ((IsWalkable(curPosx + xDirection, curPosY + 1) && !IsWalkable(curPosx, curPosY + 1)) || (IsWalkable(curPosx + xDirection, curPosY - 1) && !IsWalkable(curPosx, curPosY - 1)))
{
return new Point(curPosx, curPosY);
}
}
else if (yDirection != 0)
{
//纵向
if ((IsWalkable(curPosx + 1, curPosY + yDirection) && !IsWalkable(curPosx + 1, curPosY)) || (IsWalkable(curPosx - 1, curPosY + yDirection) && !IsWalkable(curPosx - 1, curPosY)))
{
return new Point(curPosx, curPosY);
}
}
return Jump(curPosx + xDirection, curPosY + yDirection, xDirection, yDirection, depth - 1, end);
}
计算G,H值
protected int CalcG(Point start, Point point)
{
int distX = Math.Abs(point.X - start.X);
int distY = Math.Abs(point.Y - start.Y);
int G = 0;
if (distX > distY)
G = 14 * distY + 10 * (distX - distY);
else
G = 14 * distX + 10 * (distY - distX);
int parentG = point.ParentPoint != null ? point.ParentPoint.G : 0;
return G + parentG;
}
protected int CalcH(Point end, Point point)
{
int step = Math.Abs(point.X - end.X) + Math.Abs(point.Y - end.Y);
return step * 10;
}
传送门
参考与引用
posted on 2020-08-12 23:41 ThisIsRone 阅读(4153) 评论(0) 收藏 举报


 浙公网安备 33010602011771号
浙公网安备 33010602011771号