闵可夫斯基和

概述

对于两个点集 \(A,B\) 来说，把其中的每一个点都看做是对应向量，则这两个集合的闵可夫斯基和定义为 \(C=\{ a+b|a\in A,b\in B \}\)。

凸包的闵可夫斯基和

考虑 \(C\) 为凸包 \(A,B\) 的闵可夫斯基和，那么 \(C\) 的大小应该为 \(|A||B|\)，但是如果考虑 \(C\) 的凸包，那么点数应该是 \(O(|A|+|B|)\) 的。

如图：

至于为什么是这样，我们以上凸壳为例，考虑两个上凸壳的闵可夫斯基和其实是两个上凸壳的归并排序，

如图：

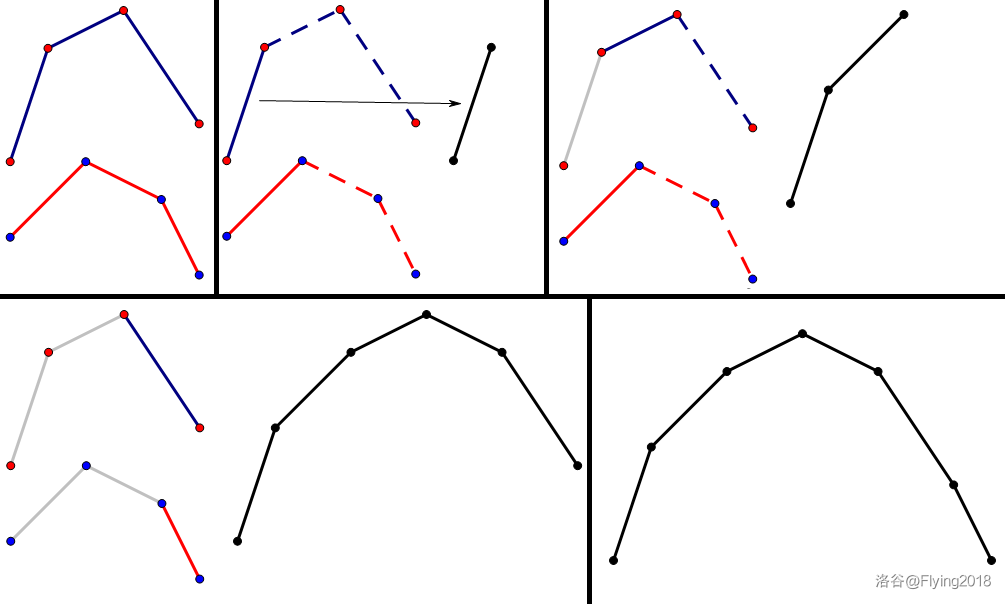
易发现最终凸包上的边都是原来的边，这一点就足以充分说明上面的结论。

所以两个凸包的闵可夫斯基和可以做到 \(O(size)\)。利用类似归并排序即可。具体实现中，我们考虑用一个数组表示一个凸壳，\(a_i\) 表示横坐标为 \(i\) 时凸壳上对应点的纵坐标。

注意到一个凸壳相当于是若干一次函数的复合，则两个上凸壳的合并相当于它们做 \((\max,+)\) 卷积，即加起来的结果取 \(\max\)。这是因为我们考虑 \((\max,+)\) 卷积的形式：

\[c_k=\max\limits_{i+j=k}\{ a_i+b_j \} \]

如果把 \(i,j\) 看做横坐标，把 \(a_i,b_j\) 看做两个凸壳的纵坐标，那么这和 \(C=A+B\) 的定义不谋而合，在 \(C\) 中选的那些最优的点一定构成一个凸壳，而这个凸壳就是我们合并得到的凸壳。

同样的，取 \(\min\) 就是做 \((\min,+)\) 卷积。

闵可夫斯基和与 wqs 二分

wqs 二分可以在 \(O(n\log n)\) 的时间复杂度内求出某一个点值的最优值，但是如果我们的询问变成所有的横坐标，该怎么做？

考虑 wqs 二分的一个经典问题：给定长度为 \(n\) 的序列 \(a_i\)，要求对于每个 \(k=1,2,\cdots,n\)，恰好选出 \(k\) 个不相交的子区间，最大化所有不相交子区间内权值和的和。

显然这个问题可以构建一个费用流模型，如图：

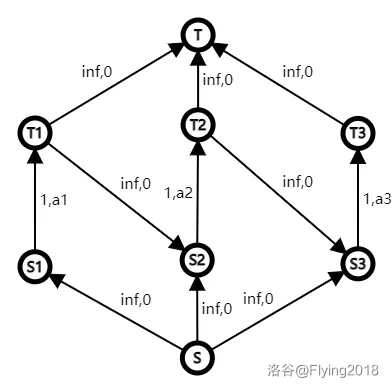
所以这是一个凸函数，可以用 wqs 二分来解决单个值的问题。考虑加强版的问题。

首先考虑一个 DP，设 \(f_{l,r,k,0/1,0/1}\) 表示 \([l,r]\) 中选 \(k\) 个区间，左端点有没有被覆盖，右端点有没有被覆盖。加上后两维的原因是可以合并相邻的两个区间。

考虑这个函数显然关于 \(k\) 是一个凸函数，所以我们任意去一个分界点，总可以在 \(r-l\) 的时间内求出。考虑闵可夫斯基和类似于归并，我们可以取分界点为区间中点，类似分治，求出答案。