牛客算法周周练16D Rinne Loves Dynamic Graph（分层图最短路 + 堆优化dijkstra）

题目大意：

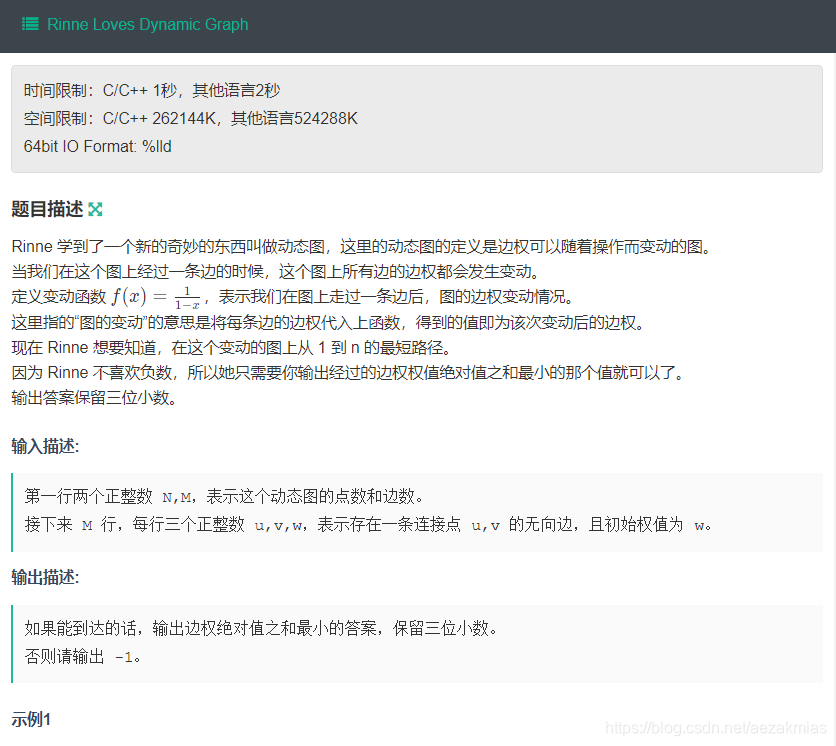
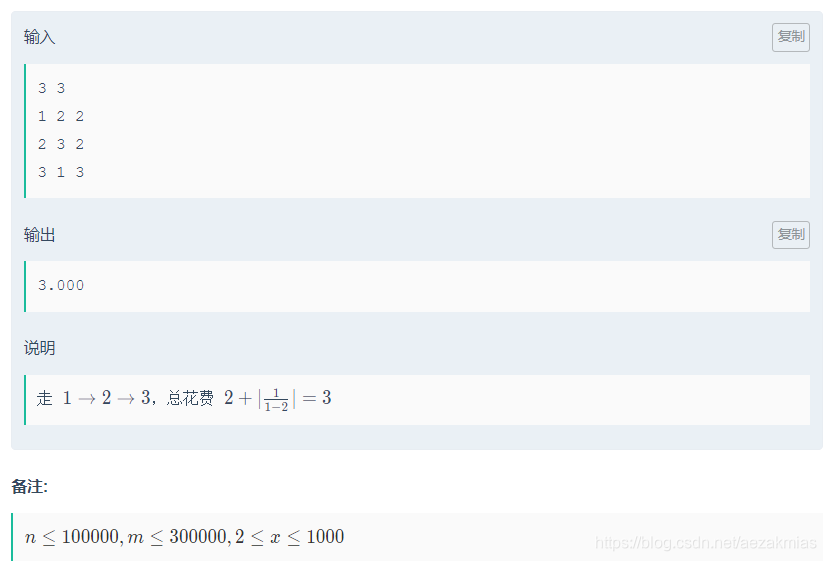
先输入节点数和边数，然后对应每条边输入起点位置和终点位置，再输入权值建图，这张图是个动态图，既每走一步，图中所有节点的权值都会发生变化，这个变化是1 / （1 - x）先观察这个函数，多代几次数，发现这是一个迭代函数，变化三次后又会回到原来的 x，这样可以根据题意分三层建图，每层只能通往更高层的位置，而第三层的下一步又会回到第一层，就可以实现动态图了，用一个邻接表存图，存图的时候权值取绝对值（题目要求）之后跑一个堆优化的迪杰斯特拉，讨论每一层的最短路即可得出答案。AC代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
using namespace std;
const int mod = 1e9 + 7;
const int N = 1e5 + 50;
const int inf = 0x3f3f3f3f;
typedef long long ll;
typedef pair<int, int> pii;
struct edge { int to, next; double val; }e[18 * N];
struct pr
{
	int d;	
	double val;
	bool operator < (const pr &t)const
	{
		return val > t.val;
	}
};
int head[3 * N], vis[3 * N], n, m, cnt = 0;
double dis[3 * N];
void add(int u, int v, double w)
{
	e[++cnt].to = v;
	e[cnt].val = w;
	e[cnt].next = head[u];
	head[u] = cnt;
}
void dijkstra(int s)
{
	memset(vis, 0, sizeof vis);
	for (int i = 1; i <= 3 * n; i ++)
	  dis[i] = inf;
	dis[1] = 0;
	priority_queue<pr > q;
	q.push({1, 0});
	while (!q.empty())
	{
		pr t = q.top();
		q.pop();
		if (vis[t.d])  continue;
		vis[t.d] = 1;
		for (int i = head[t.d]; i; i = e[i].next)
		{
			int v = e[i].to;
			if (t.val + e[i].val < dis[v])
			{
				dis[v] = t.val + e[i].val;
				q.push({v, dis[v]});
			}
		}
	}
}
int main()
{
	int u, v;
	double w;
	memset(head, 0, sizeof head);
	cin >> n >> m;
	for (int i = 1; i <= m; i ++)
	{
		cin >> u >> v >> w;
		add(u, v + n, fabs(w));
		add(v, u + n, fabs(w));
		w = (1.0 / (1 - w));
		add(u + n, v + 2 * n, fabs(w));
		add(v + n, u + 2 * n, fabs(w));
		w = (1.0 / (1 - w));
		add(u + 2 * n, v, fabs(w));
		add(v + 2 * n, u, fabs(w));
	}
	dijkstra(1);
	double ans = dis[n];
	for (int i = 0; i <= 2; i ++)
	  ans = min(ans, dis[n + i * n]);
	if (ans == inf)
	{
		cout << -1 << endl;
		return 0;
	}
	printf("%.3lf\n", ans);
	return 0;
}