从“四人过桥”到“N人过桥”

手电筒—过桥问题

四人过桥+一个手电筒

解析

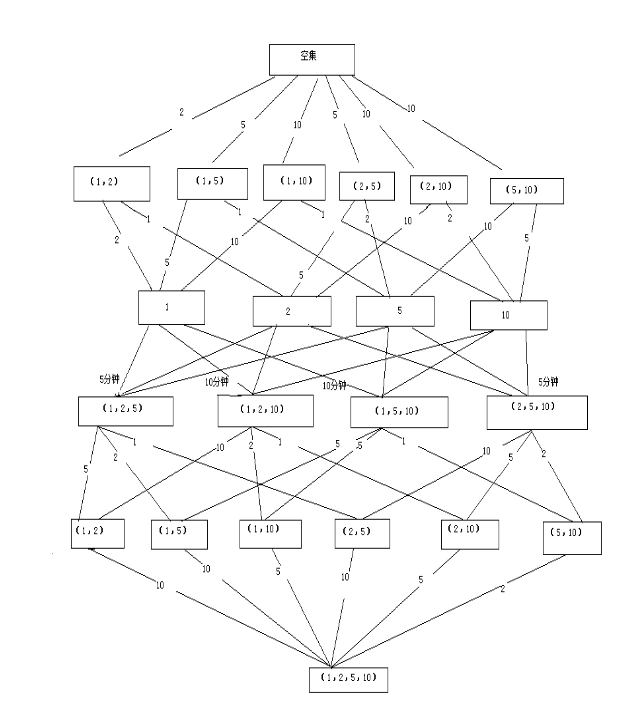
• 考虑图论的方法，以桥的另一边有哪几个人为状态建点，按照规则连边并加上权值，然后从对岸没有人的状态点到四个人都在对岸的状态点跑最短路，最短路长度即为答案
• 我这里的建点和建图都有些麻烦而且不易推广， wyxdrqc 大佬说可以用一个四位二进制数来表示状态， x 号人在对岸则他对应的第 x 位为 1 ，否则为 0 ，这里没有尝试代码实现，只有建图比较麻烦的代码，而且最短路用的 Floyd 算法

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
int num,c[5],e[105][105],p[105],q[105][105],t[105][105],d[5][5][105];
void build()
{
	for(int i=1;i<=3;i++)
	  for(int j=i+1;j<=4;j++)
	  {
	  	num++;
	  	q[num][++p[num]]=i;
	  	q[num][++p[num]]=j;
	  	d[1][i][++t[1][i]]=num;
	  	d[1][j][++t[1][j]]=num;
	  	e[0][num]=max(c[i],c[j]);
	  }
	for(int i=1;i<=4;i++)
	{
		num++;
		q[num][++p[num]]=i;
		d[2][i][++t[2][i]]=num;
		for(int j=1;j<=t[1][i];j++)
		  for(int k=1;k<=p[d[1][i][j]];k++)
			if(q[d[1][i][j]][k]!=i) e[d[1][i][j]][num]=c[q[d[1][i][j]][k]];
	}
	for(int i=1;i<=2;i++)
	  for(int j=i+1;j<=3;j++)
	    for(int k=j+1;k<=4;k++)
	    {
	    	num++;
	    	q[num][++p[num]]=i;
	    	q[num][++p[num]]=j;
	    	q[num][++p[num]]=k;
	    	d[3][i][++t[3][i]]=num;
	    	d[3][j][++t[3][j]]=num;
	    	d[3][k][++t[3][k]]=num;
	    	for(int l=1;l<=t[2][i];l++) e[d[2][i][l]][num]=max(c[j],c[k]);
	    	for(int l=1;l<=t[2][j];l++) e[d[2][j][l]][num]=max(c[i],c[k]);
	    	for(int l=1;l<=t[2][k];l++) e[d[2][k][l]][num]=max(c[i],c[j]);
		}
	for(int i=1;i<=3;i++)
	  for(int j=i+1;j<=4;j++)
	  {
	  	num++;
	  	q[num][++p[num]]=i;
	  	q[num][++p[num]]=j;
	  	d[4][i][++t[4][i]]=num;
	  	d[4][j][++t[4][j]]=num;
	  	for(int l=1;l<=t[3][i];l++)
	  	  for(int r=1;r<=t[3][j];r++)
	  	    if(d[3][i][l]==d[3][j][r])
	  	      for(int k=1;k<=p[d[3][i][l]];k++)
	  	    	if(q[d[3][i][l]][k]!=i&&q[d[3][i][l]][k]!=j)
				  e[d[3][i][l]][num]=c[q[d[3][i][l]][k]];
	  }
	num++;
	for(int i=1;i<=3;i++)
	  for(int j=i+1;j<=4;j++)
	    for(int l=1;l<=t[4][i];l++)
	      for(int r=1;r<=t[4][j];r++)
	        if(d[4][i][l]==d[4][j][r])
	        {
	        	int res=0;
	        	for(int k=1;k<=4;k++) if(k!=i&&k!=j) res=max(res,c[k]);
				e[d[4][i][l]][num]=res;
			}
	return;
}
int main()
{
	for(int i=1;i<=4;i++) scanf("%d",&c[i]);
	sort(c+1,c+4+1);
	for(int i=0;i<=25;i++)
	  for(int j=0;j<=25;j++)
	    if(i!=j) e[i][j]=1e9;
	build();
	for(int k=0;k<=num;k++)
	  for(int i=0;i<=num;i++)
	    for(int j=0;j<=num;j++)
	      if(i!=k&&k!=j&&e[i][k]!=1e9&&e[k][j]!=1e9)
	        e[i][j]=min(e[i][j],e[i][k]+e[k][j]);
	printf("%d\n",e[0][num]);
	return 0;
}

N人过桥+一个手电筒

解析

• 考虑贪心做法；我们把用最快的人作为送回手电筒的人，将最慢和次慢的人运送到对岸所花费的时间和用次快的人作为送回手电筒的人，将最快的人和最慢的人运送到对岸所花费的时间进行比较，每次往答案 ans 里添加较小的时间并将人数减少 2 (n-=2) ，可以证明这样贪心是正确的
• 对于剩余的人数小于 4 (n<4) 的情况：

  n=3 时，加上三人花费时间之和
  n=2 时，加上两人中花费时间较大的那人的花费时间
  n=1 时，加上这个人的花费时间

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
const int N=1e6+5;
int n,ans,c[N];
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&c[i]);
	sort(c+1,c+n+1);
	while(n>=4)
	{
		if(2*c[1]+c[n]+c[n-1]<c[1]+2*c[2]+c[n]) ans+=2*c[1]+c[n]+c[n-1];
		else ans+=c[1]+2*c[2]+c[n];
		n-=2;
	}
	if(n==3) ans+=c[1]+c[2]+c[3];
	else if(n==2) ans+=c[2];
	else if(n==1) ans+=c[1];
	printf("%d\n",ans);
	return 0;
}