【力扣】第224场周赛

1 可以形成最大正方形的矩形数目

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-rectangles-that-can-form-the-largest-square

给你一个数组 rectangles ，其中 rectangles[i] = [$l_i$, $w_i$] 表示第 i 个矩形的长度为$l_i$ 、宽度为$w_i$ 。

如果存在 k 同时满足 $k <= l_i$ 和 $k <= w_i$ ，就可以将第 i 个矩形切成边长为 k 的正方形。例如，矩形 [4,6] 可以切成边长最大为 4 的正方形。

设 maxLen 为可以从矩形数组 rectangles 切分得到的 最大正方形 的边长。

返回可以切出边长为 maxLen 的正方形的矩形 数目 。

示例 1：

输入：rectangles = [[5,8],[3,9],[5,12],[16,5]]
输出：3
解释：能从每个矩形中切出的最大正方形边长分别是 [5,3,5,5] 。
最大正方形的边长为 5 ，可以由 3 个矩形切分得到。
示例 2：

输入：rectangles = [[2,3],[3,7],[4,3],[3,7]]
输出：3

第一题比较简单，主要是字典的灵活使用，

class Solution:
    def countGoodRectangles(self, rectangles: List[List[int]]) -> int:
        a = {}    
        for l,r in rectangles:
            k = min(l,r)
            a.setdefault(k,0)
            a[k] += 1
        return a.get(max(a.keys()))

2 同积元组：

给你一个由 不同 正整数组成的数组 nums ，请你返回满足 a * b = c * d 的元组 (a, b, c, d) 的数量。其中 a、b、c 和 d 都是 nums 中的元素，且 a != b != c != d 。

 来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/tuple-with-same-product

示例 1：

输入：nums = [2,3,4,6]
输出：8
解释：存在 8 个满足题意的元组：
(2,6,3,4) , (2,6,4,3) , (6,2,3,4) , (6,2,4,3)
(3,4,2,6) , (4,3,2,6) , (3,4,6,2) , (4,3,6,2)
示例 2：

输入：nums = [1,2,4,5,10]
输出：16
解释：存在 16 个满足题意的元组：
(1,10,2,5) , (1,10,5,2) , (10,1,2,5) , (10,1,5,2)
(2,5,1,10) , (2,5,10,1) , (5,2,1,10) , (5,2,10,1)
(2,10,4,5) , (2,10,5,4) , (10,2,4,5) , (10,2,4,5)
(4,5,2,10) , (4,5,10,2) , (5,4,2,10) , (5,4,10,2)

步骤：
1.用字典保存两两元素的乘积的频率，key 为乘积，value 为该乘积出现的次数。
如：nums[i] = 1, nums[j] = 12, 则 tmp = {12:1}. nums[i] = 2, nums[j] = 6, 则 tmp = {12:2}.
2.根据乘积出现的频率，计算能够得到这个乘积的元组（长度为4）个数。
如：tmp[12] = 2 说明有 2 个长度为 2 的元组可以得到乘积 12，现在要拼成长度为 4 的元组，共有 (2 * 1) / 2 个组合。
公式为： (n * (n-1)) / 2
3.一个元组可以通过不同的顺序排出 8 个不同的元组，所以结果应该等于 元组个数 * 8。
集合 (a,b,c,d) 可以得到 8 个组合：(a,b,c,d), (a,b,d,c), (b,a,c,d), (b,a,d,c), (c,d,a,b), (c,d,b,a), (d,c,a,b), (d,c,b,a)

作者：datoo
链接：https://leetcode-cn.com/problems/tuple-with-same-product/solution/python-shuang-bai-by-datoo-s8qk/
来源：力扣（LeetCode）

class Solution:
    def tupleSameProduct(self, nums: List[int]) -> int:
        '''
        使用库函数版
        '''
        tmp = collections.defaultdict(int)
        for i in range(len(nums)):
            for j in range(i+1, len(nums)):
                pro = nums[i] * nums[j]
                tmp[pro] += 1
        res = 0
        for val in tmp.values():
            res += (val * (val-1)) // 2
        return res * 8

作者：datoo
链接：https://leetcode-cn.com/problems/tuple-with-same-product/solution/python-shuang-bai-by-datoo-s8qk/
来源：力扣（LeetCode）

class Solution:
    def tupleSameProduct(self, nums: List[int]) -> int:
        '''
        不使用库函数版
        '''
        tmp = dict()
        for i in range(len(nums)):
            for j in range(i+1, len(nums)):
                pro = nums[i] * nums[j]
                if pro not in tmp:      #这两句可用 tmp.setdefault(pro,0)代替
                    tmp[pro] = 0   
                tmp[pro] += 1
        res = 0
        for val in tmp.values():
            res += (val * (val-1)) // 2
        return res * 8

作者：datoo
链接：https://leetcode-cn.com/problems/tuple-with-same-product/solution/python-shuang-bai-by-datoo-s8qk/
来源：力扣（LeetCode）

3 重新排列后的最大子矩阵

给你一个二进制矩阵 matrix ，它的大小为 m x n ，你可以将 matrix 中的 列 按任意顺序重新排列。

请你返回最优方案下将 matrix 重新排列后，全是 1 的子矩阵面积。

 来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-submatrix-with-rearrangements

示例 1：

 

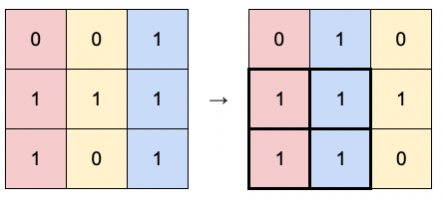
输入：matrix = [[0,0,1],[1,1,1],[1,0,1]]
输出：4
解释：你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分，面积为 4 。
示例 2：

输入：matrix = [[1,0,1,0,1]]
输出：3
解释：你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分，面积为 3 。
示例 3：

输入：matrix = [[1,1,0],[1,0,1]]
输出：2
解释：由于你只能整列整列重新排布，所以没有比面积为 2 更大的全 1 子矩形。
示例 4：

输入：matrix = [[0,0],[0,0]]
输出：0
解释：由于矩阵中没有 1 ，没有任何全 1 的子矩阵，所以面积为 0 。

1.参数定义
m/n：矩阵行和列大小
arr；长度为n的数组，记录该行向上连续1的个数
tmp：为arr逆序排序后的数组
res：返回值，最大矩阵面积
2.思路
依次遍历每行结果，如果当前位置matrix[i][j]为1，则arr[j]+=1，否则arr[j]=0
对arr逆序排序后赋值给tmp，从前往后遍历，以当前值为高的矩阵面积即为arr[j]*(j+1)。例如tmp=[5,4,3,2,1],4对应的下标为1，所以以4为高的矩阵面积即为4*(1+1)=8
res记录每次计算的矩阵最大面积即可
3.复杂度分析
时间复杂度：O(mnlogn)
空间复杂度：O(n)

作者：yim-6
链接：https://leetcode-cn.com/problems/largest-submatrix-with-rearrangements/solution/python3-ni-xu-pai-lie-qiu-zui-da-ju-zhen-cbay/
来源：力扣（LeetCode）

这个tmp数组排序，说明arr中按照1的多少进行排序，点明题目中我们可以随意换列的顺序意思。

class Solution:
    def largestSubmatrix(self, matrix: List[List[int]]) -> int:
        m,n=len(matrix),len(matrix[0])
        res=0
        arr=[0]*(n)
        for i in range(m):
            for j in range(n):
                if matrix[i][j]==1:
                    arr[j]+=1
                else:
                    arr[j]=0
                    
            tmp=sorted(arr,reverse=True)
            for j in range(n):
                res=max(res,tmp[j]*(j+1))
            
        return res

作者：yim-6
链接：https://leetcode-cn.com/problems/largest-submatrix-with-rearrangements/solution/python3-ni-xu-pai-lie-qiu-zui-da-ju-zhen-cbay/
来源：力扣（LeetCode）