[CSP2020]函数调用
1.考虑只有类型1,2的操作的情况:
假设一个数组依次执行:a[1]+1, *3, a[1]+2, a[3]+2, *2
那么 a[1] = a[1]*3*2 + 1*(3*2) + 2*2 , a[3] = a[3]*3*2 + 2*2 , 数组其余元素均乘上3*2=6倍
发现对于乘法操作,在最后给所有数组元素乘上就好了,
而一个加法操作带的系数就等于它后面的所有乘法操作之积
因此可以倒序处理,从后往前记录已进行的所有乘法操作的积是多少,这样就能计算出每次加法操作带的系数是多少
2.考虑类型3的操作:
- 先考虑乘法:
对于图上的每个点(代表着一种操作),维护一个mul,表示执行一次这个操作会给累计的积乘上多少
对于1类操作,它的mul=1;对于2类操作,它的mul就等于它要乘上的值;而对于3类操作,它的mul等于它直接连向的所有点的mul之积
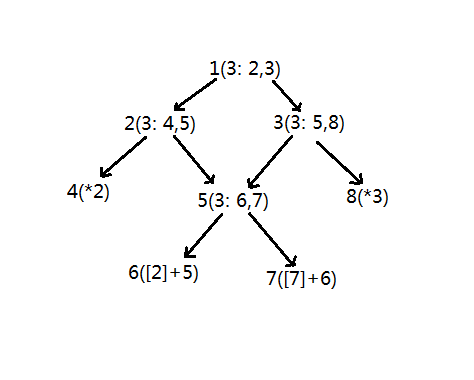
以样例2为例,点2的mul为2,点3的mul为3,所以点1的mul为6,那么执行一次操作1就会让前面执行过的所有的加法操作再乘上6的系数
由题目的条件易得,函数的调用关系构成一个DAG
按照拓扑序倒序扫一遍即可处理出mul
- 再考虑加法:
对于每种类型1或3的操作,维护一个k,表示这个操作带着多少系数
先倒序处理 q 次操作,按照只有类型1,2的方法处理出k,
再把类型3的节点的k下传到它所包含的的类型1的节点,
即可处理出最终的k
- 注意:有些类型3的操作既包含加法又包含乘法
为了确保答案的正确性,必须从后往前倒序处理所有调用的函数
#include<iostream> #include<cstdio> #include<queue> using namespace std; typedef long long ll; const ll mod=998244353; const int N=1000005; struct Edge{ int v,nxt; }edge[N]; ll a[N]; int n,m,Q,F[N],cnt,head[N],d[N],rnd[N],len; queue<int> q; struct func{ int tp,p; ll v,mul,k; }b[N]; void addedge(int u,int v){ edge[++cnt].v=v; edge[cnt].nxt=head[u]; head[u]=cnt; d[v]++; } void tuopu(){ for(int i=1;i<=m;i++) if(!d[i]) q.push(i); while(!q.empty()){ int u=q.front(); q.pop(); rnd[++len]=u; for(int i=head[u];i;i=edge[i].nxt){ int v=edge[i].v; d[v]--; if(!d[v]) q.push(v); } } } void getmul(){ for(int i=m;i>=1;i--){ int u=rnd[i]; for(int j=head[u];j;j=edge[j].nxt){ int v=edge[j].v; b[u].mul=1ll*b[u].mul*b[v].mul%mod; } } } void getk(){ for(int i=1;i<=m;i++){ int u=rnd[i]; ll now=1; for(int j=head[u];j;j=edge[j].nxt){ int v=edge[j].v; b[v].k=(b[v].k+b[u].k*now%mod)%mod; now=now*b[v].mul%mod; } } } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); scanf("%d",&m); for(int i=1;i<=m;i++){ scanf("%d",&b[i].tp); if(b[i].tp==1){ scanf("%d%lld",&b[i].p,&b[i].v); b[i].mul=1; } else if(b[i].tp==2){ scanf("%lld",&b[i].v); b[i].mul=b[i].v; } else{ scanf("%d",&b[i].p);b[i].mul=1; for(int j=1,x;j<=b[i].p;j++){ scanf("%d",&x); addedge(i,x); } } } tuopu(); getmul(); scanf("%d",&Q); for(int i=1;i<=Q;i++) scanf("%d",&F[i]); ll now=1; for(int i=Q;i>=1;i--){ int x=F[i]; b[x].k=(b[x].k+now)%mod; now=now*b[x].mul%mod; } getk(); for(int i=1;i<=n;i++) a[i]=a[i]*now%mod; for(int i=1;i<=m;i++){ if(b[i].tp==1) a[b[i].p]=(a[b[i].p]+b[i].v*b[i].k%mod)%mod; } for(int i=1;i<=n;i++) printf("%lld ",a[i]); return 0; }

