滑块拼图

 

这个图相信大家都不陌生，没错，今天我们要探讨的就是滑块拼图这个游戏的一些性质

这里先放一个滑块拼图的定义：

翻译过来大概是： 一个 n×m 的滑块拼图指的是 把 n×m-1 个滑块放在一个 m 行 n 列的网格里玩的游戏

接下来，我们一起研究一下以下这些问题：

⒈对于一个 n×m 的滑块拼图，一共有多少种排列组合方式？  (n×m)!

理由：把空格也当成一个滑块，一共有 n×m 个互不相同的滑块，共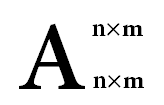种排列方法

⒉所有的组合都是合法的吗？（合法指能够还原到顺序排列状态）不是

理由：举个例子就知道了

　　　　

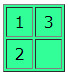
如上图，不管怎么移动，2 和 3的位置都无法互换

3.怎么判断一种组合是否合法？

对于 一个 n×n 的网格，先将表格铺平：

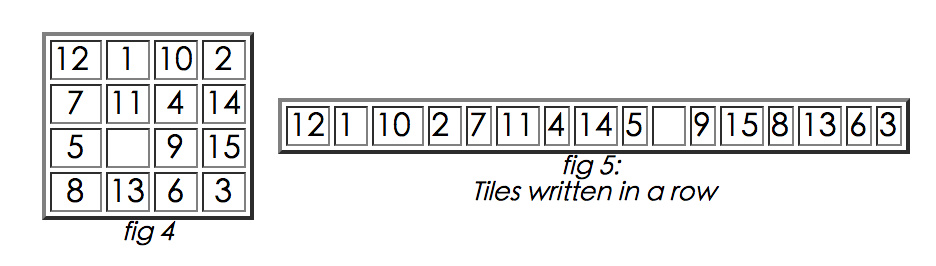
计算 N=逆序数对之和（不算空格），e=空格所在的行数

若n为奇数，当且仅当 N为偶数 时合法

若n为偶数，当且仅当 N+e为偶数 时合法

理由：这个比较复杂，我们分三个命题证明一下

命题1：当 n为奇数时，移动后 N奇偶性不变

首先，某一滑块左右移动，不影响滑块相对顺序，N不变

其次，某一滑块上下移动，N不改变奇偶性，为什么呢？

我们来看张图：

一滑块上下移动一次，在铺平后的序列上相当于跨过了 (n-1) 个数

原本，这 (n-1) 个数每个都和此滑块构成了一个顺序对或逆序对，不妨设其中顺序对有 a 个，逆序对有 b 个 (a+b=n，a>=0，b>=0)

移动后，顺序对变为逆序对，逆序对变为顺序对，即 顺序对有 b 个，逆序对有 a 个

因为 n 为奇数，所以 (n-1) 为偶数

所以 a，b 均为偶数 或 a，b 均为奇数

互换后，这 (n-1) 个数对中逆序对奇偶性不变

又因为此滑块的上下移动不对其它数对造成影响 ，所以 N 奇偶性不变

命题2：当 n为偶数时，移动后 N+e 奇偶性不变

还是，某一滑块左右移动均不对 N，e 造成影响，N+e 不变

然后，我们再来看一下某一滑块上下移动的图：

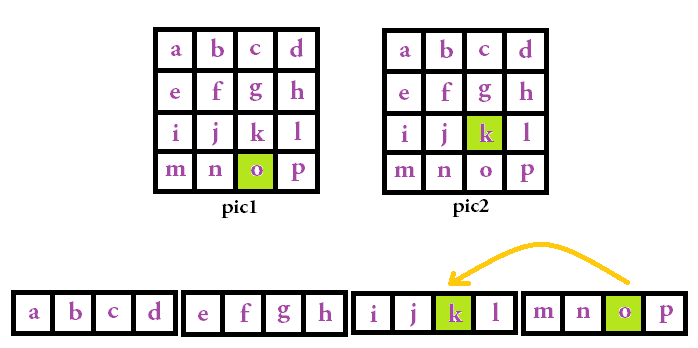
这次，n 为偶数，所以 (n-1) 为奇数

所以 a，b 一奇一偶

互换后，这 (n-1) 个数对中逆序对奇偶性改变

又因为此滑块的上下移动不对其它数对造成影响 ，所以 N 奇偶性改变

但因为此滑块上下移动时，e 的奇偶性也必然改变，所以 N+e 奇偶性不变

命题3：滑块顺序排列时，滑块拼图满足上述判定条件

当 n 为奇数且滑块顺序排列时，N=0，为偶数

当 n 为偶数且滑块顺序排列时，N=0，e=n，N+e=n，为偶数

又因为每步移动均符合命题1和命题2，所以判定成立