余数(数论分块)
题目描述:
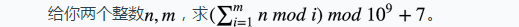
题解:
首先容易想到:当 i > n 时,n mod i = n
所以如果 m > n ,
ans+=((m-n)%mod)*(n%mod)%mod;
m=n;
接下来考虑 i<=n 的情况:
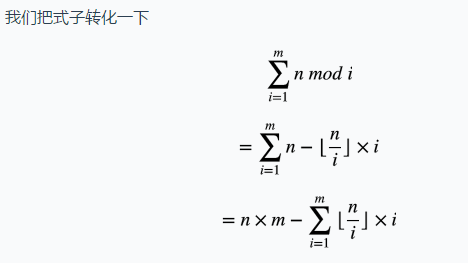
后面这个东西很明显可以用数论分块算,时间复杂度是O(sqrt(N))
但我当时做的时候还没有学数论分块,所以代码十分丑陋
#include<iostream> #include<cstdio> #include<cmath> using namespace std; typedef long long ll; const ll mod=1e9+7; ll n,m,ans; ll l,r,h,t,cnt,sum; int main(){ scanf("%lld%lld",&n,&m); if(n<=m){ ans+=((m-n)%mod)*(n%mod)%mod; ll sq=sqrt(n); for(ll i=1;i<=n/(sq+1);i++) ans=(ans+(n%i))%mod;//这一区间内的n%i没有特殊规律,只能硬算 for(ll i=sq;i>0;i--){//此处i表示除完以后向下取整的结果 l=n/(i+1)+1;r=n/i;//用n除以[l,r]区间内的数取整完结果均为i //统计 n mod 这些数的余数就是求等差数列:n-i*l,n-i*(l+1),...,n-i*r 的和 h=n-l*i,t=n-r*i;//首项,末项 cnt=r-l+1,sum=h+t;//项数,首项加末项的和 if(cnt&1ll)sum>>=1; else cnt>>=1;//除以2 if(l<=r) ans=(ans+(cnt%mod)*(sum%mod))%mod; } } else{ ll sq=sqrt(n);//基本同上 if(m<=(n/(sq+1))){ for(ll i=1;i<=m;i++) ans=(ans+(n%i))%mod; } else{ for(ll i=1;i<=n/(sq+1);i++) ans=(ans+(n%i))%mod; for(ll i=sq;i>0;i--){ l=n/(i+1)+1;r=n/i; if(r>=m) r=m; h=n-l*i,t=n-r*i; cnt=r-l+1,sum=h+t; if(cnt&1ll)sum>>=1; else cnt>>=1; if(l<=r) ans=(ans+(cnt%mod)*(sum%mod))%mod; if(r==m) break; } } } printf("%lld",ans); return 0; }


