[JLOI2013] 赛车（计算几何）

把每一辆赛车看成一条直线：y = v * t + b

其中 v表示速度，t表示时间，b表示初始位置

问题变成：求存在t使得直线的y值在所有直线中最大（允许一样大）

具体做法是

1. 把直线按 v（斜率） 排序
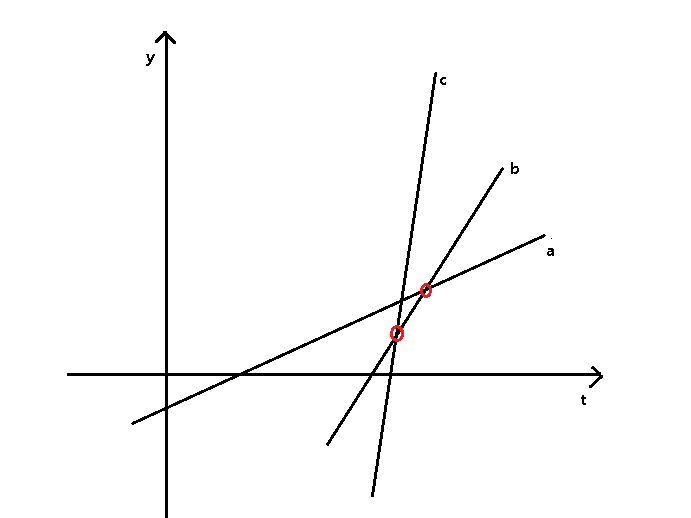
2. 对于有序直线 a, b, c, 如果 b, c 的交点在 a, b 的交点左边，舍去 b

　　　　（如图所示，b 永远无法领头）

　　3.因为 t>=0，所以舍去交点不在第一象限的情况

ps:两直线交点横坐标求法：

y=k1*x+b1　　①

y=k2*x+b2　　②

由 ①，② 得：

k1*x+b1=k2*x+b2

(k1-k2)*x=b2-b1

x=(b2-b1)/(k1-k2)

#include<queue>
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=500010;
int n,sta[maxn],id[maxn],ans[maxn];
struct Car{int b,k,id;}c[maxn];
int top=0,cnt=0;
bool flag[maxn];
bool cmp(const Car &a,const Car &b){
    return a.k<b.k||(a.k==b.k&&a.b>b.b);
}
double getx(int x,int y){
    if (c[y].k-c[x].k==0) return 1e10;
    return (double)((double)c[x].b-c[y].b)/(double)(c[y].k-c[x].k);
}
int main(){
    scanf("%d",&n);
    for (int i=1;i<=n;++i) scanf("%d",&c[i].b);
    for (int i=1;i<=n;++i) scanf("%d",&c[i].k);
    for (int i=1;i<=n;++i) c[i].id=i;
    sort(c+1,c+n+1,cmp);
    sta[++top]=1; id[top]=c[1].id;
    for (int i=2;i<=n;++i){
        if (c[i].k==c[i-1].k&&c[i].b<c[i-1].b) continue;
        while (top>1&&getx(sta[top-1],sta[top])>getx(sta[top],i)) top--;
        sta[++top]=i; id[top]=c[i].id;
    }
    for (int i=2;i<=top;++i)
        if (getx(sta[i-1],sta[i])<0) flag[i-1]=1;
    for (int i=1;i<=top;++i)
        if (!flag[i]) ans[++cnt]=id[i];
    sort(ans+1,ans+cnt+1);
    printf("%d\n",cnt);
    for (int i=1;i<cnt;++i) printf("%d ",ans[i]);
    if (cnt) printf("%d",ans[cnt]);
}