Cool Slogans(后缀自动机+线段树+dp)

传送门：https://www.luogu.org/problemnew/show/CF700

先手动模拟一下：

原串：abracadabra

s数组依次是：abracadabra，abra，a

可以发现，每一步我们找最长的在上一个串中出现两次的子串，即可得到最优解

很容易想到dp：

定义两个数组：
dp[i]:使用节点i最长的那个字符串的答案
mx[i]:节点i最长的那个字符串对应的节点

设A是B的子串
if(A在B中出现两次) dp[B]=dp[A]+1,mx[B]=B;
else dp[B]=dp[A],mx[B]=mx[A];

接下来只需要检查A在B中出现两次就行了：

于是考虑一下维护每一个点的endpos集合，这个只要用线段树就行了。

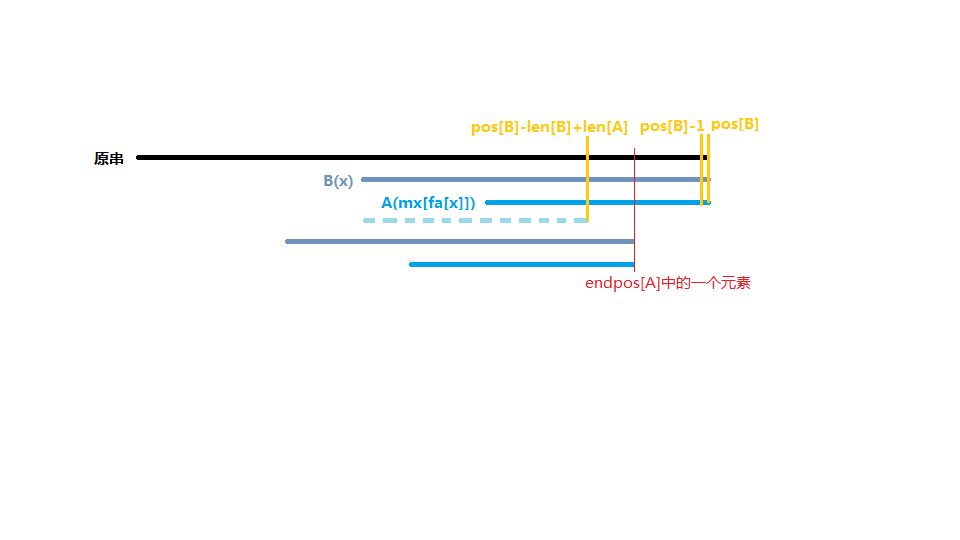
如果A在B中出现了两次，那么A的endpos集合在[pos[B]−len[B]+len[A],pos[B]]中出现了至少两次（其中pos[B]表示B的任意一个endpos）。

所以可以在parent树上dp,由父亲节点转移到儿子节点。

令A=mx[fa[x]],B=x,因为parent树上父亲是儿子的严格后缀，所以必然在儿子里出现了一次，那么只要考虑endpos[A]中是否有元素在[pos[B]−len[B]+len[A],pos[B]−1]中就行了

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=400005;
struct node{
    int ls,rs;
}st[maxn*50];
int sz,rt[maxn],dp[maxn],mx[maxn];
int tot=1,lst=1;
int n,ch[maxn][26],len[maxn],fa[maxn],pos[maxn];
int tax[maxn],id[maxn];
char s[maxn];
void add(int c,int i){
    int p=lst;
    int np=lst=++tot;
    len[np]=len[p]+1;pos[np]=i;
    for(;p&&!ch[p][c];p=fa[p])
        ch[p][c]=np;
    if(!p) fa[np]=1;
    else{
        int q=ch[p][c];
        if(len[q]==len[p]+1) fa[np]=q;
        else{
            int nq=++tot;
            memcpy(ch[nq],ch[q],sizeof ch[q]);
            pos[nq]=i;
            len[nq]=len[p]+1;
            fa[nq]=fa[q];fa[q]=fa[np]=nq;
            for(;p&&ch[p][c]==q;p=fa[p]) ch[p][c]=nq;
        }
    }
}
void insert(int &u,int l,int r,int x){
    if (!u) u=++sz;
    if (l==r) return;
    int mid=(l+r)/2;
    if (x<=mid) insert(st[u].ls,l,mid,x);
    else insert(st[u].rs,mid+1,r,x);
}
int merge(int x,int y){
    if (!x||!y) return x+y;
    int u=++sz;
    st[u].ls=merge(st[x].ls,st[y].ls);
    st[u].rs=merge(st[x].rs,st[y].rs);
    return u;
}
int query(int u,int l,int r,int x,int y){
    if(!u) return 0;
    if(l==x&&r==y) return 1;
    int mid=(l+r)/2;
    if(x<=mid&&query(st[u].ls,l,mid,x,min(y,mid))) return 1;
    if(y>mid&&query(st[u].rs,mid+1,r,max(x,mid+1),y)) return 1;
    return 0;
}
void build(){
    for(int i=1;i<=tot;i++) tax[len[i]]++;
    for(int i=1;i<=tot;i++) tax[i]+=tax[i-1];
    for(int i=1;i<=tot;i++) id[tax[len[i]]--]=i;
    for(int i=tot;i>=2;i--){
        int x=id[i];
        insert(rt[x],1,n,pos[x]);//endpos{x}中插入pos[x] 
        rt[fa[x]]=merge(rt[fa[x]],rt[x]);//endpos{fa[x]}等于其子节点endpos{}的集合 
    }
}
int main(){
    scanf("%d",&n);
    scanf("%s",s+1);
    for(int i=1;i<=n;i++) add(s[i]-'a',i);
    build();
    int ans=1;
    for (int i=2;i<=tot;i++){
        int x=id[i];
        if(fa[x]==1){dp[x]=1;mx[x]=x;continue;} 
        int flag=query(rt[mx[fa[x]]],1,n,pos[x]-len[x]+len[mx[fa[x]]],pos[x]-1);
        if(flag) dp[x]=dp[fa[x]]+1,mx[x]=x;
        else dp[x]=dp[fa[x]],mx[x]=mx[fa[x]];
        ans=max(ans,dp[x]);
    }
    printf("%d",ans);
    return 0;
}