USACO 2020 OPEN Silver Problem 3. The Moo Particle
题意:

解法:
首先给出在本题中连通和连通块的定义:
连通:
两个粒子a,b连通,当且仅当ax≤bx、ay≤by或者bx≤ax、by≤ay。

如图,A,B两粒子是连通的,而C、D不是。
可以看出,本题中连通的定义类似于无向边。
连通块:
一个有n个粒子的粒子集合S被称为连通块,当且仅当该集合内的粒子可以通过相互作用仅留下任意一个粒子。

左侧的A图中的四粒子属于同一连通块,而右侧的B图中四粒子分别属于两个连通块。
50分暴力:
显然,最少留下的粒子(以下简称为点)数等于连通块的总数,故本题可以转化为求最小的连通块划分数。通过该结论可以写出50分暴力(n≤1000)。
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; int n, ans, fa[N], dx[N], dy[N]; bool cont (int x, int y) { if (dx[x] <= dx[y] && dy[x] <= dy[y]) return true; if (dx[x] >= dx[y] && dy[x] >= dy[y]) return true; return false; } int find (int x) { if (x != fa[x]) return fa[x] = find (fa[x]); return x; } void merges (int x, int y) { int xx = find (x), yy = find (y); if (xx == yy) return ; fa[xx] = yy; return ; } int main () { freopen ("moop.in", "r", stdin); freopen ("moop.out", "w", stdout); scanf ("%d", &n); for (int i = 1; i <= n; i ++) { scanf ("%d %d", &dx[i], &dy[i]); fa[i] = i; } for (int i = 1; i <= n; i ++) for (int j = i + 1; j <= n; j ++) if (cont (i, j)) merges (i, j); for (int i = 1; i <= n; i ++) if (fa[i] == i) ans ++; printf ("%d\n", ans); return 0; }
满分解法:
O(n2)暴力连边判断连通块的方法显然是不行的。所以需要找到一种快速划分连通块的方法。
考虑按每个点的x坐标排序并记录排序完成后的y坐标并用数组(a)记录,则可以快速离散化所有点的坐标。(当两点x相同时两点必定连通,故不需要特别讨论x坐标相同的情况)
考虑一个在x轴上连续的点集,满足该点集最左侧的点的y坐标比最右侧的点的y坐标小。(如图)

L、R分别为该点集中最左侧、最右侧的点。
显然,L与R连通。
将点集中剩下的点分为三类:
A类:在R点左上方(如A点)
B类:在R点左下方并且在L点右上方(如B点)
C类:在L点右下方(如C点)
对每类点的连通情况进行讨论:
A类:
因为A点在R点左上方,故A点y坐标比L大、x坐标比L大。所以该点与L点连通。
B类:
因为B点在L点右上方和R点左下方,故与L、R点都连通。
C类:
因为C点在L点右下方,故C点y坐标比R小,x坐标比R小,所以该店与R点连通。
综上所述,A、B、C类点都与L、R中的一点连通,而L又与R点连通。
可得到结论:任意一个满足最左侧的点的y坐标比最右侧的点的y坐标小的在x轴上连续的点集都满足连通块的定义。
由此可以得到一种O(n)的贪心的连通块划分方法:从左往右扫描所有点,若当前点的y值小于上一个点所属的连通块的L点的y值,则从该点开始新建一个连通块,并记录该点的y坐标。
但此贪心方法有明显错误,如图:
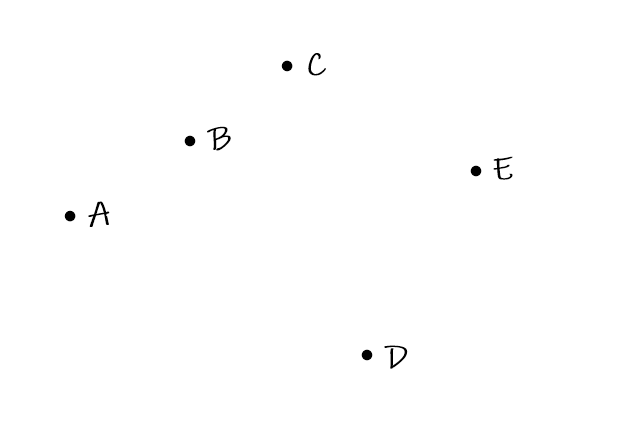
按照这种贪心方法,该点集会被划分为(A、B、C)和(D、E)两个连通块。实际上(A、B、C、D、E)即为一个连通块。
此时可以发现,若记录划分到当前点前每个连通块的L点的y坐标,并在每个点用二分算法判断该点y坐标最大大于哪个L点(设为l点)y坐标并将l点之后的所有点与l点合并为一个连通块,就可以在logn时间内更加准确地判断出到目前点为止最小的连通块划分数。
但这种判断方法仍然有问题,如图:
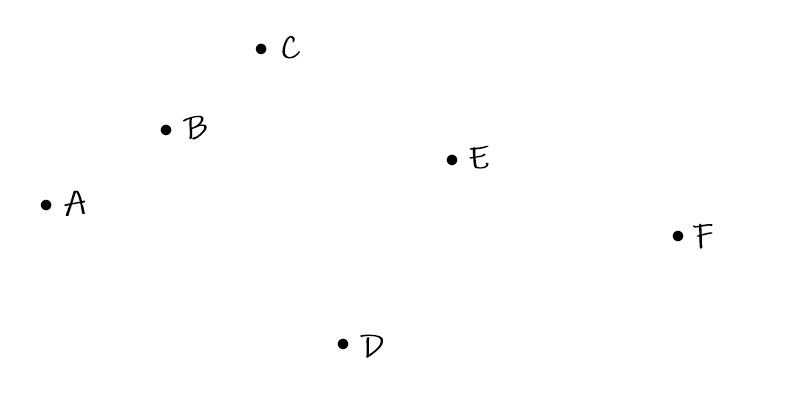
点(A、B、C、D、E、F)为一个连通块,但按照当前贪心方法会划分出(A、B、C、D、E)和(F)两连通块。故我们需要进一步优化贪心方法。
在原贪心方法中,我们记录的是到目前点为止,划分出的所有连通块的L节点的y值,但并入一个连通块并不一定需要大于该连通块的L点,仅需要在该联通块最右侧的点的右侧并大于该连通块的最小点即可。
故在合并连通块的时候,可以把原连通块的L节点的y值更新为现连通块L节点的y值。
这样即可求出最小连通块划分数。
代码如下:
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; int n, a[N], cnt, mn[N]; pair <int, int> p[N]; int main () { freopen ("moop.in", "r", stdin); freopen ("moop.out", "w", stdout); scanf ("%d", &n); for (int i = 1; i <= n; i ++) scanf ("%d %d", &p[i].first, &p[i].second); sort (p + 1, p + n + 1); for (int i = 1; i <= n; i ++) a[i] = p[i].second; for (int i = 1; i <= n; i ++) { if (i == 1 || -mn[cnt] > a[i]) { cnt ++; mn[cnt] = -a[i]; continue ; } if (cnt == 1) continue; if (-mn[cnt - 1] <= a[i]) { int mnn = mn[cnt]; int ls = lower_bound (mn + 1, mn + cnt + 1, -a[i]) - mn; cnt = ls; mn[cnt] = mnn; } } printf ("%d\n", cnt); return 0; }


