反馈习题
准备秋招笔试的过程中发现,无论看书浏览多少遍,真到做题的时候还是空白。觉得对于这类基础内容还是需要多做题才行,毕竟习题也是从很多实际问题中抽象出来的。或许这也能很好证明理论与实践在学习生涯中的互相关系了吧 =。=!
加油加油吧!
习题8.1
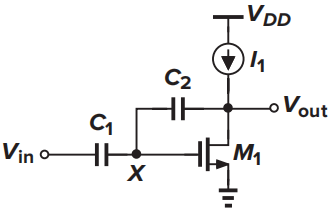
假定\(I_1\)是理想电流源,\(g_{m1}r_{o1}\leq50\),如果要求增益误差\(e_A<5\%\),从这个结构能获得的最大闭环增益为?此时的低频闭环输出阻抗为?
不考虑加载效应时,令开环增益\(g_{m1}r_{o1}=A_0\),理想情况下闭环增益为\(A_{Ideal}=1/\beta\)。由闭环增益的计算公式得到的真实的闭环增益为
\[A_{Real}={V_{out}\over{V_{in}}}={A_0\over{1+\beta A_0}}={A_0/\beta\over{1/\beta+A_0}}={A_{Ideal}A_0\over{A_{Ideal}+A_0}}={1\over{{1\over{A_{Ideal}}}+{1\over{A_0}}}}\tag{1.1}
\]
增益误差可以表示为:
\[e_A={A_{Ideal}-A_{Real}\over{A_{Ideal}}}=1-{1\over{1+{A_{Ideal}\over{A_0}}}}<5\%\tag{1.2}
\]
可以计算出最大闭环增益
\[A_{Ideal}<{A_0\times{5\%\over{95\%}}}<2.632\tag{1.3}
\]
由于是电压-电压反馈,则此时的输出阻抗为
\[Z_{close,out}={Z_{open,out}\over{1+{A_0\over{A_{Ideal,max}}}}}={r_O\over{132.6}}\tag{1.4}
\]
习题8.5
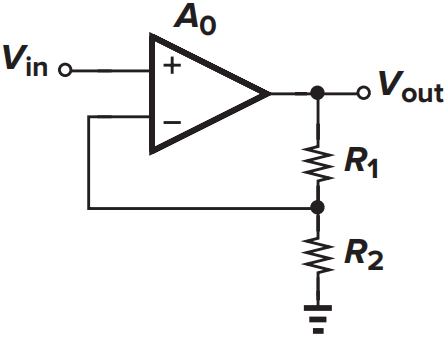
放大器\(A_0\)的输出阻抗为\(R_0\),考虑加载效应后,计算闭环增益和输出阻抗。
首先判断反馈类型,该反馈为电压-电压负反馈,输出电压被分压器\(R_1\)、\(R_2\)分压,再将该电压反馈到运放反相输入端,并且容易证明是负反馈。
电压-电压负反馈的加载效应的开环等效方式为
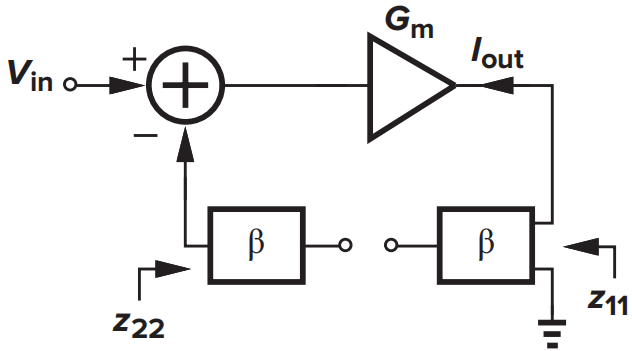
得到的电路图如下,其中计算开环增益时\(V_t\)端开路,计算环路增益时需要从\(V_t\)注入电压信号,测量\(V_f\)的值。
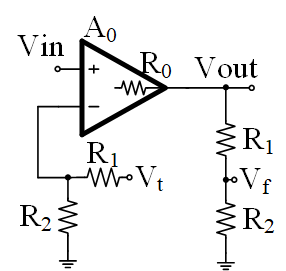
使用此方法开环后的开环增益和开环输出阻抗为:
\[A_{open}={V_{out}\over{V_{in}}}={A_0{R_1+R_2\over{R_0+R_1+R_2}}}\tag{5.1}
\]
\[Z_{out,open}=R_0||(R_1+R_2)\tag{5.2}
\]
环路增益为:
\[LP={V_t\over{V_f}}={{R_2\over{R_1+R_2}}A_0{R_2\over{R_0+R_1+R_2}}}\tag{5.3}
\]
则闭环增益和闭环输出阻抗为:
\[A_{close}={A_{open}\over{1+LP}}={A_0{R_1+R_2\over{R_0+R_1+R_2}}\over{1+{R_2\over{R_1+R_2}}A_0{R_2\over{R_0+R_1+R_2}}}}\tag{5.4}
\]
\[Z_{out,close}={Z_{out,open}\over{1+LP}}={R_0||(R_1+R_2)\over{{R_2\over{R_1+R_2}}A_0{R_2\over{R_0+R_1+R_2}}}}\tag{5.5}
\]
习题8.10
(a)其他题目计算方法类似,不再给出
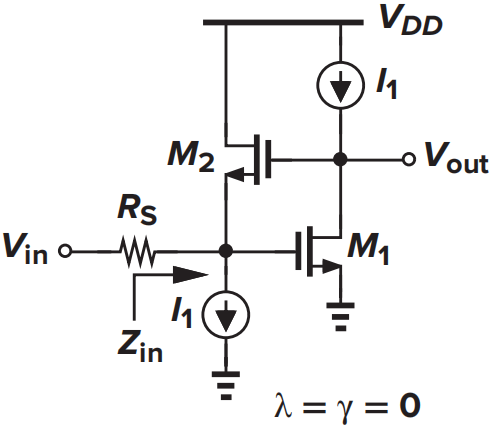
计算输入输出阻抗及电压增益
该反馈为电压-电流反馈。在\(M_2\)的栅极断开环路,此时没有加载效应。令输入信号为0,在\(M_2\)的栅极注入电压信号,并检测\(V_{out}\)端口的电压,得到的环路增益为:
\[LP={R_S\over{R_S+{1\over{g_{m2}}}}}\:g_{m1}r_{O1}\tag{10.a.1}
\]
同样在\(M_2\)的栅极断开环路,保持输入信号\(V_{in}\),检测\(V_{out}\)端口的电压可得开环增益\(A_{open}\),同时在相应端口可以求得开环输入阻抗\(Z_{in,open}\)和开环输出阻抗\(Z_{out,open}\),注意计算输入阻抗时\(R_S\)为电源内阻,不计算。
\[A_{open}={1/g_{m2}\over{R_S+1/g_{m2}}}\:g_{m1}r_{O1}\tag{10.a.2}
\]
\[Z_{in,open}=1/g_{m2}\tag{10.a.3}
\]
\[Z_{out,open}=r_{O1}\tag{10.a.4}
\]
闭环增益为:
\[A_{close}={A_{open}\over{1+LP}}={1/g_{m2}\over{{R_S+1/g_{m2}\over{g_{m1}r_{o1}}}+R_S}}\tag{10.a.5}
\]
\[Z_{in,close}={Z_{in,open}\over{1+LP}}={R_S/g_{m2}+(1/g_{m2})^2\over{g_{m1}r_{o1}R_S}}\tag{10.a.6}
\]
\[Z_{out,close}={Z_{out,open}\over{1+LP}}={R_S+1/g_{m2}\over{g_{m1}R_S}}={1\over{g_{m1}}}+{1\over{g_{m1}g_{m2}R_S}}\tag{10.a.7}
\]
习题8.11
(b)
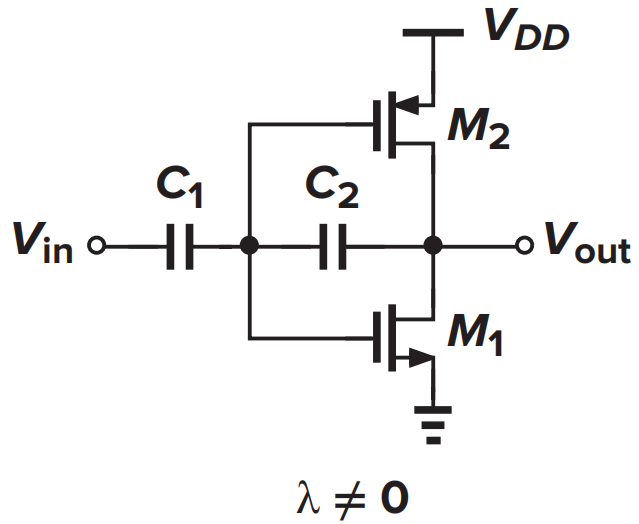
计算输入输出阻抗
解:该反馈为电压-电压反馈,画出小信号模型可以快速地求出输入/输出阻抗
\[Z_{in}={1\over{SC_1}}+{{1\over{SC_2}}+(r_{o1}||r_{o2})\over{1+(g_{m1}+g_{m2})(r_{o1}||r_{o2})}}\tag{11.b.1}
\]
\[Z_{out}={(r_{o1}||r_{o2})\over{1+{C_2\over{C_1+C_2}}[(g_{m1}+g_{m2})(r_{o1}||r_{o2})+sC_1(r_{o1}||r_{o2})]}}\tag{11.b.2}
\]
习题8.15
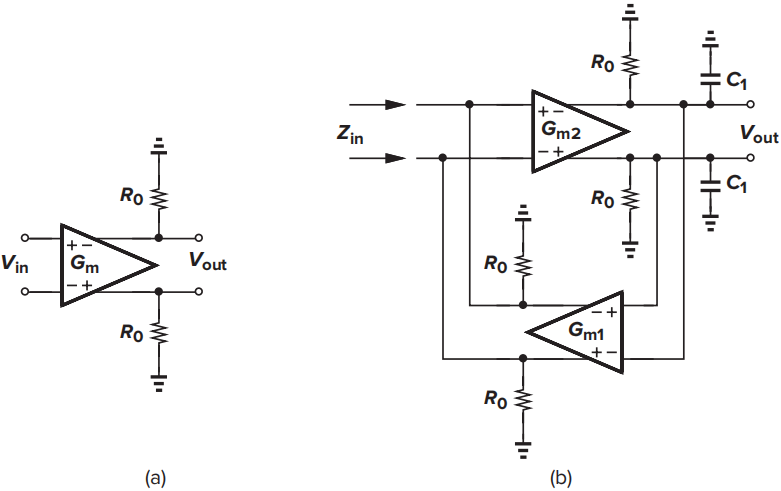
带有电流源负载的差动对可表示如图(a),其中\(R_0=r_{ON}||r_{OP}\),\(r_{ON}\)和\(r_{OP}\)分别表示NMOS和PMOS器件的输出电阻。图(b)把\(G_{m1}\)和\(G_{m2}\)都接在了负反馈环路中。
1)忽略其他电容,求出\(Z_{in}\)的表达式。画出\(|Z_{in}|\)随频率变化的曲线草图。
2)从直观解释1)的结果。
3)根据每个\(G_m\)级的输入参考噪声电压,计算总输入参考噪声电压和电流。
解:1)可以将双端口网络等效为方便计算的单端口网络,注意电流参考方向的变化。
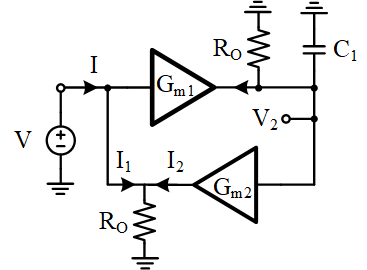
则有
\[I=I_1+I_2={V\over{R_O}}-{[-VG_{m1}(R_O||{1\over{sC_1}})G_{m2}]}\tag{15.1.1}
\]
\[R_{in,close}={R_O(R_OC_1s)\over{R_OC_1s+1+R_O^2G_{m1}G_{m2}}}\tag{15.1.2}
\]
求得零点\(Zero=1/R_OC_1\),极点\(Pole={(1+G_{m1}G_{m2}R_O^2)/R_OC_1}\)。直流时带入\(s=0\)求得\(R_{in,DC}={R_O/(1+R_O^2G_{m1}G_{m2})}\);频率很高时带入\(s=\infty\)求得\(R_{in,AC}=R_O\)。则曲线图
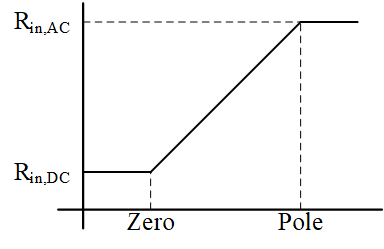
2)低频时,反馈程度较深;频率逐渐升高时,前馈网络输出阻抗下降,使得反馈网络输入电压下降,从而逐渐弱化了反馈的作用。
3)首先求等效输入噪声电压,将输入短路,可以得到\(\overline{V_{out}^2}=4kT\times 2[{2\over{3}}G_{m1}+{1\over R_O}(R_O||{1\over C_1s})]\),将该输出噪声电压除以电压增益的平方,则可求得等效输入噪声电压
\[\overline{V_{n,in}^2}=8kT({2\over 3G_{m1}}+{1\over G_{m1}^2R_O})\tag{15.3.1}
\]
然后求噪声电流,此时需要将输入端开路,可以求得输出此时的输出噪声电压为
\[V_{n,out}=-G_{m1}(R_O||{1\over C_1s})[(V_{n,out}+V_{n2})G_{m2}R_O+V_{n1}]=-{G_{m1}(R_O||{1\over C_1s})(G_{m2}R_OV_{n2})\over{1+G_{m1}(R_O||{1\over C_1s})}G_{m2}R_O}\tag{15.3.2}
\]
其中,\(V_{n1}\)和\(V_{n2}\)是两个\(G_m\)级的等效输入噪声。还需要计算从输入电流到输出电压的跨阻。有
\[-V_{out}=(V_{out}G_{m2}+I_{in})R_OG_{m2}(R_O||{1\over C_1s})\tag{15.3.3}
\]
\[R_m={V_{out}\over{I_{in}}}=-{G_{m1}R_O(R_O||{1\over C_1s})\over{1+G_{m2}G_{m1}R_O(R_O||{1\over C_1s})}}\tag{15.3.3}
\]
则等效输入噪声电流为
\[I_{n,in}={V_{n,out}\over{R_m}}={G_{m2}R_OV_{n2}+V_{n1}\over{R_O}}\tag{15.3.4}
\]
\[\overline{I_{n,in}^2}={G_{m2}^2V_{n2}^2}+{V_{n1}^2\over{R_O^2}}\tag{15.3.5}
\]
习题8.19
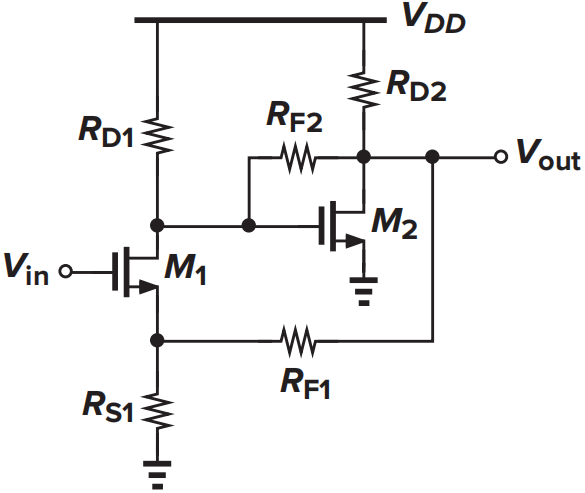
假设所有电阻为2kΩ,\(g_{m1}=g_{m2}=1/(200\Omega)\),假定\(\lambda=\gamma=0\),计算闭环增益和输出阻抗。
解:可以看出该电路中含有两个环路,我们需要对环路做迭代计算。首先拆开最外面的环路,因为需要考虑反馈网络的加载效应。
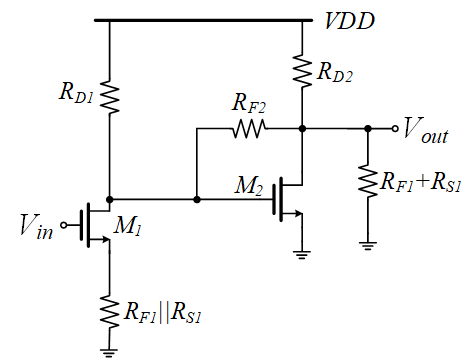
计算由\(M_2\)和\(R_{F2}\)组成的小环路的闭环增益、输入/输出电阻,然后使用电压放大器模型来等效该部分。
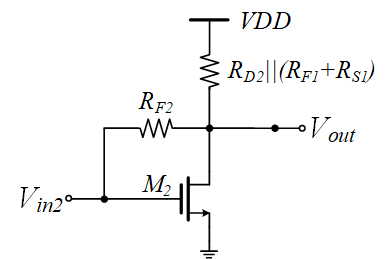
直接使用小信号计算得到
\[R_{in,2}={R_{F2}\over{1+g_{m2}[R_{D2}||(R_{F1}+R_{S1})]}}=261\Omega\tag{19.1}
\]
\[R_{out,2}={R_{D2}||(R_{F2}+R_{S1})\over{1+g_{m2}[R_{D2}||(R_{F1}+R_{S1})]}}=174\Omega\tag{19.2}
\]
\[A_{V2}=({1\over R_{F2}}-g_m)(R_{D2}||R_{F2})=-3.6\tag{19.3}
\]
则回到第一张图可以计算出系统的开环增益和开环输出阻抗
\[A_{open}=-{R_{D1}||R_{in2}\over{R_{F1}||R_{F1}}+{1\over g_{m1}}}\cdot A_{V2}=0.69\tag{19.4}
\]
\[R_{out,open}=R_{out,2}=174\Omega\tag{19.5}
\]
然后在断开环路的结点插入电压源\(V_t\),测试结点另一端\(V_f\),即可得到环路增益\(LP\)
\[V_f=V_t{R_{F1}\over{R_{F1}+R_{S1}}}\cdot{R_{D1}\over{(R_{s1}+R_{F1})+{1\over g_{m1}}}}\cdot{A_{V2}}\cdot{R_{S1}\over{R_{S1}+R_{F1}}}\tag{19.6}
\]
\[LP={V_f\over V_t}=0.75\tag{19.7}
\]
则可以算出系统的闭环增益和输出阻抗了
\[A_{close}={A_{open}\over 1+LP}={0.69\over{1+0.75}}=0.394\tag{19.8}
\]
\[R_{out,close}={R_{out,open}\over{1+LP}}={174\over{1+0.75}}=99.5\Omega\tag{19.9}
\]














 浙公网安备 33010602011771号
浙公网安备 33010602011771号