负反馈 —— 拉扎维 第二版第八章笔记

反馈简介

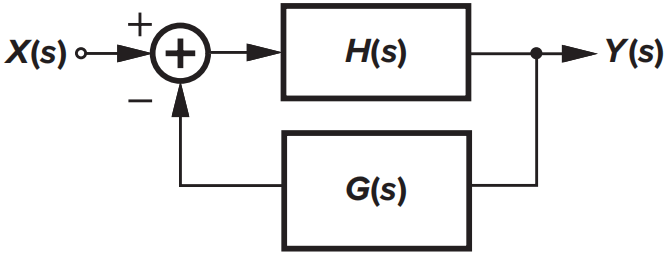
image-20200814135119080

上图是反馈系统的一般表示方式。其中\(H(s)\)叫做前馈网络，\(G(s)\)叫做反馈网络。\(H(s)\)的输入信号为\(X(s)-G(s)Y(s)\)叫做反馈误差。一个设计良好的反馈系统中，反馈误差应该应该接近于零，从而使输出\(Y(s)\)为输入\(X(s)\)的精确比例复制。

由于反馈误差接近于零，因此在前馈网络\(H(s)\)的输入端可以认为是虚地

\(Y(s)/X(s)\)叫做闭环传递函数，\(H(s)\)叫做开环传递函数。因此该系统的闭环传递函数可以写作：

\[{{Y(s)} \over {X(s)}}={{H(s) \over {1+G(s)H(s)}}} \tag{8.1} \]

图片中可以认识到反馈系统的四个部分：

  1. 前馈放大器；
  2. 检测输出的方式；
  3. 反馈网络；
  4. 产生反馈误差的方式，既减（加）法器。
例子 描述
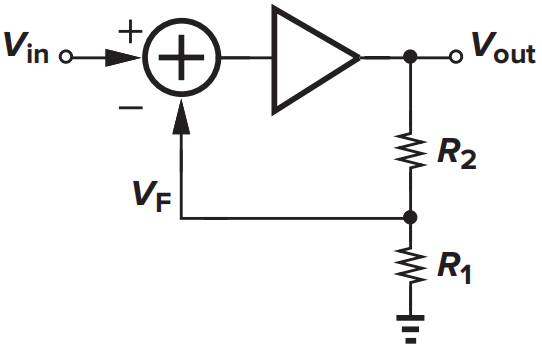image-20200814135204706 输出端又两电阻分压，再反馈回输入，属于电压反馈
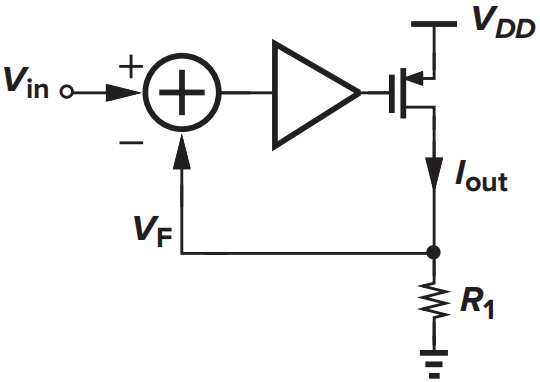image-20200814135239426 输出信号为电流，通过检测串联小电阻\(R_1\)的压降来检测电流，并反馈会输入，属于电流反馈
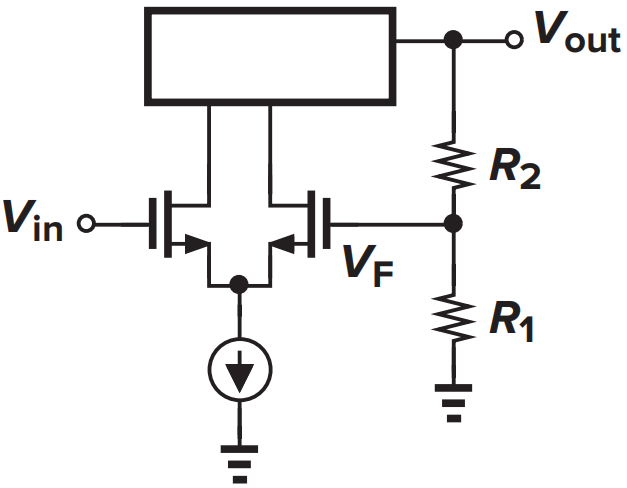image-20200814141710617 输出端通过分压形成反馈电压，属于电压反馈；差分对可以对电压做差，来产生反馈误差。
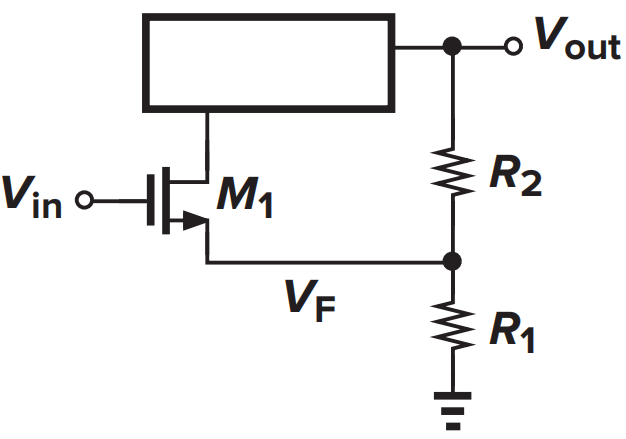image-20200814141742645 输出端通过分压形成反馈电压，属于电压反馈；反馈的电压\(V_F\)接在输入管源极，由于电流\(I_D\)是\(V_{in}-V_F\)的函数，因此是通过对电压做差来产生反馈误差。
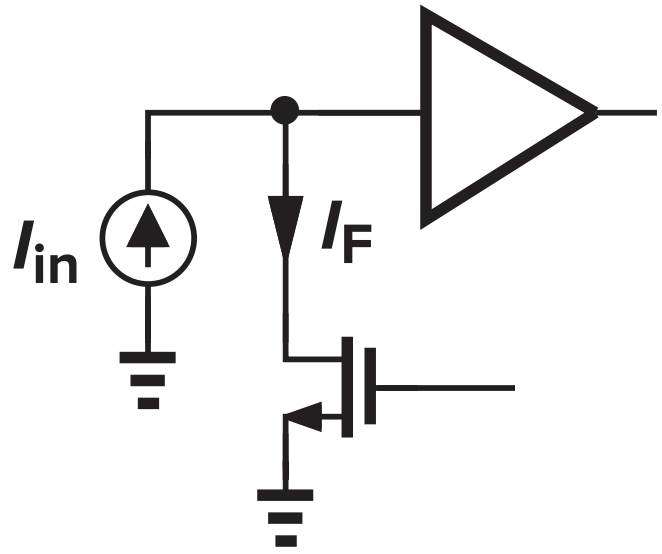image-20200814141757002 反馈到输入的信号与输入端口处于同一节点时，可以实现电流减法。

反馈信号与输入信号的关系：电压相减形式获得反馈误差时，输入信号和反馈信号应处于两个不同节点；电流相减形式获得反馈误差时，输入信号和反馈信号应处于同一节点。

反馈的优势

  1. 降低开环系统的增益灵敏度。开环系统的增益会被很多因素影响，例如工艺、温度、偏置、电源等；但使用负反馈会大大降低其他因素对增益的影响，从而提供一个稳定增益；
  2. 终端阻抗变化。负反馈可以改变输入/输出端口的阻抗，可将相应端口阻抗变化为原来的\(1/(LP+1)\)倍或\((1+LP)\)倍，其中\(LP\)为系统环路增益。
  3. 带宽变化。3dB带宽可以增加\((1+LP)\)倍，但增益带宽积不变，由于增益减小了\((1+LP)\)倍。
  4. 降低非线性。

反馈结构

电压-电压反馈

  • 闭环增益：
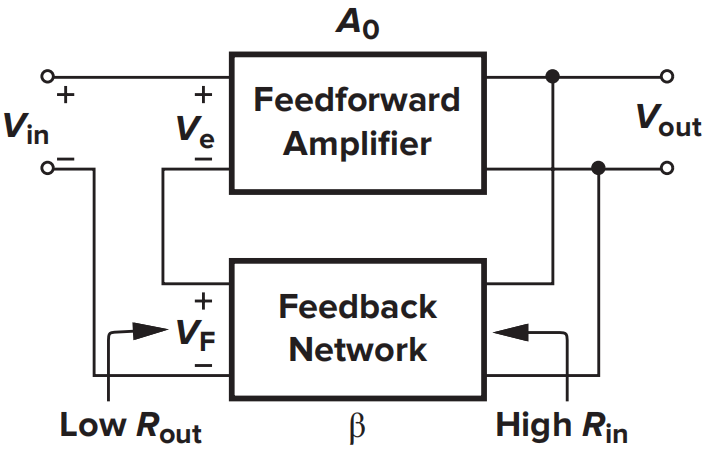
image-20200814141841868

由图中可以得到\(V_F=\beta V_{out}\)，\(V_e=V_{in}-V_F\)，\(V_{out}=A_0V_e\)，因此

\[{V_{out} \over V_{in}}={A_0 \over {1+\beta A_0} }={A_0\over 1+LP}\tag{8.2} \]

其中，环路增益\(LP\)为\(\beta A_0\)，可以看出总的增益减小到原来的\((1+LP)^{-1}\)倍。

  • 输出电阻：
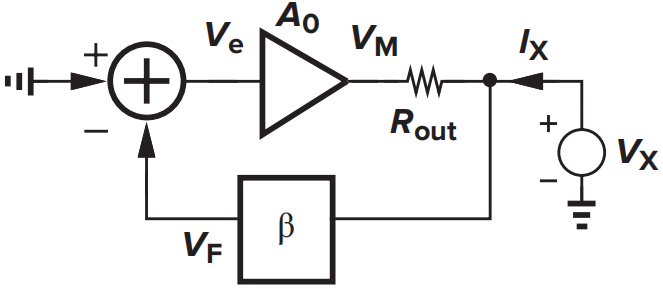
image-20200814142311019

上图为计算输出电阻的等效图，输入信号被置零。\(R_{out}\)代表前馈放大器的输出阻抗。由图可得\(V_F=\beta V_X\)，\(V_e=-\beta V_X\)，\(V_M=-\beta A_0V_X\)，并且电流可以表示为\(I_X=[V_X-(-\beta A_0V_X)]/R_{out}\)，则有

\[{{V_X} \over {I_X}}={R_{out} \over {1+\beta A_0}}={R_{out}\over 1+LP} \tag{8.3} \]

可以看出输出电阻减小为原来的\((1+LP)^{-1}\)倍，使系统接近于理想电压源。

  • 输入电阻：
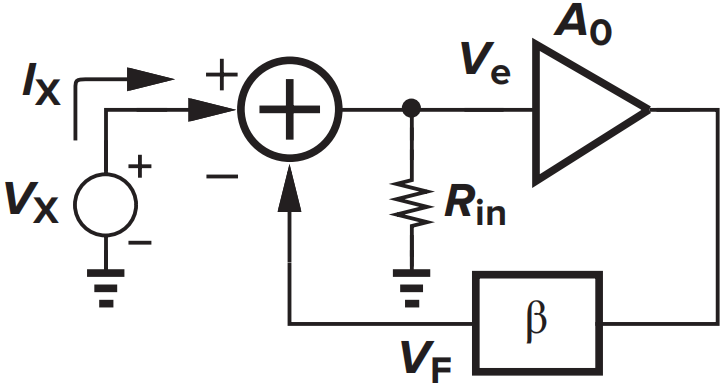
image-20200814142352419

上图为计算输入电阻的等效图。\(R_{in}\)代表前馈放大器的输入阻抗。由图得\(V_e=I_XR_{in}=V_X-V_F\)，\(V_F=\beta A_0V_e\)，则有

\[{{V_X}\over{I_X}}=R_{in}(1+\beta A_0)=R_{in}(1+LP) \tag{8.4} \]

可以看出输入电阻增加为原来的\((1+LP)\)倍，使电路接近于理想电压放大器。

电流-电压反馈

  • 闭环增益：
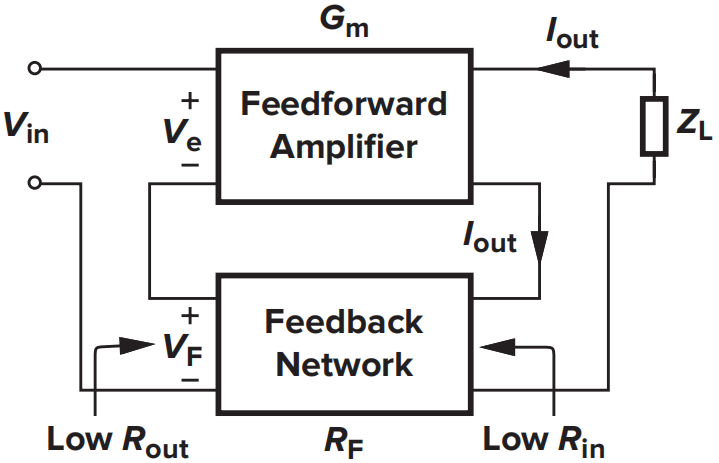
image-20200814142437478

闭环增益为

\[{I_{out}\over {V_{in}}}={G_m\over 1+G_mR_F}={G_m\over 1+LP} \tag{8.5} \]

闭环增益表现为跨导，跨导减小为原来的\((1+LP)^{-1}\)倍。

  • 输出电阻：
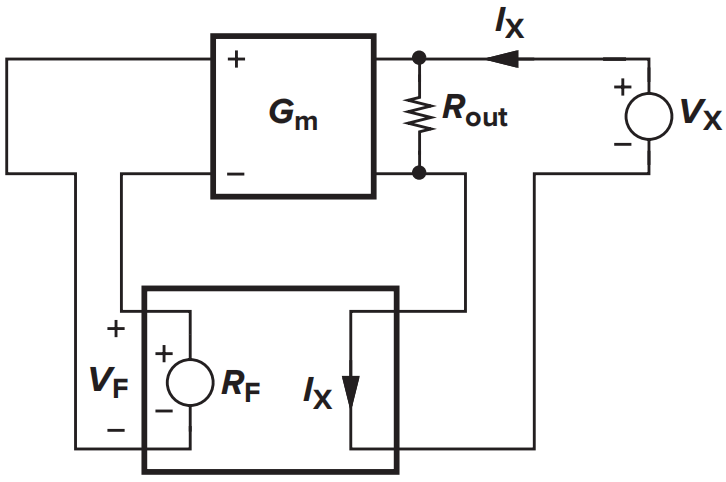
image-20200814142541779

输出电阻为

\[{V_X\over I_X}=R_{out}(1+G_mR_F)=R_{out}(1+LP)\tag{8.6} \]

输出电阻增大为原来的\((1+LP)\)倍。

  • 输入电阻：
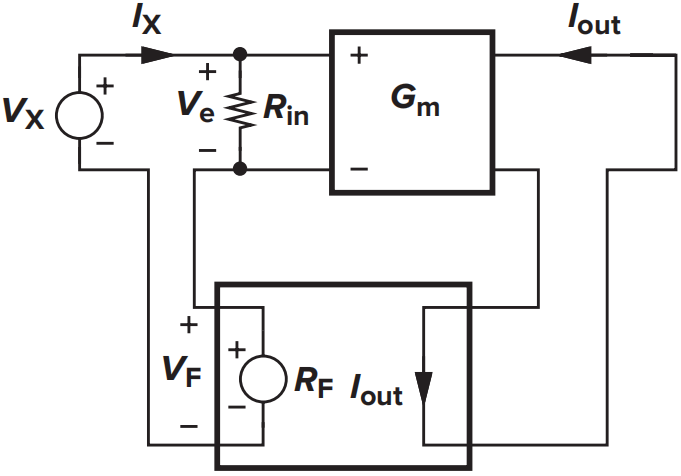
image-20200814142609790

输入电阻为

\[{V_X\over I_X}=R_{in}(1+G_mR_F)=R_{in}(1+LP)\tag{8.7} \]

输入电阻增加为原来的\((1+LP)\)倍

电压-电流反馈

  • 闭环增益：
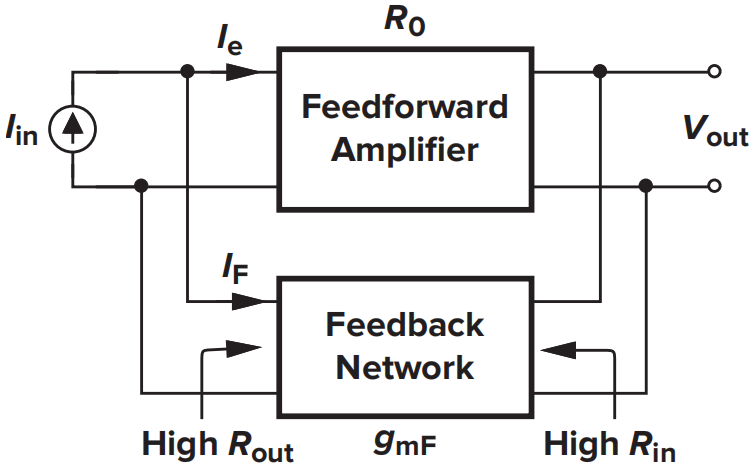
image-20200814142954130

闭环增益为

\[{V_{out}\over I_{in}}={R_0\over{1+g_{mF}R_0}}={R_0\over 1+LP}\tag{8.8} \]

闭环增益表现为阻抗，阻抗减小为原来的\((1+LP)^{-1}\)倍。

  • 输出电阻：
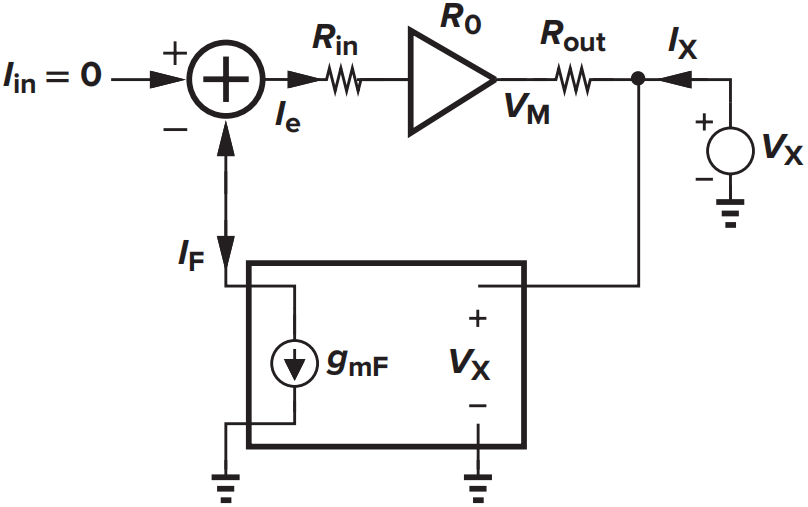
image-20200814143038113

输出电阻为

\[{V_X\over I_X}={R_{out}\over{1+g_{mF}R_0}}={R_{out}\over{1+LP}}\tag{8.9} \]

输出电阻减小为原来的\((1+LP)^{-1}\)倍。

  • 输入电阻：
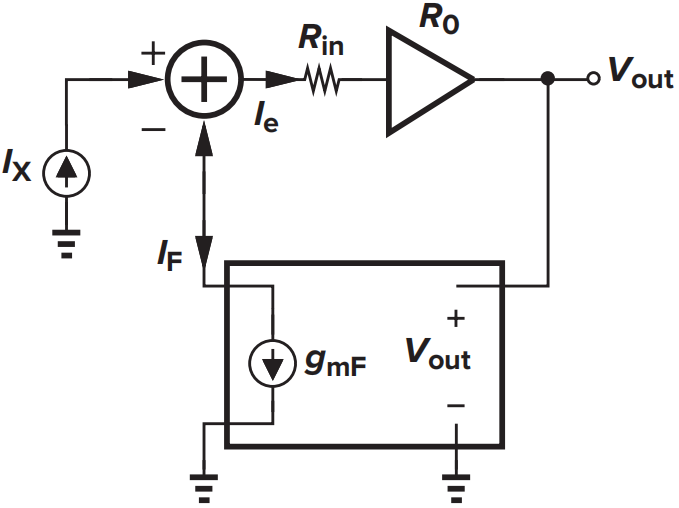
image-20200814143111960

输入电阻为

\[{V_X\over{I_X}}={R_{in}\over{1+g_{mF}R_0}}={R_{in}\over{1+LP}}\tag{8.10} \]

输入电阻减小为原来的\((1+LP)^{-1}\)倍。

电流-电流反馈

  • 闭环增益：
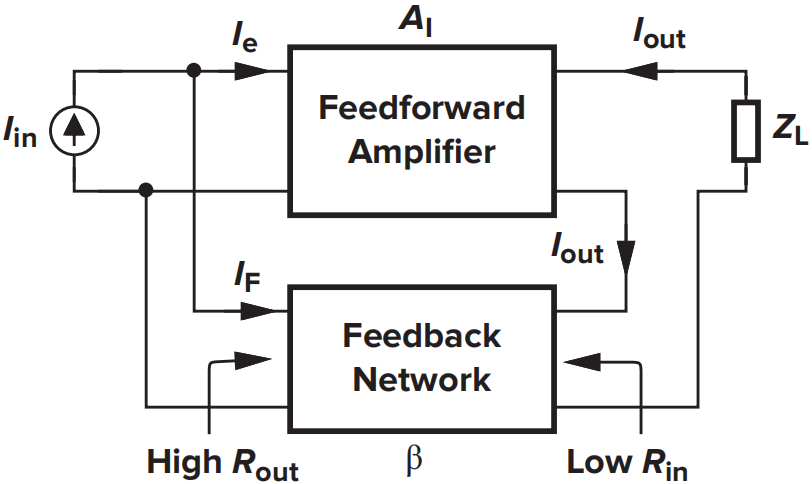
image-20200814143143662

闭环增益为

\[{I_{out}\over{I_{in}}}={A_I\over{1+\beta A_I}}={A_I\over{1+LP}}\tag{8.11} \]

  • 输出电阻：

输出电阻增加为原来的\((1+LP)\)倍

  • 输入电阻：

输入电阻减小为原来的\((1+LP)^{-1}\)倍。

反馈对噪声的影响

在四种反馈类型中，如果反馈网络不引入噪声，则输入参考噪声电压和电流均保持不变。实际上，反馈网络本身包含有电阻和MOS管，会使总的噪声性能变差。

加载效应

实际上反馈网络的非理想效应会使得前馈网络的传递函数发生变化，从而改变最终的闭环增益。因此我们需要将加载效应的影响等效进电路之中。

电压-电压反馈

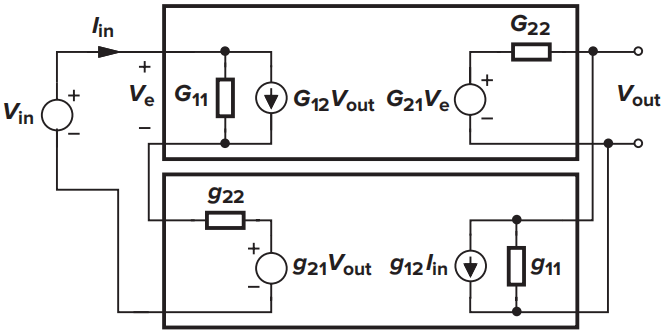
image-20200814143226545

电压-电压反馈使用G模型来表示，其中\(G_{11}\)表示前馈网络输入导纳\((Z_{in})^{-1}\)，\(G_{22}\)表示前馈网络输出阻抗\(Z_{out}\)，\(G_{21}\)表示前馈网络的电压增益\(A_0\)，\(G_{12}\)表示前馈网络的内部反馈；\(g_{11}\)表示反馈网络的输入导纳，\(g_{22}\)表示反馈网络的输出阻抗，\(g_{21}\)表示反馈网络的反馈系数\(\beta\)，\(g_{12}\)表示反馈网络的内部反馈。

为了方便求出该电路，首先将所有环路“单向化”，既去掉前馈网络和反馈网络的内部反馈，令\(G_{12}=g_{12}=0\)。在输入环路使用KVL，在输出节点使用KCL。

\[V_{in}=V_e+g_{22}{V_e\over{Z_{in}}}+g_{21}V_{out}\tag{8.12} \]

\[g_{11}V_{out}+{V_{out}-A_0V_e\over{Z_{out}}}=0\tag{8.13} \]

求得闭环增益，并表示为熟悉的形式\(A_{v,open}/(1+\beta{A_{v,open}})\):

\[A_{v,close}={V_{out}\over{V_{in}}}={{A_0\over{(1+{g_{22}\over{Z_{in}}})(1+g_{11}Z_{out})}}\over{1+g_{21}}{A_0\over{(1+{g_{22}\over{Z_{in}}})(1+g_{11}Z_{out})}}}\tag{8.14} \]

则开环增益和反馈系数可以表示为：

\[A_{v,open}={A_0\over{(1+{g_{22}\over{Z_{in}}})(1+g_{11}Z_{out})}}\tag{8.15} \]

\[\beta =g_{21}\tag{8.16} \]

可以看出，开环增益缩小了\([(1+{g_{22}\over{Z_{in}}})(1+g_{11}Z_{out})]^{-1}\)倍，相当于\(A_0\)乘以系数\({Z_{in}/(Z_{in}+g_{22})}\)和\(g_{11}^{-1}/(g_{11}^{-1}+Z_{out})\)，可以发现两系数表现为分压器的形式，因此加载效应可以体现为以下形式：

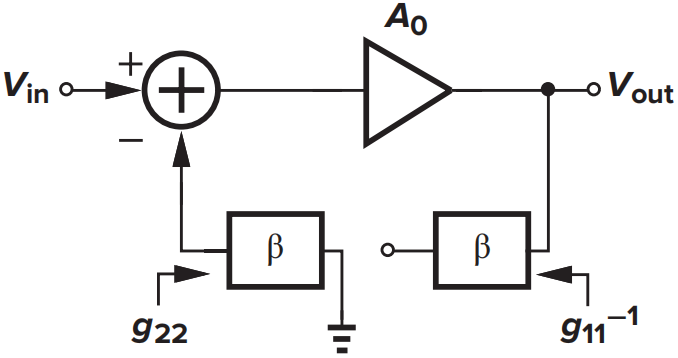
image-20200814143306949

其中，\(g_{11}\)可以通过反馈网络输出开路得到，\(g_{22}\)可以通过反馈网络输入短路得到。

  • 电路示例：
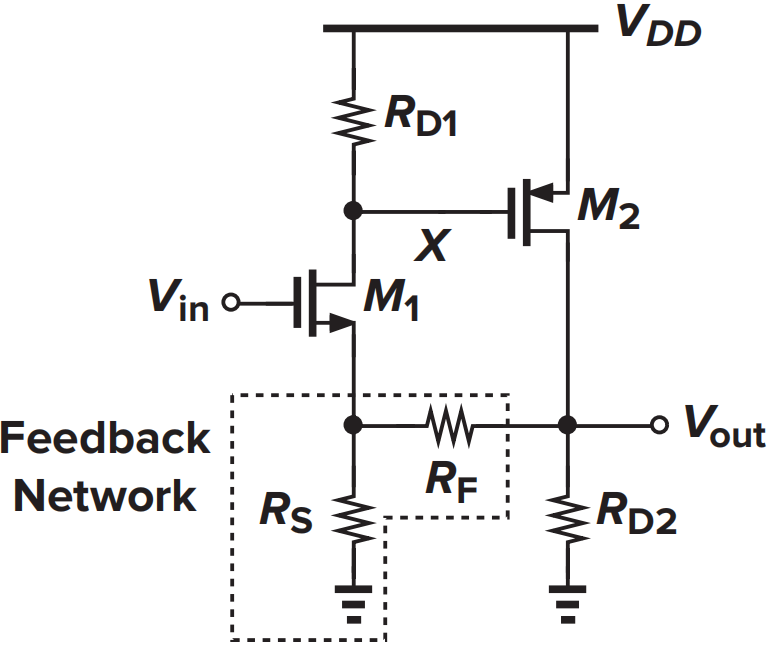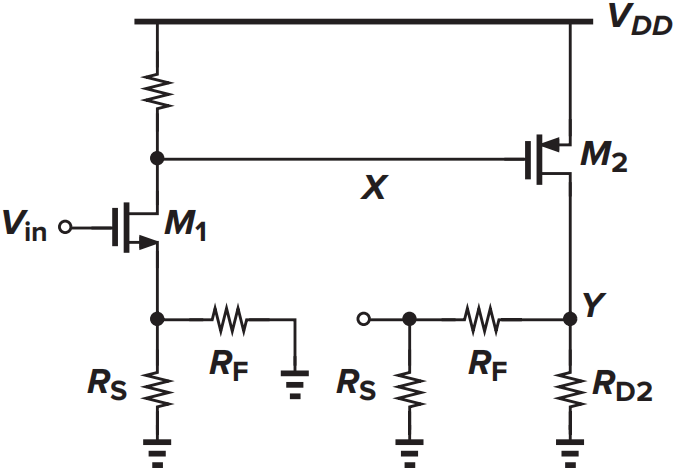image-20200814143348807 image-20200814143417294
原电路 考虑加载效应的开环电路

左图是原电路图，可以看出是电压-电压负反馈。右图是考虑了加载效应的开环等效图。则开环增益为：

\[A_{v,open}={V_Y\over{V_{in}}}={-R_{D1}\over{R_F||R_S+1/g_m}}\{-g_m[R_{D2}||(R_F+R_S)]\}\notag \]

由于\(A_{v,close}={A_{v,open}/(1+g_{21}A_{v,open})}\)，因此只需要找到\(g_{21}\)即可得到闭环增益。在电压-电压反馈考虑加载效应的模型中，关于\(g_{21}\)在反馈网络中有

\[V_{fb}=I_{fb}g_{22}+V_{out}g_{21}\notag \]

其中，\(V_{fb}\)为反馈网路的输出电压（位于前馈网络输入端），\(I_{fb}\)为反馈网络的输出电流。因此为了求得\(g_{21}\)，可令\(I_{fb}=0\)，此时在电路中求得

\[\beta=g_{21}={V_{fb}\over{V_{out}}}|_{I_{fb}=0}={R_s\over{R_s+R_f}}\notag \]

此时根据\(A_{v,close}={A_{v,open}/(1+g_{21}A_{v,open})}\)即可求得闭环增益。

电流-电压反馈

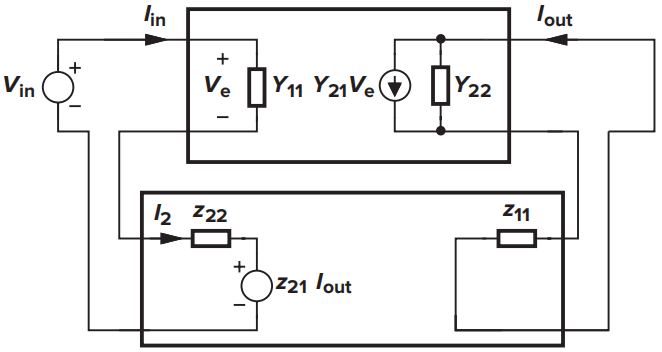
image-20200814143511146

电流-电压反馈前馈网络采用Y参数进行建模，反馈网络采用Z参数。这是由于前馈网络的输入为电压信号，输出为电流信号，因此前馈网络的增益为跨导量纲；而反馈信号的输入为电流信号，输出为电压信号，增益为阻抗量纲。

电流-电压反馈的加载效应可以体现为以下形式：

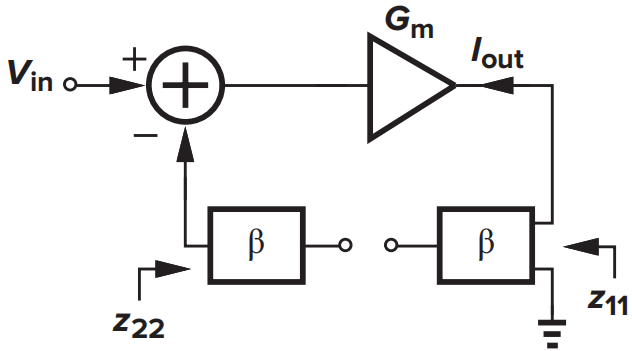
image-20200814143537641
  • 电路示例：
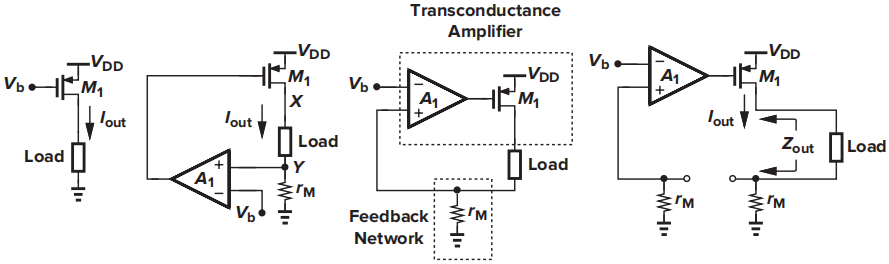
image-20200814143635761

开环增益计算为：

\[G_{m,open}={I_{out}\over{V_b}}\approx{A_1g_m}\notag \]

反馈系数\(z_{21}\)可由\(I_2=0\)条件下求得

\[\beta=z_{21}={V_{fb}\over{I_{out}}}|_{I_2=0}=r_M\notag \]

则闭环输出电流为

\[I_{out}={A_1g_m\over{1+A_1g_mr_M}}V_b\notag \]

开环时的负载看到的阻抗为\(r_O+r_M\)，反馈调节了输出电流使输出阻抗提高了\(A_1g_mr_M\)倍，为

\[Z_{out}=(1+A_1g_mr_M)(r_O+r_M)\notag \]

使得该电路更接近理想电流源。

电压-电流反馈

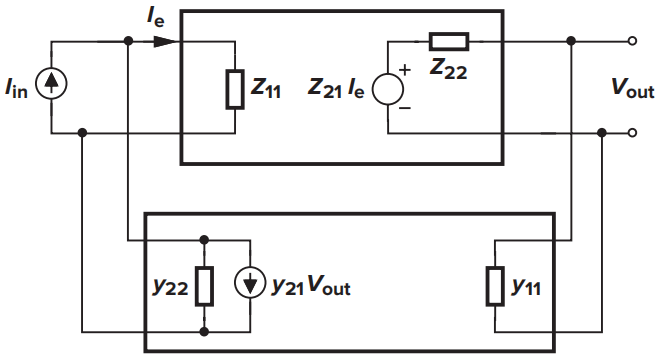
image-20200814143713625

电压-电流反馈前馈网络采用Z参数进行建模，反馈网络采用Y参数进行建模。加载效应可表现为以下形式：

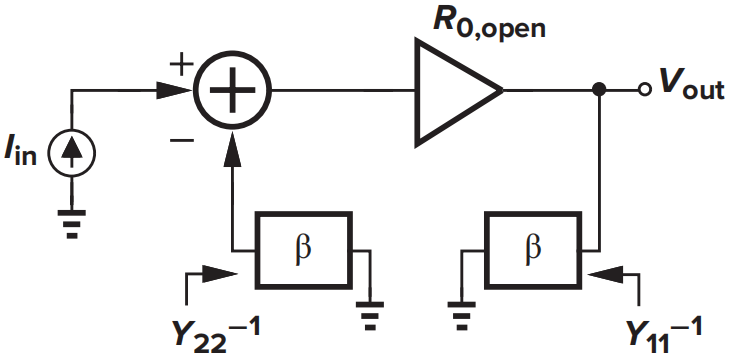
image-20200814143903282
  • 电路实例：
image-20200814144010135

开环增益可通过考虑加载效应的开环等效电路图得到

\[R_{0,open}=-R_Fg_m(R_F||R_D)\notag \]

反馈系数\(y_{21}\)可由\(I_{fb}=V_{fb}y_{22}+V_{out}y_{21}\)当\(V_{fb}=0\)时求得：

\[\beta=y_{21}={I_{fb}\over{V_{out}}}|_{V_{fb}=0}=-{1\over{R_F}}\notag \]

则闭环增益\(R_{0,close}\)为

\[R_{0,close}={V_{out}\over{I_{in}}}={R_{0,open}\over{1+\beta R_{0,open}}}={-R_Fg_m(R_F||R_D)\over{1+g_m(R_F||R_D)}}\notag \]

电流-电流反馈

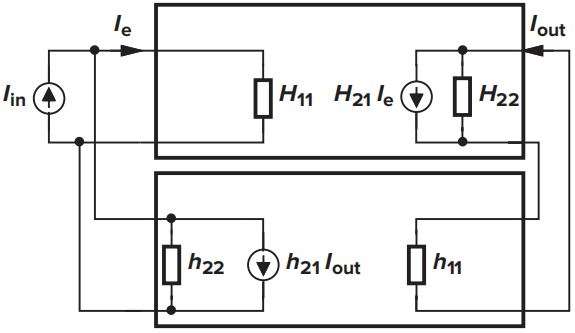
image-20200814145447194

电流-电流反馈前馈网络和反馈网络都属于电压放大器模型，都是用H模型进行建模。其加载效应如下所示：

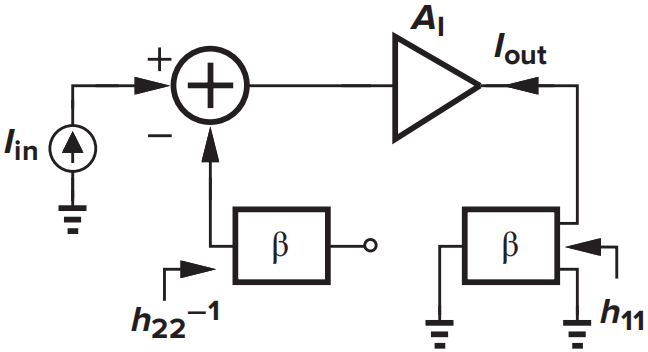
image-20200814145631107
  • 电路实例：
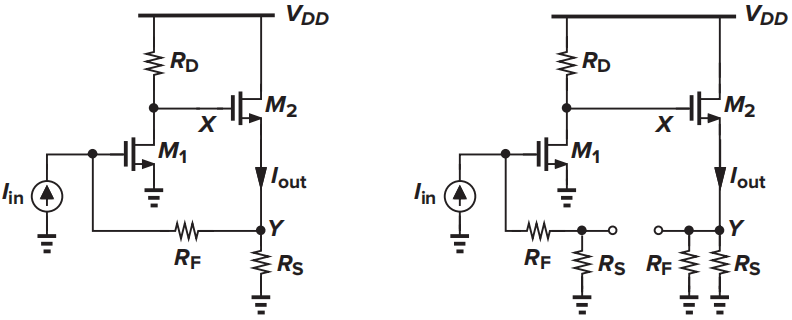
image-20200814145741315

开环增益为：

\[A_{i,open}={I_{out}\over{I_{in}}}={-(R_F+R_S)g_{m1}R_D{1\over{R_S||R_F+1/g_{m2}}}}\notag \]

反馈系数由\(I_{fb}=V_{fb}h_{22}+I_{out}h_{21}\)得到：

\[\beta={h_{21}}={I_{fb}\over{I_{out}}}|_{V_{fb}=0}=-{R_S\over{R_F+R_S}}\notag \]

则可由\(A_{i,close}={A_{i,open}/(1+\beta A_{i,open})}\)求得闭环增益。

加载效应小结

四种反馈结构的加载效应开环等效如下表所示：

image-20200814143306949 image-20200814143537641
电压-电压反馈 电流-电压反馈
image-20200814143903282 image-20200814145631107
电压-电流反馈 电流-电流反馈

计算闭环增益的步骤为：

  1. 画出相应电路包含加载效应的开环等效电路图；
  2. 根据等效图计算开环增益\(A_{open}=OUT/IN\)，此时求得的开环增益包含了加载效应的影响；
  3. 计算反馈系数\(\beta\)，根据使用的等效参数模型（Z，Y，G，H）的等式来求得反馈系数；
  4. 根据得到的\(A_{open}\)和\(\beta\)即可求得环路增益\(LP=\beta A_{open}\)和闭环增益\(A_{close}=A_{open}/1+{\beta A_{open}}\)；
  5. 求系统的输入/输出阻抗。根据等效电路图先求得开环时的输入/输出阻抗，然后根据反馈类型和环路增益可以求得闭环时的输入/输出阻抗。

二端口等效的优势与局限

优点 缺点
计算开环增益时包含加载效应 忽略了前馈效应(可能会忽视零点)
能较为简单且精确地求得环路增益和闭环增益 不能应用于非规范结构
可以递归地应用于多重反馈机制 -

波特法

波特法原理与意图

详见拉扎维第二版282~286页。

波特分析

波特分析中需要计算A，B，C，D四个系数。以具体电路为例：

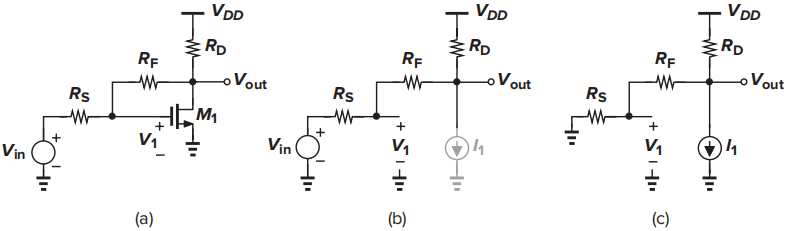
image-20200814162928891

图(a)为原始电路，为了求得A，C系数，将电路中的一个受控源去掉，得到了图(b)；为了求得B，D系数，将输入信号置零，得到了图(c)。

受控源为0 输入信号为0
$$A={V_{out}\over{V_{in}}}={R_D\over{R_D+R_S+R_F}}$$ $$B={V_{out}\over{I_1}}=-{R_D(R_S+R_F)\over{R_D+R_S+R_F}}$$
$$C={V_1\over{V_{in}}}={R_F+R_D\over{R_D+R_S+R_F}}$$ $$D={V_1\over{I_1}}=-{R_SR_D\over{R_D+R_S+R_F}}$$

  • 环路增益：\(LP=-g_mD\)

  • 开环增益：\(A_{open}\approx g_mBC\)(不精确的等效)

  • 闭环增益：\(A_{close}=A+{g_mBC\over{1-g_mD}}={A+g_m(BC-AD)\over{1-g_mD}}\)

\(-g_mD\)还可被称作返回比(RR)，表示环路增益。

布莱克曼阻抗定理(Blackman’s theorem)

该定理采用与波特方法类似的计算形式，用来计算所关心端口的阻抗。

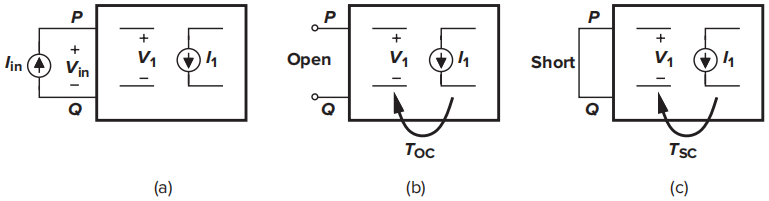
image-20200814185153318

由图(a)引出

\[V_{in}=AI_{in}+BI_1\tag{8.17} \]

\[V_1=CI_{in}+DI_1\tag{8.18} \]

则端口阻抗为

\[Z_{in}={V_{in}\over{I_{in}}}=A+{g_mBC\over{1-g_mD}}\tag{8.19} \]

为了获得更加直观的表达式，我们将公式变形。首先，由式\((8.18)\)可得，当\(I_{in}=0\)时\(V_1/I_1=D\)，我们称\(-g_mD\)为“开路环路增益”，并以\(T_{OC}\)表示；在式\((8.17)\)中令\(V_{in}=0\)，则可得到\(I_{in}=(-B/A)I_1\)，将该式带入\((8.18)\)中即可得到\(V_1/I_1={(AD-BC)/A}\)，我们将该量乘以\(-g_m\)称为“短路环路增益”，并以\(T_{SC}\)表示。

\[T_{OC}=-g_m{V_1\over{I_1}}|_{I_{in}=0}\tag{8.20} \]

\[T_{SC}=-g_m{V_1\over{I_1}}|_{V_{in}=0}\tag{8.21} \]

将\(Z_{in}\)用\(T_{OC}\)和\(T_{SC}\)表示为

\[Z_{in}=A\:{1+T_{SC}\over{1+T_{OC}}}\tag{8.22} \]

  • 电路实例：
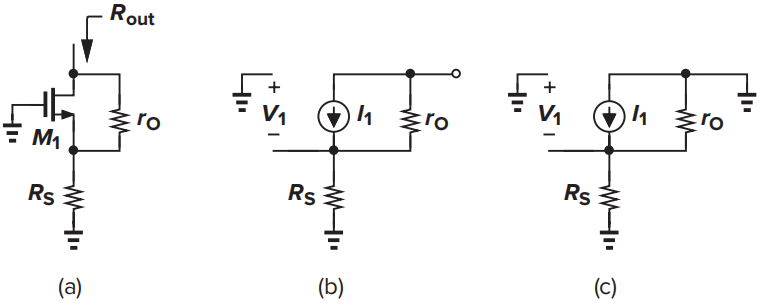
image-20200814202234289
  1. 计算\(A\)，将晶体管受控源禁用，有：

\[A={V_{out}\over{I_{out}}}|_{I_1=0}=r_O+R_S\notag \]

  1. 计算\(T_{OC}\)，将所关心的端口开路，有：

\[T_{OC}=-g_m{V_1\over{I_1}}|_{I_{out}=0}=0\notag \]

  1. 计算\(T_{SC}\)，将所关心的端口短路，有：

\[T_{SC}=-g_m{V_1\over{I_1}}|_{V_{out}=0}=+g_m(R_S||r_O)\notag \]

  1. 计算端口阻抗\(R_{out}\)，有：

\[R_{out}=A\:{1+T_{SC}\over{1+T_{OC}}}=(1+g_mr_O)R_S+r_O\notag \]

环路增益计算

计算环路增益时常常会断开环路进行计算，而断开环路的位置不同可能会导致加载效应。以下是断开环路并插入测试源的一些建议

  • 如果希望注入电压：在MOS管栅极断开环路，一端注入测试电压，在另一端得到输出电压；

  • 如果希望注入电流：替换MOS管的受控源，在MOS栅极得到输出电压，此时环路增益为\((-V_{GS}/I_1g_m)\)。

使用返回比RR计算时可能会遇到一种情况：系统中的晶体管(\(g_m\)级)不止一个，此时应该对哪个晶体管计算返回比呢？建议是

尽量不要破坏系统中存在的反馈

波特法的另一种解释

增益渐进形式

已知闭环增益为\(A_{close}=A+{g_mBC/{1-g_mD}}\)，禁用受控源时，即\(g_m=0\)时\(A_{close}=A\)；当受控源非常强，即\(g_m\rightarrow\infty\)，则\(A_{close}=A-BC/D\)。我们将\(g_m=0\)时的闭环增益称为\(H_0\)，可以理解为直接馈通增益，将\(g_m\rightarrow\infty\)时的闭环增益称为\(H_{\infty}\)，可以理解为理想增益。令\(T=-g_mD\)，则可得到闭环增益的增益渐进形式：

\[A_{close}=H_{\infty}{T\over{1+T}}+H_0{1\over{1+T}}\tag{8.23} \]

电路实例：

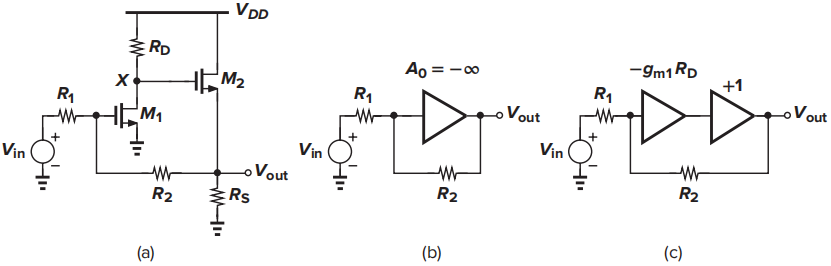
image-20200815105200740

图中存在两个MOS管，即存在两个受控源。选择\(M_1\)作为受控源，当\(g_{m1}=0\)时，有

\[H_0={(1/g_{m2})||R_S\over{(1/g_{m2})||R_S+R_1+R_2}}\notag \]

当\(g_{m1}=\infty\)时，有

\[H_{\infty}=-{R_2\over{R_1}}\notag \]

令输入\(V_{in}=0\)，用独立源\(I_1\)替换\(M_1\)的受控源，计算\(T_1\)

\[T_1=g_mR_D{g_{m2}[R_S||(R_1+R_2)]\over{1-g_{m2}[R_S||(R_1+R_2)]}}{R_1\over{R_1+R_2}}\notag \]

双零值方法

根据布莱克曼阻抗定理，我们可以考虑将传输函数也写作\(Z_{in}=V_{in}/I_{in}=A(1+T_{SC})/(1+T_{OC})\)的形式，即将阻抗中的\(V_{in}\)替换为增益计算时的\(V_{out}\)，将阻抗中的\(I_{in}\)替换为增益计算的\(V_{in}\)，我们将增益表示为

\[A_{close}={V_{out}\over{V_{in}}}=A{1+T_{out,0}\over{T_{in,0}}}\tag{8.24} \]

其中，\(T_{out,0}\)表示\(V_{out}=0\)时的返回比，\(T_{in,0}\)表示\(V_{in}=0\)时的返回比。

注意满足\(A\neq 0\)才能使用双零值方法。

波特法优势与局限

优点 缺点
不用断开环路就能计算闭环增益 只存在一种反馈机制时才能得到环路增益
可以应用于任意结构 -

麦德布鲁克方法

利用“分离定理”，在不断开环路的情况下能得到闭环传输函数，并且包含非单向环路的影响。

详情见拉扎维第二版8.7小节(也是较为简单的描述)，以后有需要再做补充。

posted @ 2020-08-10 11:05  Harroy  阅读(5674)  评论(0)  编辑  收藏  举报