Slope Trick

更新日志

2024/12/25-2024/12/26：开工。（半夜写的，跨了一天）

2024/12/16：完善、修正。

鸣谢这篇CF博客

---

前置知识

这部分内容都不会证明，如有缺漏，请自行搜索。

1. 动态规划，优先队列等编程基础知识
2. 函数的凸性、凸性的转移、分段函数概念、斜率等函数基础知识

概念

请注意，Slope Trick 并不是我们通常说的斜率优化。

Slope Trick本质上是一种优化DP的方式，其中DP方程函数图像通常满足如下性质：

是一个凸连续分段函数，其中每一段均为一次函数。同时，每一段的斜率为整数。
*连续：相邻两段函数的端点重合。
*凸：每段函数斜率具有单调性。

且这个问题是最优化问题。

Slope Trick就可以借助这个函数图像来优化 \(O(n^2)\) 的DP。

基础知识

维护函数图像

首先，你暂时不用知道为什么要维护函数图像，在这里我们先给后续算法内容作铺垫。

我们已知这个函数是凸连续分段函数，且每一段的斜率均为整数。那么，我们可以储存分界点。举个例子：

\[f(i)=|i|\\ \Leftrightarrow f(i)=\begin{cases}i,i\ge0\\-i,i<0\end{cases} \]

这个函数具有唯一一个分界点 \(0\)。

下面我们考虑如何维护斜率。假定我们已知最右段函数的斜率与最右分界点的函数值，那么我们可以用分界点的数量来表示分界点右侧段到左侧段的斜率变化量。

仍以 \(f(i)=|i|\) 为例，我们已知最右段函数 \(f(i)=i\) 斜率为 \(1\)，我们将这个函数储存为数列 \(\{0,0\}\)。

这个例子可能不是很通用，我们考虑以下分段函数：

\[f(i)=\begin{cases}-3i,i\le 0\\i,0<i\le1\\2i-1,1<i\le3\\5i-10,3<i\end{cases} \]

那么我们表示这个函数的数列就是 \(\{0,0,0,0,1,3,3,3\}\)。

同时，函数最右段斜率为 \(5\)，最右分界点的函数值为 \(5\)。

为了更快速地维护分界点的位置关系，所以我们往往会使用优先队列储存分界点数列。

解题思路

通常情况下，我们可以用如下思路解决Slope Trick问题。

获取 \(O(n^2)\) DP转移方程 \(\rightarrow\) 绘制函数图像找规律 \(\rightarrow\) 通过 Slope Trick 解决！

单调函数

解决思路

在讲解凸函数之前，让我们从单调函数入手——也就是半个凸函数。

题目大意：给定一个长度为 \(n\) 的序列 \(a\)，请你构造一个长度为 \(n\) 的单调不降序列 \(b\)，最小化 \(\sum|b_i-a_i|\)，输出这个最小值。
题目链接

我们轻易得到DP方程，\(f_i(j)\) 表示对前 \(i\) 个数构造符合条件的 \(b\) 且 \(b_i=j\) 的最小代价：

\[f_i(j)=\min_{k\le j}f_{i-1}(k)+|a_i-j| \]

我们发现这个函数是一个凸连续分段函数。

证明：
凸：首先 \(\min_{k\le j}f_{i-1}(k)\) 是凸函数，\(|a_i-j|\) 也是凸函数，两个凸函数相加也是凸函数，实现上只需要合并两个函数的分界点集即可。
连续：显然。
分段：显然。
函数：显然。

事实上，我们为了方便转移，我们实际储存的是函数 \(g_i(j)=\min\limits_{k\le j}f_i(k)\) 的函数图像。易证 \(g_i\) 是单调递减的，同时也是凸连续分段函数。

那么我们就可以使用上面所讲的方法来维护这个函数了。

借图CF博客：

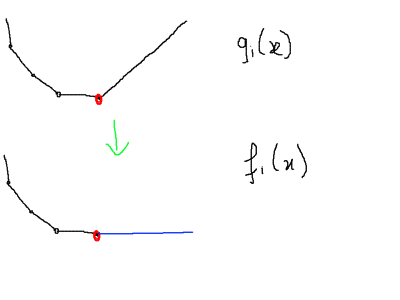
（我的讲解中 \(f_i\) 与 \(g_i\) 与上图相反，值得注意。）

而我们分界点表示法额外储存的两个信息分别是最右段斜率和最右侧节点的函数值。

对于 \(g_i\) 函数，最右端斜率固定，必然为 \(0\)，所以我们只需要动态维护最右侧节点的函数值与分界点数列即可维护整个函数。

不难发现，最后的答案就是 \(g_n(+\infty)=g_n(X)\)，\(X\) 为最右侧分界点。

那么，如何快速动态维护最右分界点的函数值与分界点数列，就成了最后的问题。

维护函数

我们考虑如何使用 \(g_{i-1}\) 更新 \(g_i\)。

我们先解决 \(f_i\) 吧。

更新 \(f_i\)

不难发现，\(f_i\) 函数其实就是 \(g_{i-1}\) 函数加上 \(|x-a_i|\) 函数。

\(|x-a_i|\) 函数的分界点数列为 \(\{a_i,a_i\}\)，这个很显然。

合并这两个函数分为三步：

• 合并分界点，直接把 \(\{a_i,a_i\}\) 加入 \(g_i\) 函数地分界点数列即可。
• 更新最右分界点函数值。若 \(a_i\) 位于当前最右分界点左侧，那么最右分界点函数值会加上 \(X-a_i\)。否则，\(a_i\) 成了新的最右分界点，函数值不变（\(|x-a_i|=0\)）。
• 更新最右段函数斜率，加上 \(|x-a_i|\) 最右段函数斜率即可。

事实上，我们无需更新 \(f_i\)，写这一步主要是为了方便理解。真正的更新方式将会在更新 \(g_i\) 部分给出。

更新 \(g_i\)

还是同一张图，\(f,g\) 也还是反的。

很简单，直接给出变化结论：所有斜率大于 \(0\) 的函数都会被拉平。

下面告诉你一个事实：完全没有储存 \(f_i\) 的必要，我们可以直接通过 \(g_{i-1}\) 更新 \(g_i\)。

首先最右端函数斜率肯定固定为 \(0\) 了，我们无需储存这个东西。

这时最右分界点右侧函数的斜率必须是零，\(g_{i-1}\) 满足这个性质，我们正在构造的 \(g_i\) 同样必须满足这个性质。

先罗列一下大致步骤：

1. 合并分界点集合。
2. 更新最右分界点。你会发现合并集合后，可能会有一些分界点因为拉平操作而不存在了，这些分界点右侧的函数斜率均大于零。怎么维护下面着重讲解。
3. 更新最右分界点函数值。这个必须在更新最右分界点后完成，所以也在下面一起讲解。

更新最右分界点

我们每插入一个分界点，最右分界点就（可能）会变化一次，所以我们实时更新最右分界点。

我们会发现一个令人为难的问题，加入的这个分界点，**到底是让他左侧的斜率 \(-1\)，还是让他右侧的斜率 \(+1\)？

这个问题在绝对值函数这种只有两个相等的分界点的时候还不是很重要，但当这个分段函数的分界点增多时，就会造成意外的影响。例如第一道练习题。

我们定义原函数中左侧斜率 \(<0\) 的分界点为负分界点，右侧斜率 \(>0\) 的分界点为正分界点。首先分界点非负即正，因为每个分界点都代表 \(1\) 的斜率变化量。不难发现，在合并时，负分界点使被合并函数左侧斜率 \(-1\)、右侧斜率 \(+1\)。

这个很好证明的，就不作额外证明了。实在不行感性理解即可。事实上你只需要想明白合并分界点、合并斜率表现在函数图像上到底是啥变化就行了。

值得注意的是，如果正负分界点同时作用于一个点，那么正分界点在右。这个很显然吧。

为什么要思考这个问题？你会发现，只有正分界点会更新最右分界点（指使其斜率大于 \(0\)），而负分节点不会（当然它自己可能成为新的最右分界点）。

请不要忽略上面引用的内容，它很重要。下面回归正题：

我们每次加入正分界点时，此时整个函数最右段斜率必然为 \(1\)，那么就应该把这一段拉平，也就是删除最右分界点，使次右分界点成为最右分界点。

至于负分节点，直接加入集合即可，它不会影响最右段函数斜率（但可能把最右段函数分成两段，但新最右段斜率仍不变）。

这时候我们就会发现，我们不能直接顺次合并分界点。

本质上来说，我们是给整个函数完成合并之后，再依次删除右侧斜率 \(>0\) 的分界点的。但是，新合并进去的分界点也有可能成为过要被删除的最右分界点。所以，我们需要按坐标从大到小加入分界点，这样所有会成为最右分界点的新合并分界点，在被后续可能会影响他的正分界点更新操作之前，都会在正确的位置上。

对于例题，这个要求并不显然，所以我选择的练习就有这方面的要求。

更新最右分界点函数值

我们考虑什么时候最右分界点函数值会发生变化，肯定是最右分界点变化的时候啊。

所以只需要在更新最右分界点的时候更新最右分界点函数值就行了。

我们发现，加上这个函数值之后，此时（删除最右分界点之前）最右分界点与次右分界点之间斜率为 \(0\)，二者值相等，所以我们可以计算原最右分界点的新值得到新最右分界点的值。

我们本来就知道原最右分界点的值，给他加上我们添加的函数对应值即可。

至此我们就解决了合并问题。

边界问题

注意，在例题中，并没有限制 \(b\) 的构造范围，并且假如 \(b\) 超出值域必然不优。

但有时候可能会出现越界的情况，这时候请注意手动更新边界分界点。

详见凸函数的练习题

示例代码

这里将会给出一份，完全符合上述逻辑，不带任何简化且能AC的代码。

网络上有很多代码，但都是针对于绝对值函数的，有时候那些简化会丧失真正合并的逻辑。

代码当然是例题的，只包含关键部分。

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n;
    rep(i,1,n){
        cin>>a[i];
        //现在想象一个绝对值函数，一个负分界点，和一个正分界点。二者重合。
        pq.push(a[i]);//加入正分界点
        ans+=pq.top()-a[i];//删除最右分界点并更新最右分界点函数值。此时最右分界点必然>=a[i]，无需加绝对值。
        pq.pop();
        pq.push(a[i]);//加入人畜无害的负分界点。
    }
    cout<<ans;
    return 0;
}

构造方案

理论证明

我们发现，\(g_i\) 是前 \(i\) 个数构成的前缀的全局最优解。

观察方程式，以例题为例：

\[f_i(j)=\min_{k\le j}f_{i-1}(k)+|a_i-j| \]

所以当 \(f_i\) 最优时，只需要让 \(f_{i-1}\) 在满足 \(f_i\) 最优的情况下最优即可。

首先我们存的是 \(g_i\)，但我们可以确定最右分界点的 \(f\) 必然等于 \(g\)，所以直接取最右分界点即可。

然后考虑粗体字的意思，因为局部最优不一定全局最优，所以又是二者会出现矛盾。表现在凸函数上，就是斜率为 \(0\) 的函数段左端点大于 \(b_{i+1}\)，也就是不符合单调性。这时候就需要先服从全局最优，然后使局部最优。发现它单调递减，所以尽可能靠右，也就是取 \(b_{i+1}\) 时最优。

能这么倒推的唯一原因是我们已知每个 \(i\) 前缀最优解以及其对应的一个可行 \(b_i\)。

公式证明

\[f_i(j)=\min_{k\le j}f_{i-1}(k)+|a_i-j| \]

现在，对于每一个 \(f_i\)，我们都可以知道 \(\min\limits_{k\le j}f_i(j)\)（要么在最右段，要么取不到，尽可能靠右），并且知道值为这个最小值的一个下标（最右分界点的 \(f\) 函数值必然为最小值），所以我们可以递归构造每一个函数。我们知道 \(b_{i+1}\)，那么就知道此时 \(i\) 的答案就是 \(\min\limits_{k\le b_{i+1}}f_i(k)\)，并且也可以得到这个范围内的最优决策点。

另一种统计答案的方法

然后你会发现，你得到了另一种无需实时计算最右分界点答案的答案统计方法，就是构造完 \(b\) 之后直接统计即可。

过于简单，不给代码示例了。

练习

花火

显然可以按 \(t\) 排序，要求构造答案最小的单调不降的距离数列。

但你会发现，同一时间内，人只能在一个位置。

所以说，这道题中数列，其实不是按花火个数的，是按照时间个数的。

那么这时候，转移方程也就没这么简单了：

\[f_i(j)=\min_{k\le j}f_{i-1}(k)+\sum_{k}^{time_k=i}|p_k-j| \]

然后毫无疑问的，最右边那一坨还是个凸函数，直接上就行。

但这时候它的分界点就没有在同一位置了，如何合并详见上面解释的部分。

那么还有一个问题，怎么知道分界点的正负呢？

观察发现，他就是多个绝对值函数合并，那么事实上每个分界点和它原来在绝对值函数内的正负是一致的。当然你会发现如果重新统计这个复合函数的所有分界点正负，也是对的。

那么就解决了这个问题。

提交记录

凸函数

解决思路

凸函数就是两个单调函数，对，维护两个单调函数就行了。所以本质上是没有什么不同的。

通常情况下，左右两部分都会视情况产生一定的偏差量，听起来有些抽象，这取决于具体题目——所以我仍然会根据例题讲解。

例题

首先给出状态转移方程，这应该不用介绍了吧。

令 \(len\) 为这一段的长度，\(r\) 为右端点坐标。

\(f_i(j)\) 表示把第 \(f_i\) 个的右端点坐标移到 \(j\) 的最小总代价。

\[f_i(j)=\min_{k\in[j-len_i,j+len_{i-1}]}f_{i-1}(k)+|r_i-j| \]

其实有个固定的规律，但你没必要死记，每次上手画几个图就能出来：

假如那个 \(\min\) 的区间为 \([j-A,j+B]\)

每更新一次，左侧单减函数所有分界点左移 \(B\)，右侧单增函数所有分界点右移 \(A\)。

如果是上凸函数，也可以推出类似的规律，不过多介绍。

可以用两个懒标记存此时左右两侧分界点的位移。

知道了这个你就基本解决了大多数 Slope Trick问题。但别急，还有东西没讲。

维护函数

这时候你发现，负作用点不再人畜无害了，正作用点也不一定必然有影响了。

它们是否起作用，取决于它们当前所在的位置，究竟是在单减函数，还是单增函数。维护细节与单调函数是一致的。

另外，如果一侧的最右（右边是最左）分界点代表斜率大于 \(0\)，弹出时把它弹到另一边去。

这时候我们会发现，对于队列中每一个分界点，我们都会认为其值为 \(x+\Delta_i\)，所以，我们每次插入时，假如当前偏移量为 \(\Delta_j\)，真实坐标为 \(x\)，我们加入 \(x-\Delta_j\)。这样后续对于这个节点的偏移量就是 \(\Delta_i-\Delta_j\)，就正确了。

同时，这样维护，队列里的位置顺序也是正确的。显然。

边界问题

这道例题中，首先没有边界要求，其次越界必然不优。

但，如果有边界限制呢？

详见第二道练习题。

示例代码

关键部分，以及代码注释。

grheap<ll> lft;//大根堆
lrheap<ll> rgt;//小根堆
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n;
    rep(i,1,n){
        cin>>l[i]>>r[i];
        l[i]=r[i]-l[i];//直接把l改成长度，更方便些。
    }
    lft.push(r[1]);rgt.push(r[1]);//初始化，两个作用点一左一右。
    rep(i,2,n){
        dtl+=l[i-1];dtr+=l[i];
        if(r[i]<lft.top()-dtl){//在左侧
            lft.push(r[i]+dtl);//加入正作用点
            ans+=lft.top()-dtl-r[i];//更新答案
            rgt.push(lft.top()-dtl-dtr);//把超出部分塞到另一边
            lft.pop();
            lft.push(r[i]+dtl);//加入负作用点
        }else if(r[i]>rgt.top()+dtr){//同理
            rgt.push(r[i]-dtr);
            ans+=r[i]-(rgt.top()+dtr);
            lft.push(rgt.top()+dtr+dtl);
            rgt.pop();
            rgt.push(r[i]-dtr);
        }else{
            //这时候绝对值函数落在了原斜率为 $0$ 的位置上，成为了新的最小值。发现答案更新值为0故省略。
            lft.push(r[i]+dtl);
            rgt.push(r[i]-dtr);
        }
    }
    cout<<ans;
    return 0;
}

练习

序列变换

你会发现，这道题就有边界要求了。

首先转移式就不写了，根据上面给出的规律推就行。

考虑向右越界情况（因为只会右移），若右侧函数越界，那么事实上无需更新答案，对斜率为零区间无影响。

但是，如果左侧函数越界，就需要想办法更新新的最右分界点函数值了。这一步细节很多，但其实不难，详见代码部分。

其实这题构造后更新答案更简单，但我写的是实时更新答案的方法，相对来说思维难度更大，但作为练习题可以尝试。

此外还要考虑一种情况，就是它可能会无法取到当前的最小值，也就是向左越界。

为什么呢？因为每个 \(b\) 都有下界要求，虽然当前的 \(b\) 没有越界，但你会发现，往回推几步，可能会出现从不存在的位置转移来的情况。这样会导致整个函数错误。

如何解决左侧越界问题？首先，整个函数的最小值必然是没有越界的（没有越界分界点影响的话），那么函数转移过来的位置越界只可能答案区间完全位于左侧单减函数部分，那么必然会优先向右取。所以，当前最优情况是伪的，就代表取值范围内最右侧点也越界了。

这时候我们发现一个细节，整个过程，我们真正在维护的，其实是最中间的斜率为零的区间。

所以，所有的越界，对于答案的唯一影响，就是当其错误地成为了斜率为零区间的边界的时候。我们只需要维护两个实际上不存在的位于合法边界的伪分界点即可，这样答案区间的两个边界就必然不会越界，所有越界分界点的影响也全都被屏蔽了。

提交记录