Reinforcement Learning: An Introduction读书笔记(3)--finite MDPs
> 目 录 <
- Agent–Environment Interface
- Goals and Rewards
- Returns and Episodes
- Policies and Value Functions
- Optimal Policies and Optimal Value Functions
> 笔 记 <
MDPs are meant to be a straightforward framing of the problem of learning from interaction to achieve a goal. The learner and decision maker is called the agent. The thing it interacts with, comprising everything outside the agent, is called the environment. These interact continually, the agent selecting actions and the environment responding to these actions and presenting new situations to the agent.1 The environment also gives rise to rewards, special numerical values that the agent seeks to maximize over time through its choice of actions.
More specifcally, the agent and environment interact at each of a sequence of discrete time steps, t = 0,1,2,.... At each time step t, the agent receives some representation of the environment's state, $S_{t}\in S$, where $S$ is the set of possible states, and on that basis selects an action, $A_{t}\in A(S_{t})$, where $A(S_{t})$ is the set of actions available in state $S_{t}$. One time step later, in part as a consequence of its action, the agent receives a numerical reward, $R_{t+1}\in R \subset \mathbb{R}$, and finds itself in a new state, $S_{t+1}$.
At each time step, the agent implements a mapping from states to probabilities of selecting each possible action. This mapping is called the agent's policy and is denoted $\pi_{t}(a|s)$ is the probability that $A_{t}=a$ if $S_{t}=s$. Reinforcement learning methods specify how the agent changes its policy as a result of its experience. The agent's goal, roughly speaking, is to maximize the total amount of reward it receives over the long run.
the actions are the choices made by the agent; the states are the basis for making the choices; and the rewards are the basis for evaluating the choices.
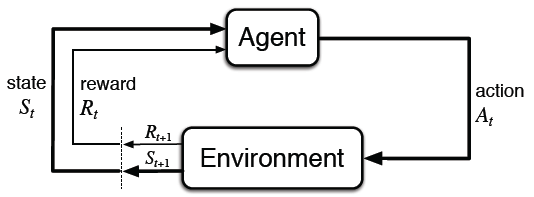
图1. agent-environment interaction in a MDP
马尔可夫性(Markov property): 如果state signal具有马尔科夫性,那么当前状态只跟上一状态有关,它包含了所有从过去经历中得到的信息。马尔可夫性对RL而言很重要,∵decisions和values通常都被认为是一个只跟当前state相关的函数。
MDP的动态性:$p(s',r|s,a)=Pr\left \{ S_{t}=s',R_{t}=r|S_{t-1}=s,A_{t-1}=a \right \}$,
where $ \underset{s'\in S \ r\in R}{\sum \sum}p(s',r|s,a)=1 $, for all $s\in S$, $a\in A(s)$.
基于the dynamics of the MDP, 我们可以很容易地得到状态转移概率(state-transition probabilities, $p(s'|s,a)$),state-action的期望回报(the expected rewards for state–action pairs, $r(s,a)$),以及state-action-next state的期望回报(the expected rewards for state–action-next state, $r(s,a,s')$)。
agent的goal是以一个从environment传递给agent的reward signal的形式存在的。我们通过定义reward signal的值,可以实现跟agent的交流,告诉它what you want it to achieve, not how you want it achieved。
Agent的目标是最大化total reward。因此,最大化的不是immediate reward,而是cumulative reward in the long run。
The return is the function of future rewards that the agent seeks to maximize (in expected value). return有多种形式,取决于task本身和是否希望对回报进行折扣。
Expected return: $G_{t}=R_{t+1}+R_{t+2}+...+R_{T}$, where T is a final time step。适合于episodic tasks。
Episodic tasks: each episode ends in the terminal state, followed by a reset to a standard starting state or a sample from a standard distribution of starting states.
Continuing tasks: the agent–environment interaction doesn’t break naturally into identifiable episodes, but goes on continually without limit.
Expected discounted return: $G_{t}=R_{t+1}+\gamma R_{t+2}+ \gamma ^{2}R_{t+3}+...=\sum_{k=0}^{\infty}\gamma ^{k}R_{t+k+1}$。其中,折扣率(discount rate, $\gamma$)决定了未来rewards的当前价值。适合于continuing tasks。
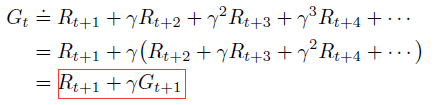
Value functions: functions of states (or state-action pairs) that estimate how good it is for the agent to be in a given state (or how good it is to perform a given action in a given state). The notion of “how good” here is defined in terms of future rewards that can be expected, or, in terms of the expected return from that state (or state-action pair).
Policy: a mapping from states to probabilities of selecting each possible action. If the agent is following policy $\pi$ at time t, then $\pi(a|s)$ is the probability that $A_{t} = a$ if $S_{t} = s$.
the value function of a state s under a policy $\pi$: (i.e. the expected return when starting in s and following $\pi$ thereafter)
We call the function $ v_{\pi}$ is the state-value function for policy $\pi$
the value of taking action a in state s under a policy $\pi$: (i.e. the expected return starting from s, taking the action a, and thereafter following policy $\pi$)
We call $ q_{\pi}$ the action-value function for policy $\pi$
Bellman equation for $v_{\pi}$: It expresses a relationship between the value of a state and the values of its successor states.
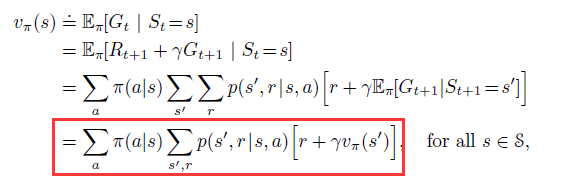
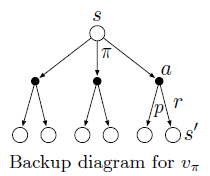
Optimal Policies and Optimal Value Functions
Value functions define a partial ordering over policies. $\pi> \pi'$ if and only if $v_{\pi}(s) > v_{\pi'}(s)$, for all $s \in S$. The optimal value functions assign to each state, or state–action pair, the largest expected return achievable by any policy.
Optimal policy $\pi_{*}$:A policy whose value functions are optimal. There is always at least one (can be many) policy that is better than or equal to all other policies.
Optimal state-value function:
Optimal action-value function:
用$v_{*}$来表示$q_{*}$:
Any policy that is greedy with respect to the optimal value functions must be an optimal policy. The Bellman optimality equations are special consistency conditions that the optimal value functions must satisfy and that can, in principle, be solved for the optimal value functions.
Bellman optimality equation for $v_{*}$:
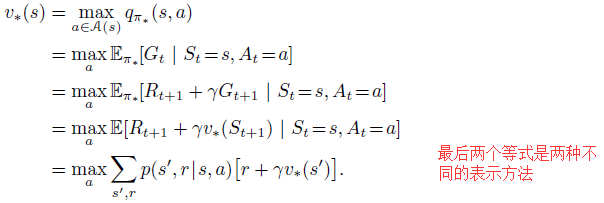
Bellman optimality equation for $q_{*}$:
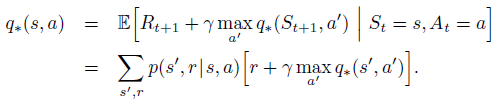
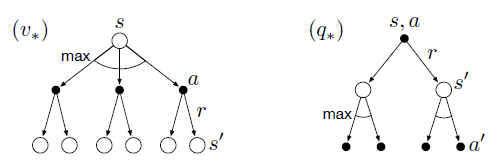
Backup diagrams for $v_{*}$ and $q_{*}$: