源自人脑的神奇算法 -- 读《How to make your own neural network》有感
最近读到了一本很好的关于机器学习-深度学习的书值得推荐下并特意做了这个学习总结。
为什么推荐
在我认为好书(计算机类)的评判有几个标准:
- 试图以通俗的语言阐述,并在引入任何新概念的时候都讲述来龙去脉,在无法详细展开的地方提供深入阅读的资料或者线索供读者自己去挖掘;
- 有易操作上手的实践;
- 没有明显的错误,花了足够的思考时间;
目前为止,我读到能符合上述标准的好书不多,例如深入理解计算机系统,汇编语言(王爽),再就是这本《如何从零开始构建神经网络》。
遇到这本书也是一种机缘,当下深度学习非常火热,作为后端工程师经常需要和机器学习工程师调试以及将他们的模型放入产品,所以也想了解下机器学习,不过我的角度和机器学习工程师不一样,我想理解机器学习的基本原理,之后再根据项目中用到的机器学习算法做个大概的了解就行了,因此这本书就被我挖了出来。
这本书试图以很少的先验知识,一步一步从理论和实践(基于python)帮助读者构建一个神经网络,几乎没有很跳跃的地方,读起来非常的爽快。
学习总结
什么是神经网络
大家都知道深度学习的本质依然是诞生了数十年的神经网络,只不过是多层的神经网络,这本书就试图揭示神经网络的基本原理。
首先有个问题,什么是神经网络? 书中引了一张人脑神经连接的图:
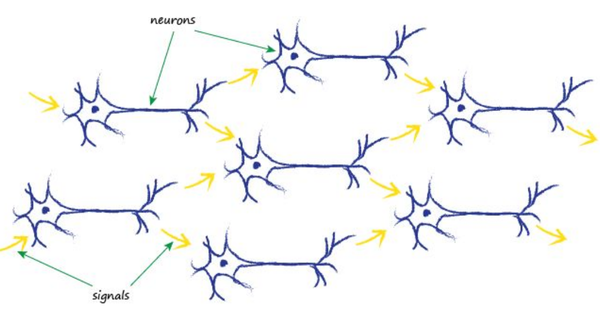
人脑由非常多的神经元构成,每个神经元可以看成是一个微小的计算单元,然后由许许多多计算单元最终构成人脑的计算,神经网络的灵感便来源于人脑,它也是将一个又一个的Node连接起来完成各种计算问题,下图是一个三层的全连接神经网络:
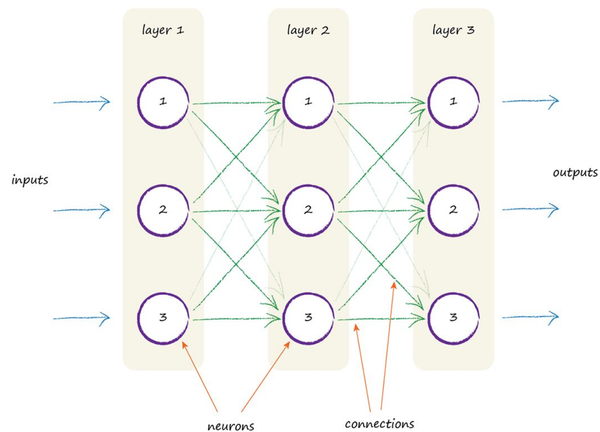
主要分为两个部分,Node(neurons)以及connections,两者合在一起构成了真正的神经网络。
那么为什么神经网络可以这么牛?我的理解是类似于计算机的基础组件:与非门,即便是很微小的计算单元,当组合在一起的时候依然可以发挥巨大的威力。
神经网络是如何计算的?
有了神经网络和给定输入怎么得到输出呢?也就是求值的过程是怎么样的?首先,很自然的想法是每一个connection都有一个weight,通过这些weight影响最终的结果,这样有任何一个连接就代表要把这个weight加入计算,于是我们便有了如下的计算公式:
公 式 1
其中X是中间层(也叫hidden)节点的输入,W是input到hidden的weight矩阵,I是输入向量,用加法而不是其他,是因为一个很简单的规则:越简单越好,如果简单的方法可以工作,就没有必要采取复杂的。
当然这里还没有完,科学家发现每一个神经元,其实内部还是有计算逻辑的,就是有一个触发机制,当输入信号很微弱的时候,神经元的输出会被抑制以至于没有输出,只有当信号超过一个阈值的时候才会触发输出,这个很好理解,就是过滤掉噪音。所以我们这里也有一个类似这样的过程,我们做一个映射并用一个函数来表示,这个函数叫activation function,大部分时候我们都采用如下函数,这个函数通常叫sigmoid function:
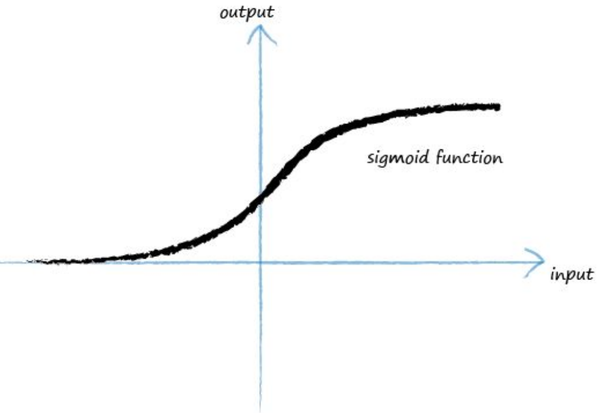
其函数表达式如下: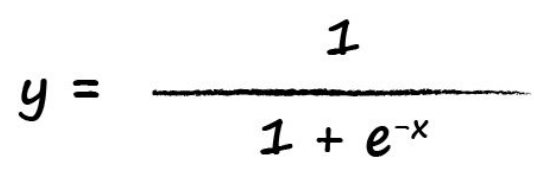
这个函数有一个特点,就是在0-1之间徘徊,且x只有超过一定的值,y才有显著的增加。
所以,我们对每一个内部节点的输入都会应用这个函数(如下图),从而产生输出,这个输出又会根据公式1去计算得到下一层的输入,如此往复直到最后一层的输出。
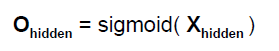
有了这个规则,我们就可以计算了,
神经网络的学习过程
这里有个问题就是weight怎么定呢?其实weights就是神经网络最核心的变量,而学习的过程就是最优化的求解weight的过程,我们把这个过程叫Back-propagation.对于神经网络来说,其目标函数就是最后一层的输出减去给定的正确值,我们得到了error。
公式 2
这里的求和是把最后一层的所有输出节点的错误累加,这个就是我们要优化的目标函数,我们选取怎么样的weight才能使得最终的错误最小?
大家都知道这个问题很困难,直接求解是非常复杂的,weight太多,同时还要算sigmoid,因此,大家发明了一种近似的方法来解决(这种近似的思路有很多应用,例如蒙特卡洛算法),这个就是传说中的Gradient Descent(梯度下降)!
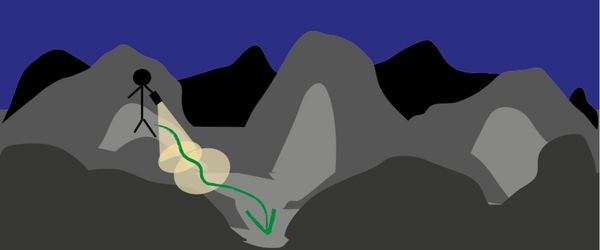
梯度下降本质上是一个很朴素的算法,但是取了一个听起来很厉害的名字,其思想可以用上图的下山例子来讲解:假设天黑了,你要独自一人下山,手里只有一个手电筒,你想最快的到达山底,会采用什么策略?一般情况下,会用手电筒环顾四周,选取一个斜率最大的下降坡走,因为这个时候下降的高度是最快的,这其实是一个贪心的策略,它的问题也很显然,容易陷入局部最优,不过这个可以用其他方法来解决。
同样对于一个很复杂的函数,我们甚至都不要太复杂的运算,只要不断的用梯度方向更新参数,就能够尽可能的逼近最优点,为了防止局部最优,我们可以采取多轮随机选取初始点的方法来避免。正是有了这个方法我们才能继续求解最佳的weight。
在求解前,有一个问题需要说清楚,那就是error的传递规则,类似于正向计算,error产生后,对于前一层的网络,其错误的计算应该按照weight切分错误,因为weight越大其对输出的错误贡献自然越大,然后只需要把输出的link上分担的错误累加即可求得当前节点的错误,如下图:
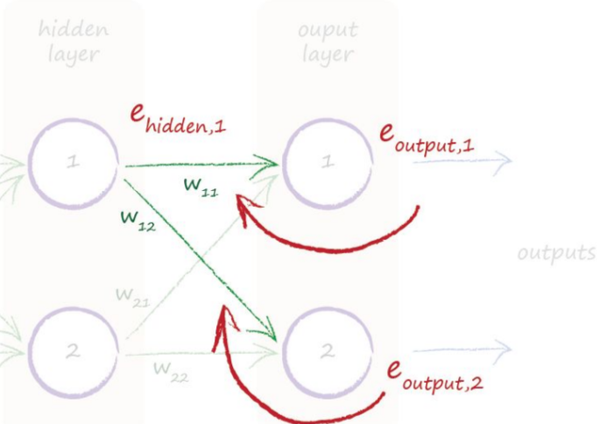
hidden layer节点1的错误应该是w11和w12分担的错误总和,所以有:
这个其实就是正向计算的逆向过程。
有了前面的这一系列铺垫,我们就可以正式开始学习(迭代求解weight的更新值)了,以下图的神经网络为例:
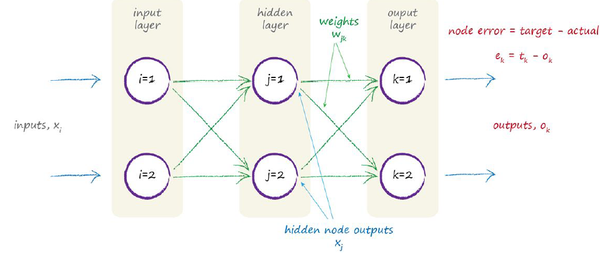
首先把目标函数列出来:

最右边是输出层的错误,假定我们要求进行更新,所以就要求它的偏导数来获得梯度下降方向。
基于事实:On的错误只和和它连接的weights有关,与不连接的weight无关,所以我们有:

因为我们是对求解,所以,只和输出层的节点k有关
学过高等数学的童鞋都知道偏导数的chain rule:
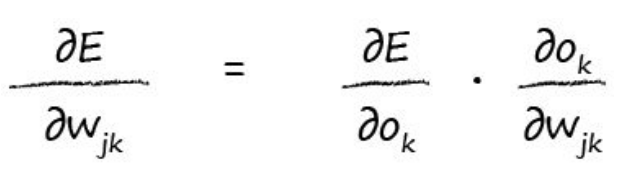
所以,我们可以应用这个公式继续展开:
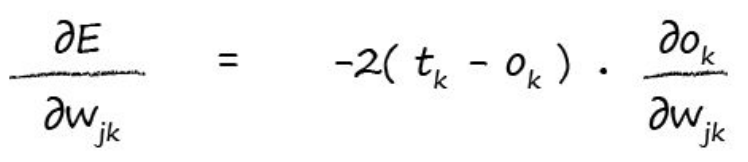
现在变成了Ok对求导,由公式1我们知道Ok是前面相关weights和节点输出的加和再算sigmoid,所以我们又可以展开Ok:
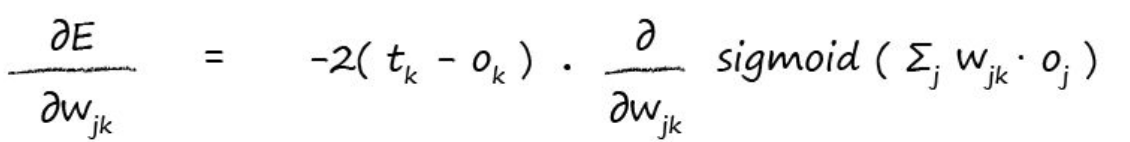
这里对sigmoid求导书中直接给出了结果,因为过程比较复杂:
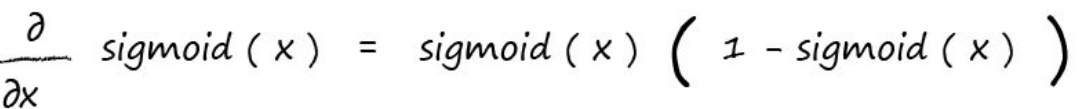
所以我们把sigmoid的求导函数应用上同时再加上chain rule,我们得到:
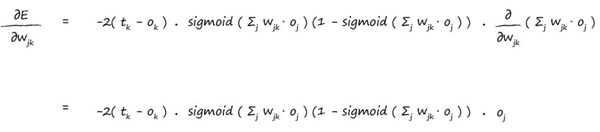
我们可以把-2抹掉,因为我们在乎的是方向而不是具体的向量长度,所以我们得到最终的结果如下:
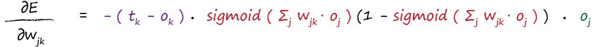
总结一下,对任意的梯度方向,它仅仅与几个因素有关:
- 输出节点Ok的错误值;
- Ok的值;
- Oj的值;
所以,每次迭代我们只需要按如下公式更新即可:
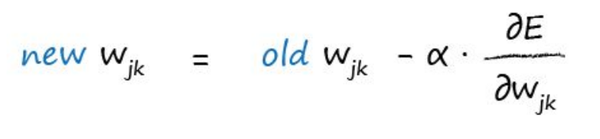
其中是learning rate,其实就是探索的步长,越大,我们找到谷底的速度越快,但是也有可能miss,例如直接跨过谷底了,导致无法收敛,所以也是一个需要调试的值。
用python实现简单的全连接神经网络
有了上面的理论基础,实现神经网络就变得很直接了,我自己也照着书弄了一遍,书中是用神经网络来做手写识别,代码比较简单,这里用了几个优化:
- 找到最优的learning rate;
- 多轮训练防止局部最优;
- 中间层的节点数的调整;
我实现的代码见这里,也可以直接看书中提供的地址。
总结
读这本书的过程非常让人过瘾,不时也有恍然大悟,虽然深度一般,但是对于入门书来说非常的合适,因此特写这篇总结来推荐给大家,所有算法工程师以及工程师都可以找来看看。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号