Pytorch04_RNN结构
RNN结构
本文中的RNN泛指LSTM,GRU等等
CNN中和RNN中batchSize的默认位置是不同的。
CNN中:batchsize 的位置是 position 0.
RNN中:batchsize 的位置是 position 1.
一、pytorch中两种调取方式
对于最简单的RNN,我们可以使用两种方式来调用.
torch.nn.RNNCell() 它只接受序列中的单步输入,必须显式的传入隐藏状态。torch.nn.RNN() 可以接受一个序列的输入,默认会传入一个全0的隐藏状态,也可以自己申明隐藏状态传入。
RNN结构及隐藏状态是什么参考下文 https://www.cnblogs.com/Haozi-D17/p/13264745.html
二、参数及输入输出结构
输入大小
输入大小是三维tensor[seq_len,batch_size,input_dim]
input_dim 是输入的维度 或者说是 数据的特征数,比如是128
batch_size 是一次往RNN输入句子的数目 或者说是 有几组独立的输入数据,比如是5。
seq_len 是一个句子的最大长度 或者说是 每组训练数据的时间长度,比如15
输入顺序
注意,RNN输入的是序列,一次把批次的所有句子都输入了,得到的 ouptut 和 hidden 都是这个批次的所有的输出和隐藏状态,维度也是三维。
可以理解为现在一共有 batch_size 个独立的 RNN 组件,RNN的输入维度是 input_dim,总共输入 seq_len 个时间步,则每个时间步输入到这个整个RNN模块的维度是 [batch_size,input_dim]
将 seq_len 放在第一位的好处是,可以同时处理每个句子
1. 第一个时间步,输入所有句子的第一个单词 或者 第一个时间上的所有特征;
2. 第二个时间步,输入所有句子的第二个单词 或者 第二个时间上的所有特征;
...
3. 以此类推,直到 seq_len 个时间步全部输入完成。
举例
# 构造RNN网络,x的维度5,隐层的维度10,网络的层数2
rnn_seq = nn.RNN(5, 10,2)
# 构造一个输入序列,句长为 6,batch 是 3, 每个单词使用长度是 5的向量表示
x = torch.randn(6, 3, 5)
#out,ht = rnn_seq(x,h0)
out,ht = rnn_seq(x) #h0可以指定或者不指定
问题1:这里 out、ht 的 size 是多少呢?
回答:out: 6 * 3 * 10, ht: 2 * 3 * 10,out 的输出维度 [seq_len,batch_size,output_dim],ht 的维度 [num_layers * num_directions, batch_size, hidden_size], 如果是单向单层的 RNN 那么一个句子只有一个 hidden。
问题2:out[-1] 和 ht[-1] 是否相等?
回答:相等,隐藏单元就是输出的最后一个单元,可以想象,每个的输出其实就是那个时间步的隐藏单元
可以想象 当 input 为 [seq_len,batch_size,input_dim] 时:
out 的 维度 即为 将输入每个时间步上的 特征做了映射,因此只改变最后一个维度,得到的结果即为 [seq_len, batch_size, output_dim]
ht 的 第一个维度 与句子长度无关,因为只是在不断改变和更新的过程,但方向和层数 会影响,为num_layers * num_directions。
第二个维度为batch_size,有几个句子就得到几个维度。
最后一个维度同 out 的维度变换,为 hidden_size
ht 的维度 [num_layers * num_directions, batch_size, hidden_size]
但 out[-1] = ht[-1](上述代码中),是因为 ht 最终 只保存最后一个时刻的值
RNN的其他参数
nn.RNN(input_dim ,hidden_dim ,num_layers ,…)
– input_dim 表示输入的特征维度
– hidden_dim 表示输出的特征维度,如果没有特殊变化,相当于out
– num_layers 表示网络的层数
– nonlinearity 表示选用的非线性**函数,默认是 ‘tanh’
– bias 表示是否使用偏置,默认使用
– batch_first 表示输入数据的形式,默认是 False,就是这样形式,(seq, batch, feature),也就是将序列长度放在第一位,batch 放在第二位
– dropout 表示是否在输出层应用 dropout
– bidirectional 表示是否使用双向的 rnn,默认是 False
LSTM
LSTM的输出相比于GRU多了一个memory单元
# 输入维度 50,隐层100维,两层
lstm_seq = nn.LSTM(50, 100, num_layers=2)
# 输入序列seq= 10,batch =3,输入维度=50
lstm_input = torch.randn(10, 3, 50)
out, (h, c) = lstm_seq(lstm_input) # 使用默认的全 0 隐藏状态
问题1:out和(h,c)的size各是多少?
回答:out:(10 * 3 * 100),(h,c):都是(2 * 3 * 100)
问题2:out[-1,:,:]和h[-1,:,:]相等吗?
回答: 相等
GRU比较像传统的RNN
gru_seq = nn.GRU(10, 20,2) # x_dim,h_dim,layer_num gru_input = torch.randn(3, 32, 10) # seq,batch,x_dim out, h = gru_seq(gru_input)
三、代码案例
以一个时间序列预测为例。代码以先后顺序写,直接按顺序复制即可运行。
首先,导入库
import numpy as np import pandas as pd import matplotlib.pyplot as plt import torch
演示一下我们需要做的事,这部分不用再自己的代码中跑,单纯演示
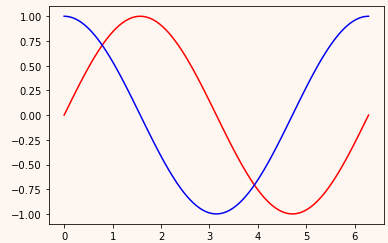
steps = np.linspace(0, np.pi*2, 100, dtype=np.float32) x = np.sin(steps) y = np.cos(steps) plt.plot(steps, x, "r-") plt.plot(steps, y, "b-") plt.show()
如下图,输入为红色的线上的点,想要输出为对应的蓝色的点,即用 sin上的点 预测 同样位置的 cos 上的点
生成所用数据 x 和 y
train_x = np.zeros(shape=(100, 10, 1)) train_y = np.zeros(shape=(100, 10)) for step in range(100): start, end = step * np.pi, (step+1)*np.pi steps = np.linspace(start, end, 10, dtype=np.float32) train_x[step,:,0] = np.sin(steps) # float32 for converting torch FloatTensor train_y[step,:] = np.cos(steps)
# 转换为张量
train_x = torch.from_numpy(train_x)
train_y = torch.from_numpy(train_y)
train_x 为 一条 sin 曲线,shape 为 (100, 10, 1)train_y 为 一条 cos 曲线,shape 为 (100, 10)
将 x 和 y 打包为数据集
其中:
32 表示从中取数据的时候每次取出32组(一共有100组)
shuffle=True 表示取数据的时候 将100组数据打乱,随机取
num_workers = 2 表示使用多线程
import torch.utils.data as Data torch_dataset = Data.TensorDataset(train_x, train_y) loader = Data.DataLoader( dataset=torch_dataset, batch_size=32, shuffle=True, # 每次训练打乱数据, 默认为False num_workers=2, # 使用多进行程读取数据, 默认0,为不使用多进程 )
构建 GRU 模型
import torch.nn as nn import torch.optim as optim # 搭建模型 input_size = 1 hidden_size = 16 output_size = 10 num_layers = 1 class GRU(nn.Module): def __init__(self, ): super(GRU, self).__init__() self.gru = nn.GRU(input_size=input_size, # feature_len=1 hidden_size=hidden_size, # 隐藏记忆单元尺寸hidden_len num_layers=num_layers, #层数 batch_first=True, # 在传入数据时,按照[batch,seq_len,feature_len]的格式 ) self.linear = nn.Linear(hidden_size, output_size) #输出层 def forward(self, x): out, h_t = self.gru(x) # out(batch, seq_len, feature_len) # 思路一:将out的所有结果 都输到 linear,再取最后一个 # 因为要将out输入linear,因此先将batch和time_step打平 # out = out.reshape(-1, hidden_size) # [batch,seq_len,hidden_len]->[batch*seq_len,hidden_len] # out = self.linear(out) # [batch*seq_len,hidden_len] # out = out.unsqueeze(dim=0) # 增加一个维度batch [seq_len,feature_len]->[batch=1,seq_len,feature_len] # out = out.reshape(-1, 10, output_size) # 重新恢复为原来的维度(最后一个维度变了) # out = out[:, -1, :] # 只取最后一个 取出的out.shape为 torch.Size([batch, output_size]) # 思路二:直接取out的最后一个时间维度的结果输入到 linear out = out[:, -1, :] out = self.linear(out) return out
batch_first=True,如开头所说,默认的输入应该为 [seq_len, batch, feature_len], 此参数设为True,表示输入为[batch,seq_len, feature_len]
设置优化器和损失计算函数
model = GRU().cuda() # 若不用GPU 删掉.cuda()即可 criterion = nn.MSELoss() optimizer = optim.Adam(model.parameters(), lr=1e-2)
训练
for epoch in range(100): for step, (batch_x, batch_y) in enumerate(loader): x = batch_x.float().cuda() y = batch_y.float().cuda() # .reshape(-1, 1, Out).cuda() output = model(x) loss = criterion(output, y).cuda() model.zero_grad() loss.backward(retain_graph=True) # optimizer.step() if epoch: # % 100 == 0: print("Epoch: ", epoch, "| Loss: ", loss.item()) # 展示结果的地方解释这段 # pre = model(train_x.float().cuda()) # plt.plot(pre[0,:].cpu().detach().numpy(), c="r") # plt.plot(train_y[0,:], c="b") # plt.show()
将训练用的 x 重新输入得到预测结果
pre = model(train_x.float().cuda()) print(pre)
效果展示
任意比较一组预测值与实际值,若想比较所有的值,将预测的100组连起来就好了。
上面预测的数据在GPU上存着,画图需要在cpu上复制一份数据,并转换为numpy 才能在cpu上画图
plt.plot(pre[0,:].cpu().detach().numpy(), c="r") plt.plot(train_y[0,:], c="b")
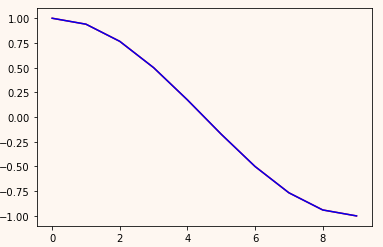
可以看出,基本重合
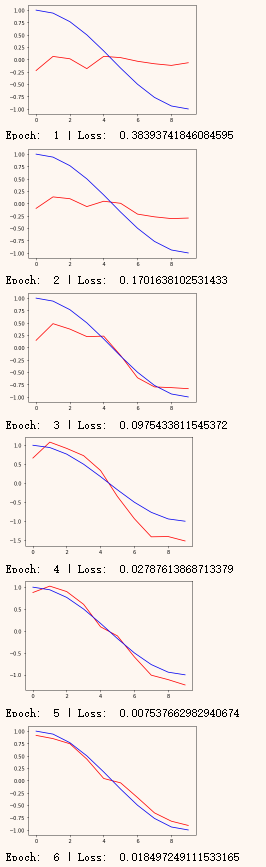
下图表示动态变化,可以看出没用几次就可以训练的很好了。
就是训练的代码框里最后注释掉的一段,如果不注释就会看到训练的效果(方法比较简单,有更好的方法,可以自己搜一下)