相当于是树上的一个trick。

1. 算法简介

类似于重链剖分，我们根据子树深度最深的节点建立重儿子，我们可以得到以下性质。

• 所有链长之和为 $n$。
• 任意一个节点的 $k$ 级祖先所在长链的长度大于 $k$。
• 任意叶子节点向上最多经过 $\sqrt{n}$ 个轻边。
  • 证明：经过一个轻边，则跳到的长链长度一定大于当前长链的长度，则最坏情况为 $1+2+...\sqrt{n}$，即 $\sqrt{n}$ 次跳跃，稍劣于重链剖分的 $\log n$。

2. 基础应用

2.1 树上 K 级祖先

长链剖分可以在线 $O(n\log n)-O(1)$，求出 $x$ 节点的 $k$ 级祖先。

我们首先倍增预处理出每个节点 $x$ 的 $2^k$ 级祖先 ，复杂度 $O(nlogn)$，然后对于每一条长链，我们都从链顶向上/向下存储走 $d$ 步所到的节点，$d$ 不大于长链深度，复杂度 $O(n)$。

对于每一个询问 $(x,k)$，我们首先跳到 $x$ 的 $2^{h_k}$ 级祖先，其中 $h_k$ 为 $k$ 的二进制最高位，即 $\lfloor {\log }_{2}k\rfloor$，然后我们跳到该长链链顶，根据步数容易查询答案，复杂度 $O(1)$。

模板:树上 K 级祖先

int n,m,rt;
ui s;
struct edge{
	int ver,nx;
}e[N<<1];
int hd[N],tot;
void link(int x,int y){e[++tot] = {y,hd[x]},hd[x] = tot;}


int f[N][22],g[N];
struct tree{
	int dep[N],son[N],d[N],top[N];
	vector<int>up[N],down[N];
	void dfs1(int x){
		for(int i = 1;i <= 20;i++)f[x][i] = f[f[x][i-1]][i-1];//倍增预处理
		for(int i = hd[x];i;i = e[i].nx){
			int y = e[i].ver;
			dep[y] = d[y] = dep[x] + 1,f[y][0] = x;
			dfs1(y);
			d[x] = max(d[x],d[y]);
			if(!son[x] || d[y] > d[son[x]])son[x] = y;
		} 
	}//长剖 
	void dfs2(int x,int t){
		top[x] = t;
		if(x == t){
			for(int i = 0,now = x;i <= d[x] - dep[x];i++)up[x].push_back(now),now = f[now][0];
			for(int i = 0,now = x;i <= d[x] - dep[x];i++)down[x].push_back(now),now = son[now]; 
		}//预处理链顶节点的子孙父亲 
		if(!son[x])return;
		dfs2(son[x],t);
		for(int i = hd[x];i;i = e[i].nx){
			int y = e[i].ver;
			if(y != son[x])dfs2(y,y);
		}
	}
	void build(){dep[rt] = 1,dfs1(rt),dfs2(rt,rt);}
	int ask(int x,int k){
		if(!k)return x;
		x = f[x][g[k]],k -= (1ll << g[k]);
		k -= (dep[x] - dep[top[x]]),x = top[x];
		return k > 0 ? up[x][k] : down[x][-k];
	}
}t;


inline ui get(ui x) {
	return x ^= x << 13, x ^= x >> 17, x ^= x << 5, s = x; 
}

int main(){
	n = read(),m = read(),s = read();g[0] = -1;
	for(int i = 1;i <= n;i++)g[i] = g[i>>1] + 1;//highbit
	for(int i = 1;i <= n;i++){
		int x = read();
		if(!x)rt = i;
		else link(x,i);
	}
	t.build();
	int las = 0;
	ll ans = 0;
	for(int i = 1;i <= m;i++){
		int x = (get(s) ^ las) % n + 1;
		int k = (get(s) ^ las) % t.dep[x];
		las = t.ask(x,k);
		ans ^= (ll)i * las;
	} 
	printf("%lld\n",ans);

    return ,0;
}

2.2 例题

I CF208E Blood Cousins
即求 $x$ 的 $k$ 级祖先的深度为 $k$ 的儿子的数量。

首先第一步可以用上述方法 $O(n\log n)-O(1)$ 求，第二步即求 $x$ 节点深度为 $k$ 的儿子数量，可以 离线 + 长链剖分优化 DP（详见第 3 部分），复杂度 $O(n)$。

还有一种 dsu on tree $O(n\log n)$ 的方法。

代码

II P5384 [Cnoi2019] 雪松果树
上一题的加强版，只是将 ${10}^5$ 加强成了 ${10}^6$，上一题的代码交上去 96 tps，卡一卡可能能过 : )，不过我不会。

首先我们第二步是 $O(n)$ 的，不需要优化，我们考虑优化第一步，我们离线考虑，dfs 一遍即可，复杂度 $O(n)$。

具体的：我们开一个栈，遍历它们的 dfs 序，对于每一个节点，我们只需要在栈内向前找 $k$ 个即可找到 $k$ 级祖先，因为栈内只有该节点的祖先。

总复杂度 $O(n)$。

代码 甚至比上一题短 : (

3. 长链剖分优化dp

3.1 引入

重点!!

长链剖分可以优化树上 与深度相关 的 DP。一般有 $f_{i,j}$ 表示 以 $i$ 为根的子树中，深度为 $j$ 的贡献。

可以将该 DP 优化到 $O(n)$。

例题：CF1009F Dominant Indices

以该题来引入，我们设 $f_{i,j}$ 为以 $i$ 为根的子树内深度为 $j$ 的节点个数，则有转移方程:

直接写是 $O(n^2)$ 的，考虑优化，对于每个节点 $x$，对于它的重儿子，我们直接继承它的答案，然后暴力的合并轻儿子。这样做，每一个节点最多在链顶合并一次，且合并复杂度为链长，总合为 $O(n)$，十分优秀。

3.2 细节与实现

有用 vector 与 指针 的两种方法，这里介绍指针方法，实现更简单（当然因为是指针可能会有玄学错误 : ( ），常数更小。

我们利用指针动态申请内存，对于一条长链，其共用一个大小为其长度的数组，这样只需要在继承重儿子时根据 DP 简单转移即可。

3.3 例题

I CF1009F Dominant Indices

长链剖分例题，指针实现代码。

II COGS 2652. 秘术「天文密葬法」

(不会 01分数规划 的可以看我的笔记 - 01分数规划小记)
首先有分数规划，我们二分一个 $mid$，则令每个点的权值为 $a_i-mid\times b_i$ ，转化为判断树上是否存在一条长为 $m$ 的路径使得路径上权值和小于等于零，显然可以淀粉质，是 $O(n{\log }^{2}n)$ 的，这里不做讨论。

我们考虑 DP，设 $f_{i,j}$ 表示 $i$ 节点开始向下走 $j$ 步的最小权值和，则显然有转移：

直接写是 $O(n^2)$ 的，由于只与深度相关，我们考虑长链剖分优化，由于转移中有 权值，我们可以做类似 树上差分 的操作，可以 $O(1)$ 把权值求出，然后我们找出权值和最小长度为 $m$ 的路径，进而二分即可。

复杂度 $O(n\log V)$。

代码

III P3899 [湖南集训] 更为厉害
首先对于每一个询问 $(p,k)$，我们分类讨论 $b$ 的位置。

• $b$ 是 $p$ 的祖先，这样 $c$ 可以取到 $p$ 的所有子节点，答案为 $min(de{p}_p-1,k)\times (siz{e}_p-1)$。
• $b$ 在 $p$ 的子树内，对于子树内与 $p$ 距离不超过 $k$ 的节点 $b$，$c$ 可以取到 $b$ 的所有子节点，我们要求所有满足条件的 $b$ 的 $siz{e}_b-1$ 的和。

我们写出式子，其实是二位偏序的类型，可以简单做到 $O(q\log n)$，这里不做讨论。

我们考虑 DP，设 $f_{x,j}=\sum _{y\in T(x),y\ne x}[dis(x,y)\le j]siz{e}_y-1$ (注意没有 $x$ 节点)，则有转移方程:

我们 离线询问，长链剖分优化，我们需要一个标记数组方便我们查询，类似上一题 差分。

复杂度 $O(n+q)$，注意 long long
代码

IV P5904 [POI2014] HOT-Hotels 加强版
极好的题，让我的脑袋旋转。

首先我们考虑 DP，令 $f_{i,j}$ 表示以 $i$ 为根，深度为 $j$ 的节点个数，$g_{i,j}$ 表示当前已经加入子树中满足深度为 $j$，且不在同一棵子树的点对 $(x,y)$ 的方案数，我们考虑在三点的中点统计，这样可以 $O(n^2)$ 做出简单版。

我们考虑如何优化，首先我们固定根为 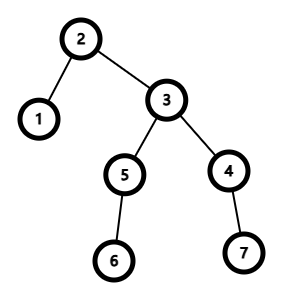$1$，这样的话若依旧按上述方法会不好考虑一种情况:
显然有 $(1,6,7)$ 一组，但是我们不好在 $3$ 处统计，我们考虑改变状态使得可以在 $2$ 处统计此种答案，我们设 $g_{i,j}$ 表示在以 $i$ 为根的子树内，点对 $(x,y)$，使得 $d(x,lca(x,y))=d(y,lca(x,y))=d(i,lca(x,y))+j$ 的方案数，即我们还需要长为 $j$ 的链即可得到一种方案，例如上图我们在 $2$ 处只需要一个长为 $1$ 的链即可产生贡献，这样是好统计的，状态转移不太好想。

我们仅考虑只合并该子树 $y$ 的贡献，得：

• $g_{x,j}\leftarrow g_{y,j+1}$，儿子需要 $j+1$ 长的链，则自己只需要长度为 $j$ 的链。
• $g_{x,j}\leftarrow f_{x,j}\times f_{y,j-1}$，两个长为 $j$ 的链还需要一个长为 $j$ 的链。

对这些式子长链剖分优化即可。

我们观察 $g$ 可以发现此状态是倒叙转移的，在通过长链剖分优化时需要注意指针的运用，因为一些玄学问题，我的代码只能让两个数组公用一个内存，而且需要开双倍内存，如有知道问题可以敲敲我 : )，Orz。

复杂度 $O(n)$。

代码

V P4292 [WC2010] 重建计划
没上一题难

其实就是 II 的加强版，分数规划，二分一个 $mid$，使权值变为 $v_i-mid$，我们要判断是否有长度在 $[L,U]$ 的路径的权值和 大于等于 零，和 II 一样的 DP 状态与转移，设 $f_{i,j}$ 表示 $i$ 节点开始向下走 $j$ 步的最大权值和，则有转移：

有边权转点权的操作。
加一个标记数组，类似 树上差分，或者也可以暴写区间修改线段树 : (，然后我们建立个线段树，存 DP 中区间最大值，我们可以按照 $dfs$ 序存储，在统计答案时，只需找链长在区间内权值和最大的即可。

复杂度 $O(n{\log }^{2}n)$。

本题还有神神淀粉质做法，有兴趣可以了解: (

代码

4. 基于长链剖分的贪心

一个经典结论：选一个节点能覆盖它到根的所有节点。选 $k$ 个节点，覆盖的最多节点数就是前 $k$ 条长链长度之和，选择的节点即 $k$ 条长链末端.

参考文章：

长链剖分总结 - 租酥雨
简单树论 - Alex_wei
长链剖分学习笔记 - Ynoi