多项式整合包

update:

学习多项式!!

1.快速傅里叶变换(FFT)

当然是从 \(FFT\) 开始了:)

1.1 DFT & IDFT

1.1.1 系数与点值

系数表达: \(F(x) = \sum_{i=0}^n F[i]x^i\)

\(F[i]\) 叫做多项式 \(F(x)\) 的 系数。
这样我们求 \(C(x) = F(x) \ast G(x)\) 的系数:

\[C[k] = \sum_{i=0}^k F[i]G[k-i] \]

直接算的复杂度显然是 \(O(n^2)\) 的。

然后我们要知道: n+1个点值(有序数对)可以来确定一个n次多项式 \(F(x)\) (具体的可以看 拉格朗日插值) 。
所以多项式的 点值表达 就是用 \(n+1\) 的 点值 来表示多项式。
点值表达： $ F(x) = (x_0,y_0),(x_1,y_1),...,(x_n,y_n) $ 。

我们利用这样的表示法可以快速的求出两个 多项式的乘法。
只需将 \(F(x)\) 与 \(G(x)\) 的 点值对应值直接乘 即可。

但是 \(F(x) \ast G(x)\) 明明有 \(2n\) 项，怎么办。

我们直接找 \(2n+1\) 个点就可以了。

这样我们就完成了 \(F(x) \ast G(x)\) 的点值表达:\((x_0,F_{x_0} \ast G_{x_0}),(x_1,F_{x_1} \ast G_{x_1}),...,(x_{2n},F_{x_{2n}} \ast G_{x_{2n}})\) 。
复杂度仅需 \(O(2n)\) 。

1.1.2 FFT的流程

上述我们可以知道在多项式乘法中 点值表达 的复杂度很优，但是我们一般的多项式都是系数表达 ，我们如何实现 点值 与 系数 之间的转换呢？: )

“把系数表达转换为点值表达”的算法叫做 DFT

“把点值表达转换为系数表达”的算法叫做 IDFT(DFT的逆运算)

传承老图：

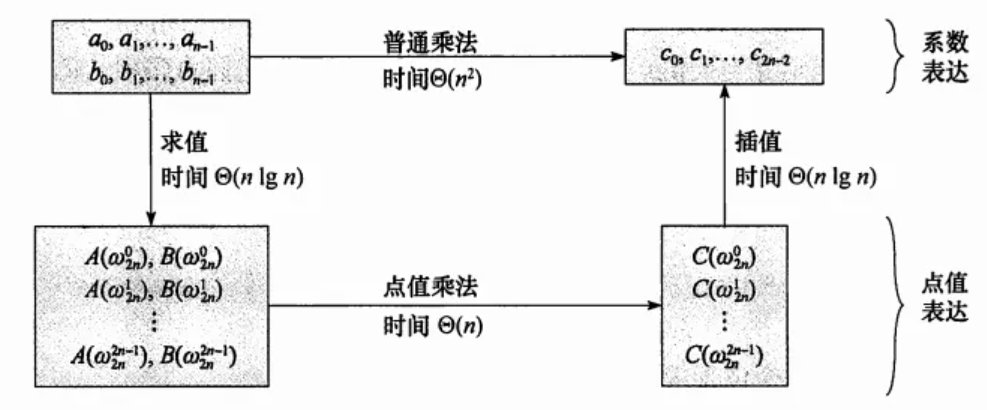
• 从一个多项式的系数表达确定其点值表达的过程称为求值
• 而求值运算的逆运算(也就是从一个多项式的点值表达确定其系数表达)被称为插值.

1.2 单位根的性质

这一点讲如何利用一些有神奇性质的 \(x\) 。

复数 不讲。

n次单位根： 方程 \(x^n = 1\) 的 \(n\) 个解。
几何意义：将单位圆均分为 \(n\) 份，我们将幅角为 \(\frac k n\) 长度为 \(1\) 的根称为 \(\omega^k_n\)
复数表示： \(\omega^k_n = cos\frac{2kπ}{n} + sin\frac{2kπ}{n}i\)

单位根的性质：

• \(\omega^j_n * \omega^i_n = \omega^{i+j}_n\)
• \(\omega^{2k}_{2n} = \omega^k_n\)，根据几何或者直接表示为复数易证。
• \(\omega^{k+n}_n = \omega^k_n\)，几何上相当于绕了一个圆周
• \(\omega^{k+\frac n 2}_n = \omega^{k+\frac n 2}_n = \omega^k_n * \omega^{\frac n 2}_n = -\omega^k_n\)，几何上相当于转了半个圆周

这些性质有大用

1.3 单位根的巧用

一个多项式 \(F(x) = \sum_{i=0}^{n} F[i]x^i\)。
我们把它拆成平均的两份：

\[\large F^0(x) = F[0] + F[2]x + ... + F[n-1]x^{\frac n {2}-1} \]

\[\large F^1(x) = F[1] + F[3]x + ... + F[n]x^{\frac n {2}-1} \]

则可以得到 \(F(x) = F^0(x^2) + xF^1(x^2)\)
这样就可以分治了！！
我们把神奇的单位根带入进去：

• \(1. k > \frac n 2\) 代入 \(\omega^k_n\)
  \(F(\omega^k_n) = F^0((\omega^k_n)^2) + \omega^k_n F^1((\omega^k_n)^2) = F^0(\omega^k_{\frac n 2}) + \omega^k_n F^1(\omega^k_{\frac n 2})\)
• \(2. k < \frac n 2\) 代入 \(\omega^{k+\frac n 2}_n\)
  \(F(\omega^{k+\frac n 2}_n) = F^0((\omega^{k+\frac n 2}_n)^2) + \omega^{k+\frac n 2}_n F^1((\omega^{k+\frac n 2}_n)^2) = F^0(\omega^k_{\frac n 2}) - \omega^k_n F^1(\omega^k_{\frac n 2})\)

两式的差别只是正负号。

有什么用呢？可以快速求值，我们利用 \(1\) 式可以用 \(F^0(x)\) 与 \(F^1(x) O(n)\) 求出 \(\omega^0_n,\omega^1_n,...,\omega^{\frac n 2-1}_n\) 的点值，类似利用 \(2\) 式的可以求出 \(\omega^{\frac n 2}_n,...,\omega^{n-1}_n\) 的点值。

最终得出来了 \(F(x)\) 的点值！这是一个分治过程，即可以 \(O(nlogn)\) 的复杂度完成 求值 (即DFT)

至于IDFT。
结论：只需带入 \(\omega^{-k}_n\) 最后除 \(n\) 即可，证明先咕。

1.4 FFT 的实现

上面听不懂没关系，背代码就行了:(

我们上面的方法是递归分治的，会造成大量数组拷贝，是不优的。
有一种方法可以避免，就是迭代FFT(即从小合并)。
但这样我们需要找出每个点最后所在的位置，结论就是原数字的二进制翻转(很奇怪)，可以 \(O(n)\) 求。

for(int i = 1;i < k;i++)rev[i] = (rev[i>>1]>>1) | ((i&1)<<(b-1));

剩下的直接看代码吧:)

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define db double
const int N = 2e6+1e5;//2^20 = 1048576
const db pi = acos(-1.0);

inline int read(){
    int x = 0,f = 1;char c = getchar();
    for(;c < '0' || c > '9';c = getchar())if(c == '-')f = -1;
    for(;c >= '0' && c <= '9';c = getchar())x = (x<<1) + (x<<3) + c-'0';
    return x * f;
}

struct cp{
    db x,y;
    cp(){x = y = 0;}
    cp(db x,db y):x(x),y(y){}
    inline cp operator + (const cp a)const{return cp(a.x+x,a.y+y);}
    inline cp operator - (const cp a)const{return cp(x-a.x,y-a.y);}
    inline cp operator * (const cp a)const{return cp(x*a.x-y*a.y,x*a.y+y*a.x);}
}F[N],G[N];

int n,m;
int rev[N],b;

void FFT(int n,cp *a,int op){
    for(int i = 0;i < n;i++)if(i < rev[i])swap(a[i],a[rev[i]]);
    for(int len = 1;len <= (n>>1);len <<= 1){
        cp w1(cos(pi/len),sin(pi/len)*op);
        for(int i = 0;i <= n - (len<<1);i += (len<<1)){
            cp w(1,0);
            for(int j = i;j < i+len;j++){
                cp x = a[j],y = w*a[j+len];
                a[j] = x+y,a[j+len] = x-y;
                w = w * w1;
            }
        }
    }
}
int main(){
    n = read(),m = read();
    for(int i = 0;i <= n;i++)F[i].x = read();
    for(int i = 0;i <= m;i++)G[i].x = read();
    int k = 1;
    while(k <= n+m)k <<= 1,b++;
    for(int i = 1;i < k;i++)rev[i] = (rev[i>>1]>>1) | ((i&1)<<(b-1));
    FFT(k,F,1),FFT(k,G,1);
    for(int i = 0;i <= k;i++)F[i] = F[i] * G[i];
    FFT(k,F,-1);
    for(int i = 0;i <= n+m;i++)printf("%d ",(int)(F[i].x/k+0.5));

	return 0;

}

全文背默！！！

1.5 其他优化

咕咕咕

1.6 快速数论变换(NTT)

学原根回来哩:)
因为FFT引用了复数单位根，所以精度要求很高，跑的可能会慢。
所以我们需要NTT。

1.6.1 阶与原根

详见数论学习笔记1.3
我就不搬了。

1.6.2 原根类似的性质

(以下 \(g\) 代表模 \(p\) 的最小原根)
由原根性质2可得 \(g^1,g^2,...,g^{\varphi(p)}\) 模 \(p\) 两两不同余。

我们令 \(\omega_n = g^{\frac {p-1} n}\)，你问不整除怎么办，我们就找能整除的 \(p\)。

所以我们有以下性质：

• \(\omega_n^n = (g^{\frac {p-1} n})^n = g^{p-1} \equiv 1\pmod p\)
• \(\omega_{2n}^{2k} = (g^{\frac {p-1} {2n}})^{2k} = (g^{\frac {p-1} n})^k = \omega_n^k\)
• \(\omega_{n}^{k+n} = (g^{\frac {p-1} n})^{k+n} \equiv (g^{\frac {p-1} n})^k = \omega_n^k\pmod p\)
• \(\omega_{n}^{k+\frac n 2} = (g^{\frac {p-1} n})^{k+\frac n 2} \equiv -(g^{\frac {p-1} n})^k = -\omega_n^k\pmod p\)

第四条证明一下：

• 由费马小定理知 \(g^{p-1} - 1\equiv 0\pmod p\)，即 \((g^{\frac {p-1} 2} - 1)(g^{\frac {p-1} 2} + 1) \equiv 0 \pmod p\)，即 \(g^{\frac {p-1} 2} \equiv \pm 1\)，又因为 \(g^i\) 互不相同且 \(g^{\varphi(p)} \equiv 1\pmod p\)，得出 \(g^{\frac {p-1} 2} \equiv -1\pmod p\)，即得证。

这样原根与单位根的性质就完全相同了！！: )

我们只需要找到一个模数 \(p\) 使得任意 \(n\) 都整除 \(p-1\) 即可，而一般 \(n\) 都是 \(2\) 的次幂。

一般NTT模数：
\(998244353 = 119 * 2 ^ {23} + 1\)，\(g\) 为 \(3\)。
\(1004535809 = 479 * 2 ^ {21} + 1\)，\(g\) 为 \(3\)。

大佬的NTT模数表

模版

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define F(i,a,b) for(int i = a;i <= b;i++)
#define D(i,a,b) for(int i = a;i >= b;i--)
#define in inline
#define pb(x) push_back(x)
#define db double  
const db pi = acos(-1);
const int N = 2e6+1e5,mod = 998244353,g = 3;

ll read(){
    ll x = 0,f = 1;char c = getchar();
    for(;c < '0' || c > '9';c = getchar())if(c == '-')f = -1;
    for(;c >= '0' && c <= '9';c = getchar())x = (x<<3) + (x<<1) + c-'0';
    return x * f;
}

int ksm(int x,int y = mod-2){
    int ans = 1;
    while(y){
        if(y & 1)ans = 1ll * ans * x % mod;
        x = 1ll * x * x % mod,y >>= 1;
    }return ans;
}


int b,n,m;
int rev[N],invg = ksm(g),invn;
ll F[N],G[N];

void NTT(int n,ll *a,int op){
    F(i,0,n)if(i < rev[i])swap(a[i],a[rev[i]]);
    for(int len = 1;len <= (n>>1);len <<= 1){
        ll tg = ksm(op?g:invg,(mod-1)/(len<<1));
        for(int i = 0;i + (len<<1) <= n;i += (len<<1)){
            ll gg = 1;
            for(int j = i;j < i + len;j++){
                ll x = a[j],y = 1ll * gg * a[j+len] % mod;
                a[j] = (x + y) % mod,a[j+len] = (x - y + mod) % mod;
                gg = 1ll * gg * tg % mod;
            }
        }
    }
}
int main(){
    n = read(),m = read();
    F(i,0,n)F[i] = read();
    F(i,0,m)G[i] = read();
    int t = 1;
    while(t <= n+m)t <<= 1,b++;
    F(i,1,t)rev[i] = ((rev[i>>1]>>1) | (i&1)<<(b-1));
    NTT(t,F,1),NTT(t,G,1);
    F(i,0,t)F[i] = F[i] * G[i] % mod;
    NTT(t,F,0);invn = ksm(t);
    F(i,0,n+m)printf("%d ",int(F[i] * invn % mod));
    printf("\n");
    

    return cerr<<endl<<"Time:"<<clock()<<"ms"<<endl,0;

}

2. 多项式求逆

咕咕咕

参考资料：
快速傅里叶变换|快速数论变换