【学习笔记】深度学习 demo2 二次函数回归

在本demo中，我们使用的二次函数为

$$\begin{aligned} f(x) &= \left(x - 4 \right) \left(x - 8\right) + rand \\ &= x ^ 2 - 12 x + 32 + rand \end{aligned}$$

其中$rand$表示一个满足标准正态分布$N\left(0, 1\right)$的随机数（平均值为0，方差为1）

基于Parameter手动构建

我们可以尝试用类似的方式，从参数（Parameter）开始构建一个二次函数。

一个二次函数的基本结构如下

$$g\left(x\right)=ax^2+bx+c$$

其中包含三个参数：$a$、$b$、$c$。

代码如下：

import matplotlib.pyplot as plt
import torch
from torch import nn
from torch.autograd import Variable


class SquareRegression(nn.Module):
    def __init__(self):
        nn.Module.__init__(self)
        self.a = nn.Parameter(torch.randn(1, 1), requires_grad=True)  # 1 x 1
        self.b = nn.Parameter(torch.randn(1, 1), requires_grad=True)  # 1 x 1
        self.c = nn.Parameter(torch.randn(1, 1), requires_grad=True)  # 1 x 1

    def forward(self, x_):
        p_ = (x_ ** 2).mm(self.a)  # n x 1
        q_ = x_.mm(self.b)         # n x 1
        t_ = self.c                # 1 x 1
        return p_ + q_ + t_.expand_as(p_)  # n x 1


if __name__ == "__main__":
    n = 100
    x = torch.linspace(-2, 12, n).resize_((n, 1))  # n x 1 tensor
    y = (x - 4) * (x - 8) + torch.randn(x.size())  # n x 1 tensor

    model = SquareRegression()

    criterion = nn.MSELoss()
    optimizer = torch.optim.SGD(model.parameters(), lr=2e-5)

    num_epochs = 500000
    for epoch in range(num_epochs):
        inputs, targets = Variable(x), Variable(y)

        out = model(inputs)
        loss = criterion(out, targets)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if (epoch + 1) % 100 == 0:
            print('Epoch[{}/{}], loss:{:.6f}'.format(epoch + 1, num_epochs, loss.item()))

    for name, param in model.named_parameters():
        print(name, param.data)

    predict = model(x)

    plt.plot(x.numpy(), y.numpy(), 'ro', label='Original Data')
    plt.plot(x.numpy(), predict.data.numpy(), label='Fitting Line')
    plt.show()

输出结果如下：

Epoch[100/500000], loss:386.833191
Epoch[200/500000], loss:385.401001
Epoch[300/500000], loss:383.982391
Epoch[400/500000], loss:382.576904
Epoch[500/500000], loss:381.184418
Epoch[600/500000], loss:379.804657
Epoch[700/500000], loss:378.437256
Epoch[800/500000], loss:377.082153
Epoch[900/500000], loss:375.738983
Epoch[1000/500000], loss:374.407532
Epoch[1100/500000], loss:373.087585
Epoch[1200/500000], loss:371.778870
Epoch[1300/500000], loss:370.481293
Epoch[1400/500000], loss:369.194580
Epoch[1500/500000], loss:367.918549

... ... ... ...

Epoch[499400/500000], loss:0.985296
Epoch[499500/500000], loss:0.985296
Epoch[499600/500000], loss:0.985296
Epoch[499700/500000], loss:0.985296
Epoch[499800/500000], loss:0.985296
Epoch[499900/500000], loss:0.985296
Epoch[500000/500000], loss:0.985296
a tensor([[1.0048]])
b tensor([[-12.0305]])
c tensor([[31.8826]])

生成图像如下：

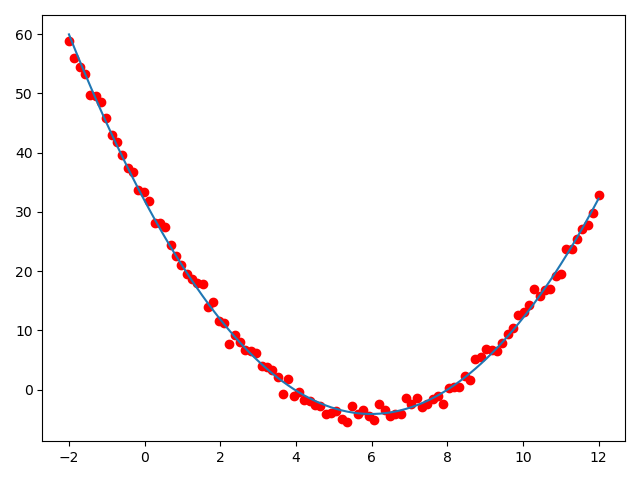
可以发现，我们生成的拟合解如下

$$\begin{cases} a &= 1.0048 \\ b &= -12.0305 \\ c &= 31.8826 \end{cases}$$

所得到的函数为

$$\begin{aligned} g\left(x\right) &= a x^2 + b x + c \\ &= 1.0048 x^2 -12.0305 x + 31.8826 \end{aligned}$$

和原公式$f(x) = x^2 - 12 x + 32$已经十分接近，图像上的拟合结果也与期望结果基本一致。

基于Linear叠加构建

除此之外，我们还可以通过叠加Linear来构建一个二次函数。

本次使用的公式如下：

$$\begin{aligned} h\left(x\right) &= \left(w_1 x + b_1\right) \left(w_2 x + b_2\right) \\ &= w_1 w_2 x + \left(w_1 b_2 + w_2 b_1\right)x + b_1 b_2 \end{aligned}$$

包含四个参数$w_1$、$b_1$、$w_2$、$b_2$。

代码如下：

import matplotlib.pyplot as plt
import torch
from torch import nn
from torch.autograd import Variable


class SquareRegression(nn.Module):
    def __init__(self):
        nn.Module.__init__(self)
        self.linear1 = nn.Linear(1, 1)
        self.linear2 = nn.Linear(1, 1)

    def forward(self, x_):
        return self.linear2(x_) * self.linear1(x_)  # n x 1


if __name__ == "__main__":
    n = 100
    x = torch.linspace(-2, 12, n).resize_((n, 1))  # n x 1 tensor
    y = (x - 4) * (x - 8) + torch.randn(x.size())  # n x 1 tensor

    model = SquareRegression()

    criterion = nn.MSELoss()
    optimizer = torch.optim.SGD(model.parameters(), lr=2e-5)

    num_epochs = 20000
    for epoch in range(num_epochs):
        inputs, targets = Variable(x), Variable(y)

        out = model(inputs)
        loss = criterion(out, targets)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if (epoch + 1) % 100 == 0:
            print('Epoch[{}/{}], loss:{:.6f}'.format(epoch + 1, num_epochs, loss.item()))

    for name, param in model.named_parameters():
        print(name, param.data)

    predict = model(x)

    plt.plot(x.numpy(), y.numpy(), 'ro', label='Original Data')
    plt.plot(x.numpy(), predict.data.numpy(), label='Fitting Line')
    plt.show()

输出结果如下：

Epoch[100/20000], loss:448.569519
Epoch[200/20000], loss:444.616638
Epoch[300/20000], loss:441.241089
Epoch[400/20000], loss:438.343903
Epoch[500/20000], loss:435.845673
Epoch[600/20000], loss:433.682007
Epoch[700/20000], loss:431.799835
Epoch[800/20000], loss:430.154999
Epoch[900/20000], loss:428.709595
Epoch[1000/20000], loss:427.431366
Epoch[1100/20000], loss:426.291718
Epoch[1200/20000], loss:425.265594
Epoch[1300/20000], loss:424.330353
Epoch[1400/20000], loss:423.465973
Epoch[1500/20000], loss:422.654541

... ... ... ...

Epoch[19400/20000], loss:1.044041
Epoch[19500/20000], loss:1.044041
Epoch[19600/20000], loss:1.044041
Epoch[19700/20000], loss:1.044041
Epoch[19800/20000], loss:1.044041
Epoch[19900/20000], loss:1.044041
Epoch[20000/20000], loss:1.044041
linear1.weight tensor([[0.7155]])
linear1.bias tensor([-5.7249])
linear2.weight tensor([[1.4002]])
linear2.bias tensor([-5.6002])

生成图像如下：

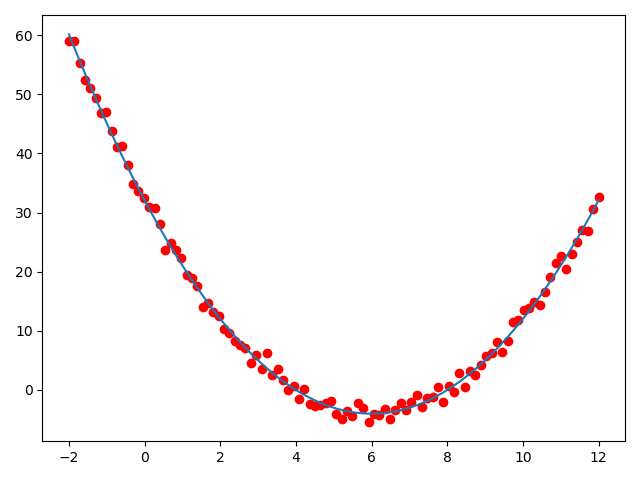
可以发现，我们生成的拟合解如下

$$\begin{cases} w_1 &= 0.7155 \\ b_1 &= -5.7249 \\ w_2 &= 1.4002 \\ b_2 &= -5.6002 \end{cases}$$

所得到的函数为

$$\begin{aligned} h(x) &= \left( w_1 x + b_1 \right) \left( w_2 x + b_2 \right) \\ &= \left( 0.7155 x - 5.7249 \right) \left( 1.4002 x - 5.6002 \right) \\ &= 1.0018431 x^2 - 12.02294808 x + 32.06058498 \end{aligned}$$

和原公式$f(x) = x^2 - 12 x + 32$已经十分接近，图像上的拟合结果也与期望结果基本一致。而且训练速度还得到了大幅度的提高（原本进行了500000次，这次在使用同样learning rate的情况下，只进行了20000次就达到了类似的效果。

其他

关于Linear

通过阅读源码可以发现，Linear内含两个最为关键的参数：weight和bias。一定程度上可以理解为所构建的线性函数公式为

$$f(x) = wx + b$$

以此类推并扩展，在2输入（in_features == 2）3输出（out_features == 3）的时候，公式为：

$$\begin{cases} f_1(x) &= w_{1, 1} x_1 + w_{1, 2} x_2 + b_1 \\ f_2(x) &= w_{2, 1} x_1 + w_{2, 2} x_2 + b_2 \\ f_3(x) &= w_{3, 1} x_1 + w_{3, 2} x_2 + b_3 \end{cases}$$

其中$w$和$b$都将以Tensor的格式，作为weight和bias进行存储，前向传播的时候则会进行矩阵运算并生成计算图。