【学习笔记】深度学习 demo1 线性回归

本人近期开始尝试基于pytorch框架，从原理上理解深度学习。在这几个demo中将会展示一些基本的操作及其效果，并基于个人的一点粗浅理解进行原理描述，如有不当之处还请指正。

在本demo中，我们所使用的线性函数为

\[f(x) = 3 x + 10 + rand \]

其中\(rand\)表示一个满足标准正态分布\(N\left(0, 1\right)\)的随机数（平均值为0，方差为1）

基于Parameter手动构建

我们可以使用nn.Parameter工具，手动构建公式以实现线性回归。

一个线性函数的基本结构如下

\[g(x) = a x + b \]

其中包含两个参数\(a\)、\(b\)。

代码如下：

import matplotlib.pyplot as plt
import torch
from torch import nn
from torch.autograd import Variable


class SquareRegression(nn.Module):
    def __init__(self):
        nn.Module.__init__(self)
        self.a = nn.Parameter(torch.randn(1, 1), requires_grad=True)  # 1 x 1
        self.b = nn.Parameter(torch.randn(1, 1), requires_grad=True)  # 1 x 1

    def forward(self, x_):
        _t = x_.mm(self.a)                # n x 1
        return _t + self.b.expand_as(_t)  # n x 1


if __name__ == "__main__":
    n = 100
    x = torch.linspace(-2, 12, n).resize_((n, 1))   # n x 1 tensor
    y = 3 * x + 10 + torch.randn(x.size())          # n x 1 tensor

    model = SquareRegression()

    criterion = nn.MSELoss()
    optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)

    num_epochs = 20000
    for epoch in range(num_epochs):
        inputs, targets = Variable(x), Variable(y)

        out = model(inputs)
        loss = criterion(out, targets)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if (epoch + 1) % 100 == 0:
            print('Epoch[{}/{}], loss:{:.6f}'.format(epoch + 1, num_epochs, loss.item()))

    for name, param in model.named_parameters():
        print(name, param.data)

    predict = model(x)

    plt.plot(x.numpy(), y.numpy(), 'ro', label='Original Data')
    plt.plot(x.numpy(), predict.data.numpy(), label='Fitting Line')
    plt.show()

输出结果如下：

Epoch[100/20000], loss:23.441666
Epoch[200/20000], loss:20.163355
Epoch[300/20000], loss:17.363503
Epoch[400/20000], loss:14.972251
Epoch[500/20000], loss:12.929962
Epoch[600/20000], loss:11.185717
Epoch[700/20000], loss:9.696020
Epoch[800/20000], loss:8.423729
Epoch[900/20000], loss:7.337113
Epoch[1000/20000], loss:6.409071
Epoch[1100/20000], loss:5.616467
Epoch[1200/20000], loss:4.939533
Epoch[1300/20000], loss:4.361391
Epoch[1400/20000], loss:3.867616
Epoch[1500/20000], loss:3.445905

... ... ... ... 

Epoch[19000/20000], loss:0.977931
Epoch[19100/20000], loss:0.977931
Epoch[19200/20000], loss:0.977931
Epoch[19300/20000], loss:0.977931
Epoch[19400/20000], loss:0.977931
Epoch[19500/20000], loss:0.977931
Epoch[19600/20000], loss:0.977931
Epoch[19700/20000], loss:0.977931
Epoch[19800/20000], loss:0.977931
Epoch[19900/20000], loss:0.977931
Epoch[20000/20000], loss:0.977931
a tensor([[2.9913]])
b tensor([[10.1255]])

生成图像如下：

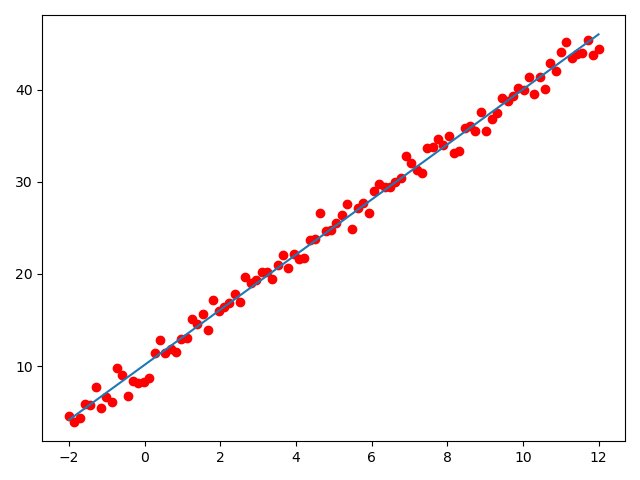
可以发现，我们生成的拟合解如下：

\[\begin{cases} a &= 2.9913 \\ b &= 10.1255 \end{cases} \]

所得到的函数为

\[\begin{aligned} g(x) &= a x + b \\ &= 2.9913 x + 10.1255 \end{aligned} \]

和原公式\(f(x) = 3x + 10\)相比已经十分接近，图像上的拟合结果也与期望结果基本一致。

基于Linear构建

实际上，pytorch已经为我们封装了nn.Linear工具实现线性回归。

一个线性函数的基本结构如下

\[h(x) = w x + b \]

其中包含两个参数\(w\)、\(b\)，分别对应nn.Linear中的weight和bias两个核心参数。

代码如下：

import matplotlib.pyplot as plt
import torch
from torch import nn
from torch.autograd import Variable


class SquareRegression(nn.Module):
    def __init__(self):
        nn.Module.__init__(self)
        self.linear = nn.Linear(1, 1)  # 1 x 1

    def forward(self, x_):
        return self.linear(x_)  # n x 1


if __name__ == "__main__":
    n = 100
    x = torch.linspace(-2, 12, n).resize_((n, 1))  # n x 1 tensor
    y = 3 * x + 10 + torch.randn(x.size())         # n x 1 tensor

    model = SquareRegression()

    criterion = nn.MSELoss()
    optimizer = torch.optim.SGD(model.parameters(), lr=1e-3)

    num_epochs = 20000
    for epoch in range(num_epochs):
        inputs, targets = Variable(x), Variable(y)

        out = model(inputs)
        loss = criterion(out, targets)

        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if (epoch + 1) % 100 == 0:
            print('Epoch[{}/{}], loss:{:.6f}'.format(epoch + 1, num_epochs, loss.item()))

    for name, param in model.named_parameters():
        print(name, param.data)

    predict = model(x)

    plt.plot(x.numpy(), y.numpy(), 'ro', label='Original Data')
    plt.plot(x.numpy(), predict.data.numpy(), label='Fitting Line')
    plt.show()

输出结果如下：

Epoch[100/20000], loss:40.807762
Epoch[200/20000], loss:34.994335
Epoch[300/20000], loss:30.029305
Epoch[400/20000], loss:25.788853
Epoch[500/20000], loss:22.167242
Epoch[600/20000], loss:19.074156
Epoch[700/20000], loss:16.432467
Epoch[800/20000], loss:14.176275
Epoch[900/20000], loss:12.249363
Epoch[1000/20000], loss:10.603661
Epoch[1100/20000], loss:9.198134
Epoch[1200/20000], loss:7.997722
Epoch[1300/20000], loss:6.972489
Epoch[1400/20000], loss:6.096869
Epoch[1500/20000], loss:5.349041

... ... ... ...

Epoch[19000/20000], loss:0.972535
Epoch[19100/20000], loss:0.972535
Epoch[19200/20000], loss:0.972535
Epoch[19300/20000], loss:0.972535
Epoch[19400/20000], loss:0.972535
Epoch[19500/20000], loss:0.972535
Epoch[19600/20000], loss:0.972535
Epoch[19700/20000], loss:0.972535
Epoch[19800/20000], loss:0.972535
Epoch[19900/20000], loss:0.972535
Epoch[20000/20000], loss:0.972535
linear.weight tensor([[2.9816]])
linear.bias tensor([10.3128])

生成图像如下：

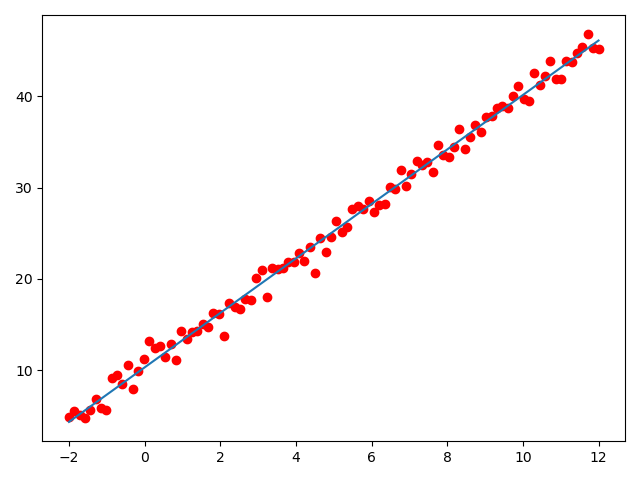
可以发现，我们生成的拟合解如下

\[\begin{cases} w &= 2.9816 \\ b &= 10.3128 \end{cases} \]

所得到的函数为

\[\begin{aligned} h(x) &= w x + b \\ & = 2.9816 x + 10.3128 \end{aligned} \]

和原公式\(f(x) = 3x + 10\)相比已经十分接近，图像上的拟合结果也与期望结果基本一致。

其他

对机器学习的一些基本理解

• 机器学习的本质是函数拟合。

• 机器学习的最基本思路，就是通过一个预定义的损失函数（loss function，用于量化描述拟合结果与实际期望结果的差异），和预定义的计算模型（线性函数、二次函数、CNN等），利用反向传播求导机制，通过梯度下降法对当前的拟合结果进行不断地优化（准确的说，是对损失函数进行不断地优化使之尽可能小）。

  • 简单来说，有两个最核心的基本要素：
    • 损失函数的定义
    • 计算模型的定义

• 通过机器学习，我们可以获得一个函数意义上的局部最优解，而无法保证所获拟合结果为复杂函数环境下的全局最优。