计算2篇文本的文本相似度（python实现）

 

引言

给定两个文本文件（比如2018年政府工作报告.txt与2019年政府工作报告.txt），怎么计算两者的相似度有多大？这是文本挖掘的一个任务，本篇将使用的方法思想如下：

• 使用jieba包分别对两篇中文txt文件进行分词，得如['今天', '我', '遇到', '一只', '蹦蹦跳跳', '的', '兔子']的两个字符串数组;*
• 对得到的分词后的数组通过进行词袋模型统计，得到他们每个词在文中出现的次数向量；
• 对得到的两个次数的矩阵进行余弦相似度计算，得到余弦相似度作为它们的文本相似度。

理论知识

一、词袋模型

文档内容(以下均简称为文档)中出现频率越高的词项，越能描述该文档（不考虑停用词）。因此可以统计每个词项在每篇文档中出现的次数，即词项频率，记为

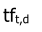
，其中t 为词项，d为文档。获得文档中每个词的 tf 权重，一篇文档则转换成了词-权重的集合，通常称为词袋模型（bag of words model）。我们用词袋模型来描述一篇文档 。词袋的含义就是说，像是把一篇文档拆分成一个一个的词条，然后将它们扔进一个袋子里。在袋子里的词与词之间是没有关系的。因此词袋模型中，词项在文档中出现的次序被忽略，出现的次数被统计。例如，“a good book” 和“book good a” 具有同样的意义。将词项在每篇文档中出现的次数保存在向量中，这就是这篇文档的文档向量。

二、余弦相似度计算

前面提出了文档向量的概念。其中每个分量代表词项在文档中的相对重要性。一系列文档在同一向量空间的表示称为 VSM（Vector Space Model）。VSM 是词袋模型。向量空间模型是信息检索、文本分析中基本的模型。通过该模型，可以进行有序文档检索、文档聚类、文档分类等。当然，现在的研究有新发展。出现了很多模型代替VSM。每篇文档在VSM中用向量表示，那么计算两篇文档的相似度自然的想到用两个向量的差值。但是，可能存在的情况是。如果两篇相似的文档，由于文档长度不一样。他们的向量的差值会很大。余弦相似度是使用的非常广泛的计算两个向量相似度的公式，它可以去除文档长度的影响。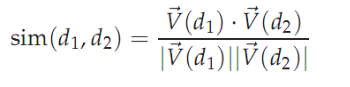

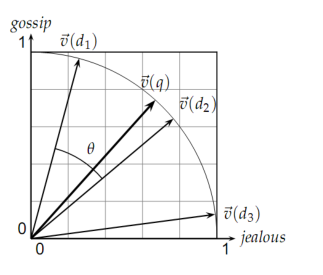
公式的分母是两个向量的欧几里得长度之积，分子是两个向量的内积。这样计算得到的sim实际上就是两个欧式归一化的向量之间的夹角的余弦。如下图：

python实现及注释

import jieba
import math
import re
#读入两个txt文件存入s1,s2字符串中
s1 = open('rdbg2018.txt','r').read()
s2 = open('rdbg2019.txt','r').read()

#利用jieba分词与停用词表，将词分好并保存到向量中
stopwords=[]
fstop=open('stop_words.txt','r',encoding='utf-8-sig')
for eachWord in fstop:
    eachWord = re.sub("\n", "", eachWord)
    stopwords.append(eachWord)
fstop.close()
s1_cut = [i for i in jieba.cut(s1, cut_all=True) if (i not in stopwords) and i!='']
s2_cut = [i for i in jieba.cut(s2, cut_all=True) if (i not in stopwords) and i!='']
word_set = set(s1_cut).union(set(s2_cut))

#用字典保存两篇文章中出现的所有词并编上号
word_dict = dict()
i = 0
for word in word_set:
    word_dict[word] = i
    i += 1


#根据词袋模型统计词在每篇文档中出现的次数，形成向量
s1_cut_code = [0]*len(word_dict)

for word in s1_cut:
    s1_cut_code[word_dict[word]]+=1

s2_cut_code = [0]*len(word_dict)
for word in s2_cut:
    s2_cut_code[word_dict[word]]+=1

# 计算余弦相似度
sum = 0
sq1 = 0
sq2 = 0
for i in range(len(s1_cut_code)):
    sum += s1_cut_code[i] * s2_cut_code[i]
    sq1 += pow(s1_cut_code[i], 2)
    sq2 += pow(s2_cut_code[i], 2)

try:
    result = round(float(sum) / (math.sqrt(sq1) * math.sqrt(sq2)), 3)
except ZeroDivisionError:
    result = 0.0
print("\n余弦相似度为：%f"%result)

 

 

参考文章

 

词袋模型

余弦相似度