python实现一般最小二乘系统辨识方法
问题:
对于一个未知参数的系统,往往需要用到系统辨识的方法,例如对于一个单输入单输出系统:
Z(k)+a1*Z(k-1)+a2*Z(k-2)=b1*U(k-1)+b2*U(k-2)+V(k)
其中:V(k)=c1*v(k)+c2*v(k-1)+c3*v(k-3)
输入信号采用四阶幅值为1的M序列,高斯噪声v(k)均值为0,方差为0.1。
假设真值为a1=1.6,a2=0.7,b1=1.0,b2=0.4,c1=1.0,c2=1.6,c3=0.7。需要对以上参数进行辨识。
方法:
一般最小二乘法是系统辨识中最简单的辨识方法之一,其MATLAB实现方法十分简单,我发现网上一大把,所以我决定“翻译”一个python版的一般最小二乘辨识方法供读者参考。
本文用到的库:
import numpy as np import matplotlib.pyplot as plt from operator import xor from numpy.linalg import inv
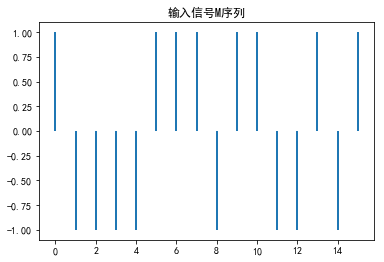
M序列的产生:
在python中,M序列的产生方法与matlab类似,先产生随机数,然后采用四阶移位寄存器滤波变换,得到我们想要的M序列。
#M序列产生 L=16 #设置M序列周期 #定义初始值 y=np.zeros(L) u=np.zeros(L) y1=1 y2=1 y3=1 y4=0 for i in range(0,L): x1=xor(y3,y4) x2=y1 x3=y2 x4=y3 y[i]=y4 if y[i]>0.5: u[i]=-1 else: u[i]=1 y1=x1 y2=x2 y3=x3 y4=x4 plt.figure(num=2) x=np.linspace(0,15,16) plt.bar(x,u,width=0.1) plt.title('输入信号M序列')
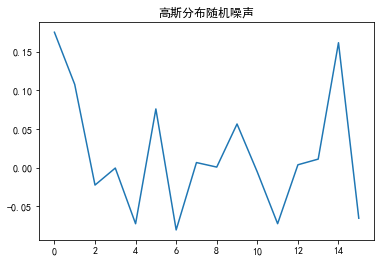
高斯分布噪声:
这里采用的是random库中的函数,可以看到,我们设置的均值为0,方差为0.1。
#产生一组16个N(0,1)的高斯分布的随机噪声
mu=0
sigma=0.1
samplenum=16
n=np.random.normal(mu,sigma,samplenum)
plt.figure(num=1)
plt.plot(n)
plt.title("高斯分布随机噪声")
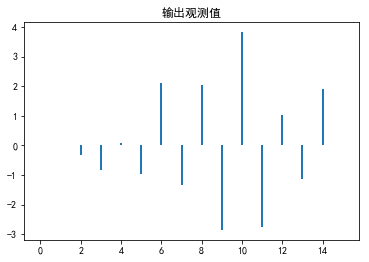
最小二乘辨识程序:
#最小二乘辨识过程 z=np.zeros(16) for k in range(2,15): z[k]=-1.6*z[k-1]-0.7*z[k-2]+1.0*u[k-1]+0.4*u[k-2]+1.0*n[k]+1.6*n[k-1]+0.7*n[k-2] plt.figure(num=3) plt.bar(x,z,width=0.1) plt.title('输出观测值') H=np.array([[-z[1],-z[0],u[1],u[0]],[-z[2],-z[1],u[2],u[1]],[-z[3],-z[2],u[3],u[2]],[-z[4],-z[3],u[4],u[3]],[-z[5],-z[4],u[5],u[4]],[-z[6],-z[5],u[6],u[5]],[-z[7],-z[6],u[7],u[6]],[-z[8],-z[7],u[8],u[7]],[-z[9],-z[8],u[9],u[8]],[-z[10],-z[9],u[10],u[9]],[-z[11],-z[10],u[11],u[10]],[-z[12],-z[11],u[12],u[11]],[-z[13],-z[12],u[13],u[12]],[-z[14],-z[13],u[14],u[13]]]) Z=np.array([z[2],z[3],z[4],z[5],z[6],z[7],z[8],z[9],z[10],z[11],z[12],z[13],z[14],z[15]]) In_1=np.transpose(H) In_2=np.dot(In_1,H) In_3=inv(In_2) In_4=np.dot(In_3,In_1) c=np.dot(In_4,Z)
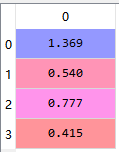
分离参数:
#分离参数并显示 a1=c[0] a2=c[1] b1=c[2] b2=c[3] print("a1的值是:",a1) print("a2的值是:",a2) print("b1的值是:",b1) print("b2的值是:",b2)
注意:
由于在python中plt的库是不支持中文的,所以要加上这些代码,保证输出的图片标题的中文显示正常。
#显示中文字体 plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签 plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
结果:
在网上找了半天python画针状图的资料,发现没有。。所以强行用瘦了的柱状图表示针状图了。
总结:
可以看出Python写的系统辨识误差还是有一些的,不过也是受到一般最小二乘参数辨识方法的限制,如果采用递推最小二乘,增广最小二乘等方法可能会进一步提高准确性。笔者尝试过递推最小二乘,但是与MATLAB相比,其代码量大大增加,因此在系统辨识方法上,不建议都用Python来写,MATLAB是个不错的选择。当然,喜欢写python的话,这都不是问题。
代码全文:
1 # -*- coding: utf-8 -*- 2 """ 3 Created on Wed Sep 20 16:11:27 2017 4 @author: Hangingter 5 """ 6 #一般最小二乘辨识 7 8 #导入相应科学计算的包 9 import numpy as np 10 import matplotlib.pyplot as plt 11 from operator import xor 12 from numpy.linalg import inv 13 14 #显示中文字体 15 plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签 16 plt.rcParams['axes.unicode_minus']=False #用来正常显示负号 17 #产生一组16个N(0,1)的高斯分布的随机噪声 18 mu=0 19 sigma=0.1 20 samplenum=16 21 n=np.random.normal(mu,sigma,samplenum) 22 plt.figure(num=1) 23 plt.plot(n) 24 plt.title("高斯分布随机噪声") 25 #M序列产生 26 L=16 27 #设置M序列周期 28 #定义初始值 29 y=np.zeros(L) 30 u=np.zeros(L) 31 y1=1 32 y2=1 33 y3=1 34 y4=0 35 for i in range(0,L): 36 x1=xor(y3,y4) 37 x2=y1 38 x3=y2 39 x4=y3 40 y[i]=y4 41 if y[i]>0.5: 42 u[i]=-1 43 else: 44 u[i]=1 45 y1=x1 46 y2=x2 47 y3=x3 48 y4=x4 49 plt.figure(num=2) 50 x=np.linspace(0,15,16) 51 plt.bar(x,u,width=0.1) 52 plt.title('输入信号M序列') 53 #最小二乘辨识过程 54 z=np.zeros(16) 55 56 for k in range(2,15): 57 z[k]=-1.6*z[k-1]-0.7*z[k-2]+1.0*u[k-1]+0.4*u[k-2]+1.0*n[k]+1.6*n[k-1]+0.7*n[k-2] 58 59 plt.figure(num=3) 60 plt.bar(x,z,width=0.1) 61 plt.title('输出观测值') 62 63 H=np.array([[-z[1],-z[0],u[1],u[0]],[-z[2],-z[1],u[2],u[1]],[-z[3],-z[2],u[3],u[2]],[-z[4],-z[3],u[4],u[3]],[-z[5],-z[4],u[5],u[4]],[-z[6],-z[5],u[6],u[5]],[-z[7],-z[6],u[7],u[6]],[-z[8],-z[7],u[8],u[7]],[-z[9],-z[8],u[9],u[8]],[-z[10],-z[9],u[10],u[9]],[-z[11],-z[10],u[11],u[10]],[-z[12],-z[11],u[12],u[11]],[-z[13],-z[12],u[13],u[12]],[-z[14],-z[13],u[14],u[13]]]) 64 Z=np.array([z[2],z[3],z[4],z[5],z[6],z[7],z[8],z[9],z[10],z[11],z[12],z[13],z[14],z[15]]) 65 66 In_1=np.transpose(H) 67 In_2=np.dot(In_1,H) 68 In_3=inv(In_2) 69 In_4=np.dot(In_3,In_1) 70 c=np.dot(In_4,Z) 71 72 #分离参数并显示 73 a1=c[0] 74 a2=c[1] 75 b1=c[2] 76 b2=c[3] 77 print("a1的值是:",a1) 78 print("a2的值是:",a2) 79 print("b1的值是:",b1) 80 print("b2的值是:",b2)
参考:
MATLAB版的系统辨识一般最小二乘方法:
http://blog.csdn.net/sinat_20265495/article/details/51426537



 浙公网安备 33010602011771号
浙公网安备 33010602011771号