牛客网字节跳动2018校招算法方向（第一批）第一题「最大点集合」题解

今天到实验室想着做一题C++笔试题玩玩，没想到费了好长时间才把这道这么简单的题做出来。

题目如下，具体见图。

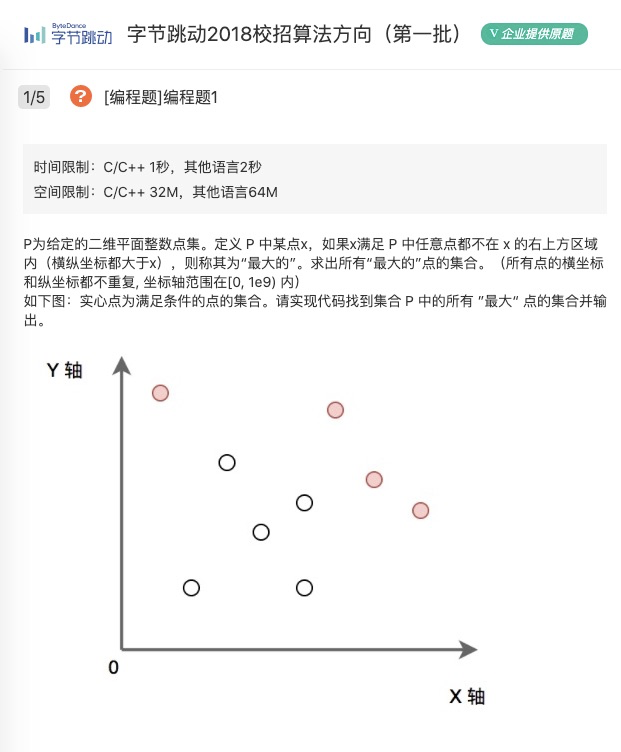
P为给定的二维平面整数点集。定义 P 中某点x，如果x满足 P 中任意点都不在 x 的右上方区域内（横纵坐标都大于x），则称其为“最大的”。求出所有“最大的”点的集合。（所有点的横坐标和纵坐标都不重复, 坐标轴范围在[0, 1e9) 内）

如下图：实心点为满足条件的点的集合。请实现代码找到集合 P 中的所有 ”最大“ 点的集合并输出。

 

 

第一行输入点集的个数 N， 接下来 N 行，每行两个数字代表点的 X 轴和 Y 轴。 
对于 50%的数据, 1 <= N <= 10000; 
对于 100%的数据, 1 <= N <= 500000; 

输出描述:

输出“最大的” 点集合， 按照 X 轴从小到大的方式输出，每行两个数字分别代表点的 X 轴和 Y轴。

样例：

  

题解：

题目的要求多看几眼应该可以看得明白，就是要找到所有满足“最大”的点，比如A点（Xa,Ya），当我们遍历除了A以外其他所有的坐标的时候，没有任何一个坐标的x比Xa大且y比Ya大。

这道题看上去第一想法就是暴力两个循环就可以解决，遍历每一个坐标A，再对比剩余其他的所有坐标，如果坐标A满足“最大”，那就把坐标A存在我们的结果里，最后再排序输出。

但是这样做一定不满足时空复杂度的要求，我也试了一下暴力两个循环来做，只能通过50%的测试样例，时间复杂度O（N^2+NlogN），这肯定是不行的。

 

仔细思考就会发现本题一定要先排序，因为我们要找的点，横坐标和纵坐标中至少有一个要比其他所有的点的坐标大，如果我们按横坐标排序，从小到大看，那么如果要成为“最大”集的一员，它的纵坐标一定要比排在它后面的所有数都要大。

举个例子：

输入：（1，2）、（8，9）、（12，7）、（4，5）、（7，13）

按横坐标排序后：（1，2）、（4，5）、（7，13）、（8，9）、（12，7）

如果（7，13）要成为“最大”集的一员，它的横坐标已经大于前面的所有数的横坐标了，只需要纵坐标大于后面的所有数的纵坐标（13满足），因此（7，13）属于“最大”集。

因此我们可以一次循环解决，只需要遍历所有按横坐标排序后的点，如果当前点的纵坐标大于后面的所有点的纵坐标（即大于后面所有点的最大纵坐标），那么这个点就一定属于“最大”集。

但是遍历的同时会带来一个问题，因为我需要比较的是后面的点，因此正向遍历只能记录前面点的最大纵坐标，所以我们需要采用反向遍历的方法。

排序比较麻烦，我直接使用了C++的map，存进去之后直接按照横坐标排好序，只需要直接反向遍历即可，map的反向遍历我也是第一次用。

上代码：

#include<map>
#include<iostream>
using namespace std;
int main(){
    int n;
    map<int,int>dots;  
    cin>>n;
    int x,y;
    for(int i=0;i<n;i++){
        cin>>x>>y;
        dots[x]=y;  //存储所有的点，直接按横坐标排好序了
    }
    int max_y=dots.end()->second;   //首先让最后一个点的纵坐标作为最大纵坐标
    //反向遍历所有的点（已经按横坐标排序）
    for(map<int,int>::reverse_iterator rit=dots.rbegin();rit!=dots.rend();rit++)
{
        //如果遇到更大的纵坐标就更新最大纵坐标
        if(rit->second>=max_y){
            max_y = rit->second;
        }
        else{
            //否则这个点就不属于“最大”集，从点集里面移除出去
            dots.erase(rit->first);
            //由于删了一个点，但是指针依然会指向下一个元素，所以让指针下标减一
            rit--;  
        }
    }
    //剩下来的就都是“最大”集了，直接输出
    for(auto i:dots){
        //使用cout非常耗时只能通过80%
        //cout<<i.first<<" "<<i.second<<endl;
        printf("%d %d\n", i.first, i.second);
    }
}