P5658 CSP-S2019括号树

[CSP-S2019] 括号树 （傻逼绿题

题目背景

本题中合法括号串的定义如下：

1. () 是合法括号串。
2. 如果 A 是合法括号串，则 (A) 是合法括号串。
3. 如果 A，B 是合法括号串，则 AB 是合法括号串。

本题中子串与不同的子串的定义如下：

1. 字符串 S 的子串是 S 中连续的任意个字符组成的字符串。S 的子串可用起始位置 \(l\) 与终止位置 \(r\) 来表示，记为 \(S (l, r)\)（\(1 \leq l \leq r \leq |S |\)，\(|S |\) 表示 S 的长度）。
2. S 的两个子串视作不同当且仅当它们在 S 中的位置不同，即 \(l\) 不同或 \(r\) 不同。

题目描述

一个大小为 \(n\) 的树包含 \(n\) 个结点和 \(n − 1\) 条边，每条边连接两个结点，且任意两个结点间有且仅有一条简单路径互相可达。

小 Q 是一个充满好奇心的小朋友，有一天他在上学的路上碰见了一个大小为 \(n\) 的树，树上结点从 \(1\) ∼ \(n\) 编号，\(1\) 号结点为树的根。除 \(1\) 号结点外，每个结点有一个父亲结点，\(u\)（\(2 \leq u \leq n\)）号结点的父亲为 \(f_u\)（\(1 ≤ f_u < u\)）号结点。

小 Q 发现这个树的每个结点上恰有一个括号，可能是( 或)。小 Q 定义 \(s_i\) 为：将根结点到 \(i\) 号结点的简单路径上的括号，按结点经过顺序依次排列组成的字符串。

显然 \(s_i\) 是个括号串，但不一定是合法括号串，因此现在小 Q 想对所有的 \(i\)（\(1\leq i\leq n\)）求出，\(s_i\) 中有多少个互不相同的子串是合法括号串。

这个问题难倒了小 Q，他只好向你求助。设 \(s_i\) 共有 \(k_i\) 个不同子串是合法括号串， 你只需要告诉小 Q 所有 \(i \times k_i\) 的异或和，即：

\[(1 \times k_1)\ \text{xor}\ (2 \times k_2)\ \text{xor}\ (3 \times k_3)\ \text{xor}\ \cdots\ \text{xor}\ (n \times k_n) \]

其中 \(xor\) 是位异或运算。

输入格式

第一行一个整数 \(n\)，表示树的大小。

第二行一个长为 \(n\) 的由( 与) 组成的括号串，第 \(i\) 个括号表示 \(i\) 号结点上的括号。

第三行包含 \(n − 1\) 个整数，第 \(i\)（\(1 \leq i \lt n\)）个整数表示 \(i + 1\) 号结点的父亲编号 \(f_{i+1}\)。

输出格式

仅一行一个整数表示答案。

样例 #1

样例输入 #1

5
(()()
1 1 2 2

样例输出 #1

6

提示

【样例解释1】

树的形态如下图：

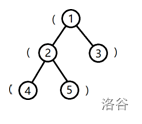
将根到 1 号结点的简单路径上的括号，按经过顺序排列所组成的字符串为 (，子串是合法括号串的个数为 \(0\)。

将根到 2 号结点的字符串为 ((，子串是合法括号串的个数为 \(0\)。

将根到 3 号结点的字符串为 ()，子串是合法括号串的个数为 \(1\)。

将根到 4 号结点的字符串为 (((，子串是合法括号串的个数为 \(0\)。

将根到 5 号结点的字符串为 (()，子串是合法括号串的个数为 \(1\)。

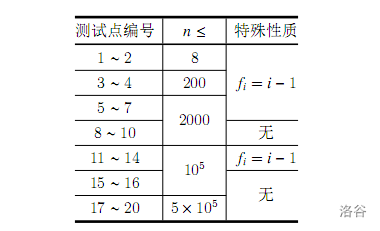
【数据范围】

思路

很容易想到，如果给出的字符串刚好是一条链，那么刚好就是一个线性dp，由于要计算每一个i结尾的字符串中答案数，所以定义\(ans[i]\)为从根节点到i这条路径上面的答案数
先从一组手搓数据出发（假设这是一条链的情况）：

\[8 ()(())() \]

相对应的答案是：

\[ans:01001203 \]

我们以第六个节点为例子，首先显而易见的：第二个节点的\(ans\)为1，并且根据题意，只有并列关系的两个合法串才多形成一个答案，所以"\(()A\)"这个串（假设A是一个合法串）中最后一个后括号的答案即为\(A\)
与这个后括号单独匹配的前括号（记其位置为\(k\)），\(k\)之前最后一个得到匹配的后括号(记为\(t\))的\(ans[t]+1\),现在一条链的情况解决了，那么如何考虑非线性结构的树呢，很简单，只要通过fa[x]数组维护一个伪线性关系就行了。至于括号匹配的方式，就用这类问题经常使用的栈来维护就行了。然后最后对于
任意的\(i\)是\(j\)的直接或间接父亲，以\(i\)结尾的必然是以\(j\)结尾的子情况(子串)，即符合前缀和的形式，最后维护一个前缀和数组就行。

需要维护的数据：

\(s[],top:\)记录未匹配的左括号
\(fa[x]：\)x节点的直接父亲
\(pre[i]:\)记录当前左括号(如果是右括号就不维护)之前最后一个得到匹配的右括号的位置
\(ans[i]:\)记录从根节点到当前节点的串中的答案值
\(sum[i]:ans[i]\)数组的树上前缀和

维护方式:

\(s[],top:\)如果当前是左括号就入栈
\(fa[x]：\)在输入的时候就可以统计
\(pre[i]:\)在函数参数内定义一个\(las\)为上一个匹配的后括号，如果\(fa[i]\)是后括号且为\(las\)，那么\(pre[i]\)为\(las\)
\(ans[i]:\)按照上文说法来统计即可
\(sum[i]:ans[i]\)数组的树上前缀和
在把所有定义为\(long long\),空间开够之后，你会发现只有85分，因为这个时候的函数是这样的：

点击查看代码

void dfs(int x,int las)
{
	if(a[x]=='(')
	{
		if(a[fa[x]]==')'&&las==fa[x])pre[x]=fa[x];
		s[++top]=x;
	}
	else
	{
		if(top==0)ans[x]=0;
		else
		{
			ans[x]=ans[pre[s[top]]]+1;
			top--;	
		}
	}
	sum[x]=sum[fa[x]]+ans[x];
//	printf("ans:[%d]:%d\n",x,ans[x]);
	for(int i=head[x];i;i=E[i].nex)dfs(E[i].v,(a[x]=='('?las:x));
}

这样的弊端在于什么呢：通过全局变量的\(s[i],top\)进行加加减减，可能会导致在\(dfs\)当前点\(x\)的时候，它的子树中的操作直接把\(x\)这个位置入栈的左括号给覆盖了，实际上我们应该对每一个节点都维护一个单独的栈，只是这些栈有着继承的关系，才省事只用了一个，所以我想到了回溯法来保证\(dfs\)完\(x\)的子树后当前x的栈是正确的，代码如下：

点击查看代码

void dfs(int x,int las)
{
	int mem=s[top];
	if(a[x]=='(')
	{
		if(a[fa[x]]==')'&&las==fa[x])pre[x]=fa[x];
		s[++top]=x;
	}
	else
	{
		if(top==0)ans[x]=0;
		else
		{
			ans[x]=ans[pre[s[top]]]+1;
//			for(int i=1;i<=top;i++)printf("%c",a[s[top]]);
			top--;	
		}
	}
	sum[x]=sum[fa[x]]+ans[x];
//	printf("ans[%d]:%d sum[%d]:%d\n",x,ans[x],x,sum[x]);
	for(int i=head[x];i;i=E[i].nex)
		dfs(E[i].v,(a[x]=='('?las:x));
	if(a[x]=='(')s[--top]=mem;
	else s[++top]=mem;
}

然而这样交上去依然只有\(85pts\)，为什么呢，小\(de\)一会后我发现即使是根本就没有进行出入栈操作的(\(top==0 /and/a[x]==')'\))的情况，该代码也会对当前栈进行操作，实测只要改掉这个地方，就可以\(AC\)了，比较菜，所以索性把遍历写了\(114514\)遍。。。

\(AC_{Code}\)

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=5e6; 
char a[maxn];int n;
struct Edge{int u,v,nex;}E[maxn];
int tote,head[maxn];
void add(int u,int v)
{
	E[++tote].u=u,E[++tote].v=v;
	E[tote].nex=head[u],head[u]=tote;
}
long long ans[maxn];
int pre[maxn]/*前括号i的上一个后括号*/;int fa[maxn];
int s[maxn],top;//stack
int sum[maxn];
void dfs(int x,int las)
{
//	for(int i=1;i<=top;i++)printf("%c",a[s[top]]);printf("\n");
	int mem=s[top];
	if(a[x]=='(')
	{
		if(a[fa[x]]==')'&&las==fa[x])pre[x]=fa[x];
		s[++top]=x;
		sum[x]=sum[fa[x]]+ans[x];
		for(int i=head[x];i;i=E[i].nex)dfs(E[i].v,(a[x]=='('?las:x));
		s[--top]=mem;
	}
	else
	{
		if(top==0)
		{
			ans[x]=0;	sum[x]=sum[fa[x]]+ans[x];
			for(int i=head[x];i;i=E[i].nex)dfs(E[i].v,(a[x]=='('?las:x));
		}
		else
		{
			ans[x]=ans[pre[s[top]]]+1;
			top--;	sum[x]=sum[fa[x]]+ans[x];
			for(int i=head[x];i;i=E[i].nex)
				dfs(E[i].v,(a[x]=='('?las:x));
			s[++top]=mem;
		}
	}
}
signed main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=2;i<=n;i++)
	{
		int tmp;scanf("%lld",&tmp);
		fa[i]=tmp;
		add(tmp,i);
	}
	dfs(1,0);
	long long Ans=0;
	for(int i=1;i<=n;i++)
		Ans^=(i*sum[i]);
	printf("%lld",Ans);
	return 0;
}