[OI] Kruskal 重构树
算法介绍
Kruskal 重构树用于快速判断节点的连通性.
考虑到,假如两个节点是联通的,则他们之间总会有一条边被选入最小生成树内,因此他们在最小生成树内也是联通的. 也就是说,我们可以通过求最小生成树来减少我们判断联通需要的边数.
Kruskal 重构树的思想是这样的:假如有一条生成树边 \((x,y)\),则断开 \((x,y)\),新建一个虚电 \(i\),连接 \((x,i),(y,i)\),在这样操作后,因为原生成树即为一棵树,因此新构成的图也是一棵树,并且树上任意一点的子树中的所有节点总是可达的. 这个操作可以在求生成树时同时进行.
对于带权的边,我们可以把边权直接放到点上. 注意到这样构造出来的重构树一定是二叉堆. 并且任意两点路径边权最大值为重构树上LCA的点权.
为什么是最大值?考虑到我们构建最小生成树的过程,最大的边一定会后选. 在考虑我们构建重构树的过程,后选的边总是作为新的父节点,因此两点的 LCA 即为两点间路径中最后选的那一个,即边权最大值.
注意到这一块可能是需要爆改的,改这个主要使用改最小生成树来实现,学长说跑什么生成树是需要变通的,比如要求最小边权就需要跑最大生成树,有时候还需要跑特殊生成树,只不过这个算法的思想是借助的 Kruskal 的,所以我们用最小生成树当例子.
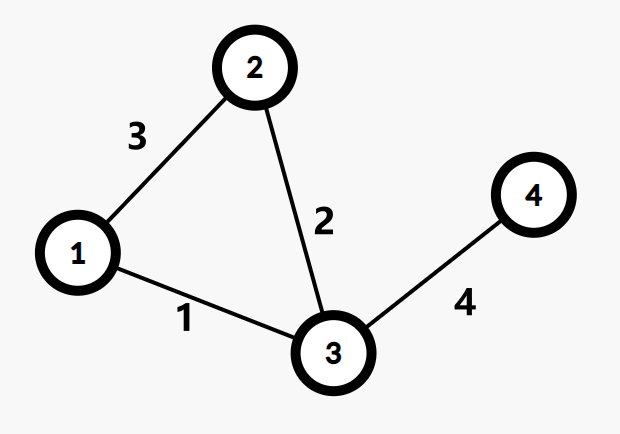
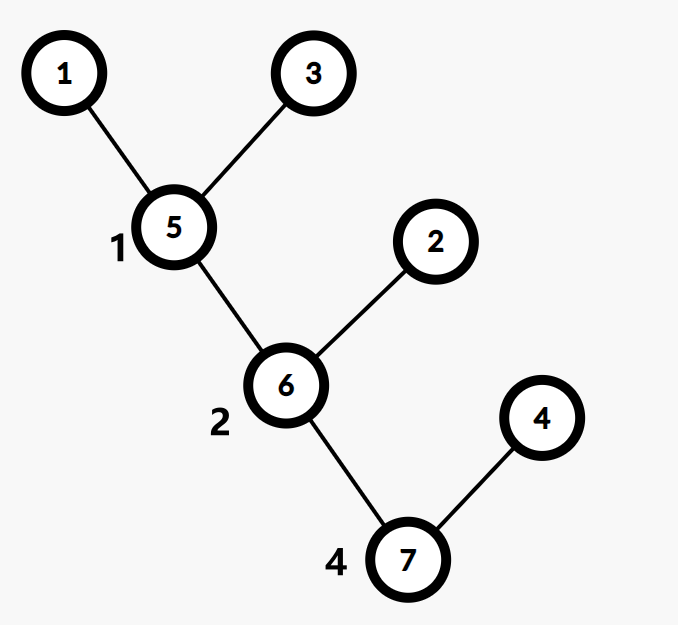
首先新建 \(n\) 个集合,每个集合恰有一个节点,点权为 \(0\)
每一次加边会合并两个集合,我们可以新建一个点,点权为加入边的边权,同时将两个集合的根节点分别设为新建点的左儿子和右儿子。然后我们将两个集合和新建点合并成一个集合。将新建点设为根
此处模板使用 \(\gt n\) 的点作为虚点.
void Kruskal(){
for(int i=1;i<=n;i++){
fa[i]=i;
}
int cnt=0;
sort(e+1,e+n+1);
for(int i=1;i<=m;i++){
int x=e[i].x, y=e[i].y, w=e[i].w;
int fx=find(x),fy=find(y);
if(fx^fy){
val[++cnt+n]=w;
fa[fx]=fa[fy]=fa[cnt+n]=now;
e[cnt+n].push_back({fx,1});
e[cnt+n].push_back({fy,1});
}
}
}
CF1706E Qpwoeirut and Vertices
这个题涉及到了重构树求最值的问题,写了比较有启发意义的爆改线段树
此题可以将时间戳设计成点权,考虑到重构树的特殊性质,我们可以将其按时间戳全部联通,根据任意两点路径边权最大值为重构树上LCA的点权,此题我们需要求的正好就是边权最大值,因此直接维护树上 LCA 即可. 取最值可以用 st 表或线段树.
这里没排序是因为时间戳是有序的,用的线段树来维护,更新子节点节点最大权值的时候也可以直接 LCA 解决,比较方便,只是常数比 LCA 大.
#include<bits/stdc++.h>
using namespace std;
int n,m,q,tot;
namespace dsu{
int fa[300001];
inline void clear(){
for(register int i=1;i<=n+m;++i){
fa[i]=i;
}
}
inline int find(int id){
if(id==fa[id]) return id;
fa[id]=find(fa[id]);
return fa[id];
}
}
vector<int>e[300001];
namespace lca{
int fa[20][300001],deep[300001];
inline void dfs(int now){
for(int i=1;i<=19;++i){
fa[i][now]=fa[i-1][fa[i-1][now]];
}
for(int i:e[now]){
deep[i]=deep[now]+1;
fa[0][i]=now;
dfs(i);
}
}
inline void prework(){
for(register int i=1;i<=19;++i){
for(register int j=1;j<=n+m;++j){
fa[i][j]=fa[i-1][fa[i-1][j]];
}
}
}
inline int lca(int x,int y){
if(deep[x]<deep[y]) swap(x,y);
for(register int i=19;i>=0;--i){
if((deep[x]-deep[y])>=(1ll<<i)){
x=fa[i][x];
}
}
if(x==y) return x;
for(register int i=19;i>=0;--i){
if(fa[i][x]!=fa[i][y]){
x=fa[i][x];y=fa[i][y];
}
}
return x==y?x:fa[0][x];
}
}
namespace stree{
#define tol (id*2)
#define tor (id*2+1)
#define mid(x,y) mid=((x)+(y))/2
struct tree{
int l,r,w;
}t[400001];
inline void build(int id,int l,int r){
t[id].l=l,t[id].r=r;if(l==r){
t[id].w=l;
return;
}
int mid(l,r);
build(tol,l,mid);
build(tor,mid+1,r);
t[id].w=lca::lca(t[tol].w,t[tor].w);
}
inline int ask(int id,int l,int r){
if(t[id].l==l and t[id].r==r) return t[id].w;
int mid(t[id].l,t[id].r);
if(r<=mid) return ask(tol,l,r);
if(l>=mid+1) return ask(tor,l,r);
return lca::lca(ask(tol,l,mid),ask(tor,mid+1,r));
}
}
namespace hdk{
namespace Iter{
void cout(std::vector<int> &_v,int _from,int _to,char _devide){std::vector<int>::iterator iter;std::vector<int>::reverse_iterator riter;
if(_from<_to){for(iter=_v.begin()+_from;iter!=_v.begin()+_to;++iter){std::cout<<*iter<<_devide;}}
else{for(riter=_v.rbegin()+_to;riter!=_v.rbegin()+_from;++riter){std::cout<<*riter<<_devide;}}}
}
template<typename T>
void memset(T a[],int _val,int _size){if(_val==0){for(T* i=a;i<=a+_size-1;++i) *i&=0;return;}for(T* i=a;i<=a+_size-1;++i)*i=_val;}
namespace fastio{
void rule(bool setting=false){std::ios::sync_with_stdio(setting);}
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-'){f=-1;}ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
inline int read(int &A){A=read();return A;}
inline char read(char &A){A=getchar();return A;}
inline void write(int A){if(A<0){putchar('-');A=-A;}if(A>9){write(A/10);}putchar(A%10+'0');}
inline void write(long long A){if(A<0){putchar('-');A=-A;}if(A>9){write(A/10);}putchar(A%10+'0');}
inline void write(char A){putchar(A);}
inline void space(){putchar(' ');}
inline void endl(){putchar('\n');}
#define w(a) write(a)
#define we(a) write(a);endl()
#define ws(a) write(a);space()
}
}
using namespace hdk::fastio;
int main(){
// freopen("lagrange1.in","r",stdin);
// freopen("hdk.out","w",stdout);
int cases;read(cases);while(cases--){
read(n);read(m);read(q);
tot=0;
dsu::clear();
for(int i=1;i<=n+m;++i){
e[i].clear();
}
for(register int i=1;i<=m;++i){
int x,y;read(x);read(y);
int fx=dsu::find(x),fy=dsu::find(y);
if(fx==fy) continue;
e[i+n].push_back(fx);
e[i+n].push_back(fy);
dsu::fa[fx]=dsu::fa[fy]=i+n;
tot=i+n;
}
lca::deep[tot]=1;
lca::dfs(tot);
// lca::prework();
stree::build(1,1,n);
for(register int i=1;i<=q;++i){
int l,r;l=read();r=read();
if(l^r){
ws(stree::ask(1,l,r)-n);
}
else{
putchar('0');putchar(' ');
}
}
endl();
}
}
[NOI2018] 归程
本题就是刚才说的那种跑最大生成树的题,而且这个题比较巧妙,跑的是关于海拔的最大生成树. 首先跑之前先把单源最短路求出来,其次按上面的套路重构出一个关于海拔的重构树,因为是最大生成树,因此可以求到路径最小值,我们需要的就是这个,因此根据路径最小值去爆搜一遍.
这道题把倍增放在询问里用,因为这个题显然是求出距离来剩下的暴跳就行了,所以 倍增主要是用来暴跳的而不是用来 LCA 的
#include<bits/stdc++.h>
using namespace std;
const int N=800001;
int n,m;
struct edge{
int to,w;
};
vector<edge>e[N];
struct aedge{
int x,y,l;
bool operator <(const aedge &A)const{
return l>A.l;
}
}E[N];
struct node{
int id,w;
bool operator <(const node &A)const{
return w>A.w;
}
};
int fa[N][21],_min[N],val[N];
namespace dsu{
int fa[N];
void clear(int n){
for(int i=1;i<=n;++i){
fa[i]=i;
}
}
int find(int id){
if(id==fa[id]) return id;
fa[id]=find(fa[id]);
return fa[id];
}
}
namespace DIJKSTRA{
int vis[N],dis[N];
priority_queue<node>q;
void dij(){
memset(vis,0,sizeof vis);
memset(dis,0x3f,sizeof dis);
vis[1]=1;dis[1]=0;
q.push({1,dis[1]});
while(!q.empty()){
node u=q.top();q.pop();
for(edge i:e[u.id]){
if(dis[i.to]>dis[u.id]+i.w){
dis[i.to]=dis[u.id]+i.w;
q.push({i.to,dis[i.to]});
}
}
}
}
}
bool vvis[N];
void dfs(int now,int last){
if(vvis[now]) return;
vvis[now]=true;
fa[now][0]=last;
_min[now]=DIJKSTRA::dis[now];
for(int i=1;i<=20;++i){
fa[now][i]=fa[fa[now][i-1]][i-1];
}
for(edge i:e[now]){
if(i.to!=last){
dfs(i.to,now);
_min[now]=min(_min[now],_min[i.to]);
}
}
}
int cnt;
int main(){
int cases;scanf("%d",&cases);while(cases--){
scanf("%d %d",&n,&m);
memset(_min,0,sizeof _min);
memset(fa,0,sizeof fa);
for(int i=1;i<=N;++i){
e[i].clear();
}
for(int i=1;i<=m;++i){
int x,y,l,a;scanf("%d %d %d %d",&x,&y,&l,&a);
E[i]={x,y,a};
e[x].push_back({y,l});
e[y].push_back({x,l});
}
DIJKSTRA::dij();
sort(E+1,E+m+1);
dsu::clear(N);
for(int i=1;i<=N;++i){
e[i].clear();
}
int now=n;
for(int i=1;i<=m;++i){
int x=E[i].x,y=E[i].y,w=E[i].l;
int fx=dsu::find(x);
int fy=dsu::find(y);
if(fx^fy){
val[++now]=w;
dsu::fa[fx]=dsu::fa[fy]=dsu::fa[now]=now;
e[now].push_back({fx,1});
e[now].push_back({fy,1});
}
}
memset(vvis,false,sizeof vvis);
dfs(now,0);
int last=0;
int q,k,s;scanf("%d %d %d",&q,&k,&s);
for(int i=1;i<=q;++i){
int x,y,v,p;
scanf("%d %d",&x,&y);
v=(x+k*last-1)%n+1;
p=(y+k*last)%(s+1);
for(int j=20;j>=0;--j){
if(fa[v][j] and val[fa[v][j]]>p) v=fa[v][j];
}
printf("%d\n",last=_min[v]);
}
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号