[OI] 分层图最短路

什么是分层图最短路

分层图是指有很多个平行的图，各个平行的图之间有特殊的连接边。

分层图最短路，是在原有的求图中某两个点之间的最短路基础上增加一个条件——可以选择 \(k\) 条路，将它们的路径长度变为零（或者其他操作，常见的还是变为0，其他的我们暂不考虑），这样即可通过缩短路径长度，找出在该条件下的最短路。

为什么它叫分层图最短路

一般来说，因为我们并不知道一条边究竟被修改了还是没有，因此不如赋予它两个权值，像这样 同一条边同时有两种及以上不能同时选择的权值 我们就把这几条边看作是在不同的“图层”，这样我们就可以通过一些特殊变形来跑最短路了.

构建分层图最短路

首先，分层图要有“图层”，因此我们需要根据题意来赋予每个图层特殊的意义.

一般来说，我们有以下定义：

当对图进行 \(k\) 次操作时，分层图的图层有 \(k+1\) 层，我们设边 \(<i,j,u,v,w>\) 为从 \(u\) 到 \(v\) ,权值为 \(w\) 的有向边，且它在图层 \(i\) 到图层 \(j\) 的交界上.

那么有：

边 \(<i,i,u,v,w>\) 表示已进行了 \(i\) 次操作，且不改建当前道路，由u向v耗费w.

边 \(<i,i+1,u,v,0>\) 表示在 \(u\) 点进行一次操作，进入下一层，将该路上的 \(w[u][v]\) 变为 0 (或者其他条件).

所以，我们需要连的边就变成了：

1. 每个“图层”内部正常连边
2. 假如存在边 \(<i,i,u,v,w>\),那么连接边 \(<i,i+1,u,v,0>\) (前提是 \(i<k+1\) ).

大概像下面这样：

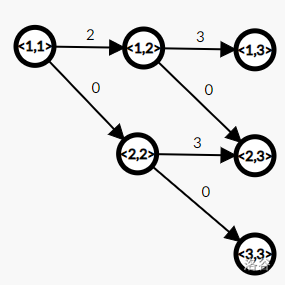
建好图后，我们再跑最短路算法就没有问题了.