比赛链接：
https://atcoder.jp/contests/abc266
C - Convex Quadrilateral
题意：
平面图上有一个四边形，按照逆时针顺序给定四个点的坐标，判断四边形是不是凸的。
思路：
求两条临边的向量积是不是 > 0 即可。
代码：
#include <bits/stdc++.h>
using namespace std;
int main(){
ios::sync_with_stdio(false);cin.tie(0);
vector <int> x(4), y(4);
for (int i = 0; i < 4; i ++ )
cin >> x[i] >> y[i];
for (int i = 0; i < 4; i ++ ){
int a = (x[(i - 1 + 4) % 4] - x[i]) * (y[(i + 1) % 4] - y[i]) - (x[(i + 1) % 4] - x[i]) * (y[(i - 1 + 4) % 4] - y[i]);
if (-a <= 0){
cout << "No\n";
return 0;
}
}
cout << "Yes\n";
return 0;
}
D - Snuke Panic (1D)
题意：
地上有五个连续的坑，序号从 0 到 4，有 \(n\) 件物品会掉落，第 \(i\) 件物品会在 \(t_i\) 秒掉到 \(x_i\) 坑，它的体积是 \(a_i\)，角色 0 秒的时候在 0 号坑，每一秒可以移动一步，问最多能接到体积总和为多少的物品。
思路：
因为上一秒的情况转移到这一秒是有限的，且没有后效性，考虑 \(dp\)。
设 \(dp[i][j]\) 表示第 \(i\) 秒到 \(j\) 号坑能获得体积为多少的物品。
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e5 + 10;
LL dp[N][5], p[N], w[N];
int main(){
ios::sync_with_stdio(false);cin.tie(0);
int n;
cin >> n;
for (int i = 1; i <= n; i ++ ){
int t, x, a;
cin >> t >> x >> a;
p[t] = x;
w[t] = a;
}
for (int i = 1; i <= 4; i ++ ){ //刚开始到不了这四个点
dp[0][i] = -1e18;
}
for (int t = 1; t <= 100000; t ++ ){
for (int i = 0; i < 5; i ++ ){
dp[t][i] = dp[t - 1][i];
if (i != 0) dp[t][i] = max(dp[t][i], dp[t - 1][i - 1]);
if (i != 4) dp[t][i] = max(dp[t][i], dp[t - 1][i + 1]);
}
dp[t][p[t]] += w[t];
}
LL ans = 0;
for (int i = 0; i <= 4; i ++ )
ans = max(ans, dp[100000][i]);
cout << ans << "\n";
return 0;
}
E - Throwing the Die
题意：
摇骰子，最多可以摇 \(n\) 轮，每回合，可以选择结束，那么当前摇出来的值就是最终的分数，也可以继续摇，问最后的最大期望分数是多少。
思路：
每次只有两个选择，继续或者结束，容易想到第 \(i\) 轮从第 \(i - 1\) 轮转移过来。
设 \(f[i]\) 表示进行了 \(i\) 轮的最大期望分数。
那么第 \(i\) 轮的最大分数就是第 \(i - 1\) 轮的最大分数或者当前这一轮的结束分数。
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
int main(){
ios::sync_with_stdio(false);cin.tie(0);
int n;
cin >> n;
function<double(int)> f = [&](int x){
if (x == 0) return 0.0;
double t = f(x - 1), res = 0;
for (int i = 1; i <= 6; i ++ )
res += max(t, i * 1.0) / 6;
return res;
};
cout << fixed << setprecision(15) << f(n) << "\n";
return 0;
}
F - Well-defined Path Queries on a Namori
题意：
给定 \(n\) 个节点，\(n\) 条双向边的图，\(q\) 次询问，问 \(u\) 到 \(v\) 的简单路径是不是只有 1 条。
思路：
\(n\) 个节点，\(n\) 条双向边的图的本质就是一棵树 + 一个环，所以先想办法把环弄出来，当度为 1，就将它入队，用 \(bfs\) 跑出来环。
当询问的两个点都在环上，显然不止一条简单路径。
当两个点不在环上，显然就一条简单路径。
当一个在环上一个不在，可能是可能不是。
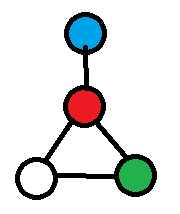
红色和蓝色只有一条简单路径，绿色和蓝色有两条。
考虑在 \(bfs\) 的时候加一个 \(dsu\)，将环上一个节点和与它连通的不在环上的节点联通起来，这样子只用判断是不是在一个连通块里面就行了。
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
struct dsu{
int n;
vector <int> p;
dsu(int n) : n(n){
p.resize(n + 1);
iota(p.begin(), p.end(), 0);
}
int get(int x){
return (x == p[x] ? x : (p[x] = get(p[x])));
}
void unite(int x, int y){
x = get(x);
y = get(y);
if (x != y){
p[x] = y;
}
}
};
int main(){
ios::sync_with_stdio(false);cin.tie(0);
int n;
cin >> n;
vector < vector<int> > e(n + 1);
vector <int> deg(n + 1);
for (int i = 0; i < n; i ++ ){
int u, v;
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
deg[u] ++ ;
deg[v] ++ ;
}
dsu d(n);
vector <bool> used(n + 1, false);
auto bfs = [&](){
queue <int> q;
for (int i = 1; i <= n; i ++ ){
if (deg[i] == 1){
q.push(i);
}
}
while(q.size()){
int u = q.front();
q.pop();
used[u] = true;
for (auto v : e[u]){
if (used[v]) continue;
d.unite(u, v);
deg[v] -- ;
if (deg[v] == 1){
q.push(v);
}
}
}
};
bfs();
int q;
cin >> q;
for (int i = 0; i < q; i ++ ){
int u, v;
cin >> u >> v;
if (d.get(u) == d.get(v)) cout << "Yes\n";
else cout << "No\n";
}
return 0;
}
