比赛链接:
https://vjudge.net/contest/509567
B - Independent Feedback Vertex Set
题意:
定义无向无环图为森林,集合中任意两点之间没有边相连的集合为独立集。
现在有 \(n\) 个点,每个点有一个权重,刚开始的图中有 1,2,3 三个点,互相之间有边相连。
按照给定的顺序依次添加点进入集合,每次告诉图中的一条边 \((y, z)\),然后向集合中加入点 \(x\),加入边 \((x, y), (x, z)\)。
从最后形成的图中找出一个独立集,使得剩下的图为森林,问这个独立集的权重最大为多少。
思路:
对于每一个新加入的点,它与图中选定的那条边的两个点不会同时选中,即 \(x\) 不会和 \(y, z\) 同时选中。
考虑染色,先将初始的三个点染不同的颜色,接下来加入的每个点就都有指定的颜色,求同一种颜色的权值之和的最大即可。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
void solve(){
LL n;
cin >> n;
vector <LL> a(n);
for (int i = 0; i < n; i ++ )
cin >> a[i];
vector <LL> color(n);
for (int i = 0; i < 3; i ++ )
color[i] = i;
for (int i = 3; i < n; i ++ ){
LL u, v;
cin >> u >> v;
u -- ; v -- ;
color[i] = 3 - color[u] - color[v];
}
vector <LL> ans(3, 0);
for (int i = 0; i < n; i ++ )
ans[color[i]] += a[i];
cout << *max_element(ans.begin(), ans.end()) << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
C - Counting Stickmen
题意:
在给定的树中找有几个下图红色节点所示的火柴人。
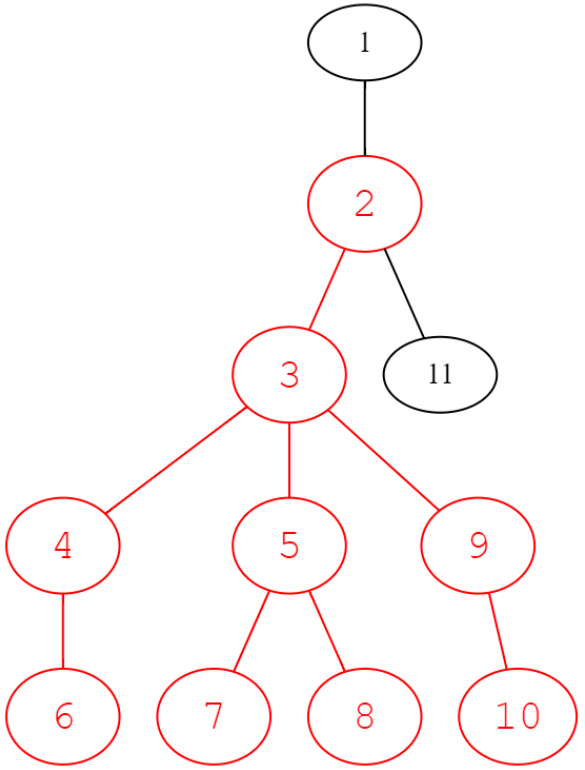
思路:
每个节点的度数减去 1 就是它作为手臂的可能,度数大于 2 的节点,它作为身体的可能为 \(C_{deg[i] - 1}^2\) 种,即减去连接边,剩余的节点选两个作为腿。
接着枚举每个点作为身体中心,计算火柴人的数量。
选择一个身体,两个手臂,除去两个手和身体,其它节点都可以作为头。
对于手,下图这种情况是不行的,要减去。
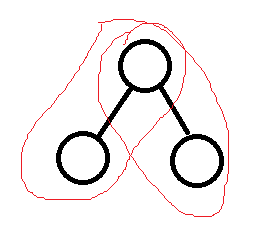
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int P = 998244353;
LL qp(LL a, LL k, LL p){
LL ans = 1;
while (k){
if (k & 1) ans = ans * a % p;
k >>= 1;
a = a * a % p;
}
return ans;
}
LL inv(LL x){
return qp(x, P - 2, P);
}
LL c2(LL x){
return x * (x - 1) % P * inv(2) % P;
}
void solve(){
LL n;
cin >> n;
vector <LL> g[n + 1], deg(n + 1);
for (int i = 0; i < n - 1; i ++ ){
LL u, v;
cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
deg[u] ++ ;
deg[v] ++ ;
}
vector <LL> hand(n + 1), body(n + 1);
for (int i = 1; i <= n; i ++ ){
hand[i] = deg[i] - 1;
if (deg[i] > 2){
body[i] = c2(deg[i] - 1);
}
}
LL ans = 0;
function<void(LL, LL)> dfs = [&](LL u, LL fa){
LL h = 0, b = 0;
for (auto v : g[u]){
h = (h + hand[v]) % P;
b = (b + body[v]) % P;
if (v == fa) continue;
dfs(v, u);
}
if (deg[u] < 4) return;
LL res = 0;
for (auto v : g[u])
res = (res + body[v] * ((c2(h - hand[v]) - (b - body[v])) % P + P) % P * (deg[u] - 3) % P ) % P;
ans = (ans + res) % P;
};
dfs(1, 0);
cout << ans << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
D - Black Magic
题意:
有四种方块:
E:左右两面全是白色
L:右边是黑色,右边是白色
R:左边是黑色,左边是白色
B:左右两面都是黑色
当黑面和黑面碰在一起的时候,这两个方块可以融合,问最小/最大的连通块是多少。
思路:
就分类讨论一下。
最小即将 \(L\) 和 \(R\) 组合,然后 \(B\) 合到其中一个上,如果 \(L\) 和 \(R\) 都没有的话,则单独算一个。
最大就是将 \(L\) 放到左边,\(R\) 放到右边,然后 \(E\) 和 \(B\) 交替。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
void solve(){
LL E, L, R, B;
cin >> E >> L >> R >> B;
LL minn = E;
if (min(L, R) >= 1){
minn += max(L, R);
}
else{
minn += L + R;
if (max(L, R) == 0) minn += (B > 0);
}
LL maxn = L + R;
if (B > E){
maxn += E * 2 + 1;
}
else{
maxn += B + E;
}
cout << minn << " " << maxn << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
F - Sumire
题意:
计算 \(\sum_{i = l}^r f^k (i, B, d)\)。
\(f(i, B, d)\) 表示在 \(x\) 的 \(B\) 进制下,\(d\) 出现的次数。
在本题中 \(0^0 = 0\)。
思路:
显然的数位 \(dp\)。
定义 \(dp[pos][sum][limit][zero]\) 表示枚举到第 \(pos\) 位,\(d\) 出现了 \(sum\) 次,\(limit\) 为 1 表示当前枚举的数为上限,\(zero\) 为 1 表示有前导 0。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int P = 1e9 + 7;
LL k, B, d, l, r, dp[70][70][2][2], num[70];
LL qp(LL a, LL k, LL p){
if (!a && !k) return 0; // 0 的 0 次为 0
LL ans = 1;
while (k){
if (k & 1) ans = ans * a % p;
k >>= 1;
a = a * a % p;
}
return ans;
}
LL dfs(int pos, LL sum, int limit, int zero){
if (pos == 0) return dp[pos][sum][limit][zero] = qp(sum, k, P);
if (dp[pos][sum][limit][zero] != -1) return dp[pos][sum][limit][zero];
LL ans = 0;
int up = (limit ? num[pos] : B - 1);
if (d == 0){
if (up == 0) ans = (ans + dfs(pos - 1, sum + !zero, limit, zero)) % P;
else{
ans = (ans + dfs(pos - 1, sum, limit, 0)) % P; //放up
ans = (ans + dfs(pos - 1, sum + !zero, 0, zero)) % P; //放d
ans = (ans + dfs(pos - 1, sum, 0, 0) * (up - 1) % P) % P; //放其它数
}
}
else{
if (d < up){
ans = (ans + dfs(pos - 1, sum, limit, 0)) % P; //放up(因为 d != 0,所以 up > 1)
ans = (ans + dfs(pos - 1, sum + 1, 0, 0)) % P; //放d
ans = (ans + dfs(pos - 1, sum, 0, zero)) % P; //放0
ans = (ans + dfs(pos - 1, sum, 0, 0) * (up - 2) % P) % P; //放其它数
}
else if (d == up){
ans = (ans + dfs(pos - 1, sum + 1, limit, 0)) % P; //放d
ans = (ans + dfs(pos - 1, sum, 0, zero)) % P; //放0
ans = (ans + dfs(pos - 1, sum, 0, 0) * (up - 1) % P) % P; //放其它数
}
else {
ans = (ans + dfs(pos - 1, sum, limit, 0)) % P; //放limit
ans = (ans + dfs(pos - 1, sum, 0, zero)) % P; //放0
ans = (ans + dfs(pos - 1, sum, 0, 0) * (up - 1) % P) % P; //放其他数
}
}
return dp[pos][sum][limit][zero] = ans % P;
}
LL solve(LL x){
memset(dp, -1, sizeof dp);
int len = 0;
while(x){
num[ ++ len] = x % B;
x /= B;
}
return dfs(len, 0, 1, 1);
}
void solve(){
cin >> k >> B >> d >> l >> r;
cout << ((solve(r) - solve(l - 1)) % P + P) % P << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
G - Weighted Beautiful Tree
题意:
\(n\) 个节点的树,每个节点有一个权重 \(wn_i\) 和一个系数 \(c_i\)。修改某个节点从 \(wn_u\) 变成 \(wn_{u'}\),花费为 \(c_u * \lvert wn_u - wn_{u'} \rvert\),问要让所有节点满足 min(\(wn_{u_i}, wn_{v_i}\)) <= \(w_{e_i}\) <= max(\(wn_{u_i}, wn_{v_i}\)) 的最小花费。
思路:
因为某个点的权值只可能不变,或者变成某条相邻边的权重。
定义 \(dp[u][0/1]\) 为让 \(u\) 节点权重满足小于等于/大于等于与父节点连边的权重,且子树全都符合条件的最小花费。
将所有的邻边权值加入数组中,进行排序,接着枚举每一个权重作为点的权重的最优情况。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const LL INF = 1e18;
void solve(){
int n;
cin >> n;
vector <int> c(n + 1);
for (int i = 1; i <= n; i ++ )
cin >> c[i];
vector <int> wn(n + 1);
for (int i = 1; i <= n; i ++ )
cin >> wn[i];
vector < vector < pair<int, LL> > > e(n + 1);
for (int i = 1; i < n; i ++ ){
int u, v, w;
cin >> u >> v >> w;
e[u].push_back({v, w});
e[v].push_back({u, w});
}
vector < array<LL, 2> > dp(n + 1, {INF, INF});
vector <int> fw(n + 1); //点与父节点连边的权重
fw[1] = 0;
function<void(int, int)> dfs = [&](int u, int fa){
vector < pair<LL, int> > son;
LL suf = 0;
for (auto t : e[u]){
int v = t.first, w = t.second;
if (v == fa) continue;
fw[v] = w;
dfs(v, u);
son.push_back({w, v});
suf += dp[v][1];
}
son.push_back({wn[u], 0});
son.push_back({fw[u], 0});
sort(son.begin(), son.end());
LL pre = 0;
for (int i = 0; i < son.size(); i ++ ){
int j = i;
suf -= dp[son[j].second][1];
LL t = min(dp[son[j].second][0], dp[son[j].second][1]);
while(j < (int)son.size() - 1 && son[j].first == son[j + 1].first){ //对于相同权重的边合并处理
j ++ ;
suf -= dp[son[j].second][1];
t += min(dp[son[j].second][0], dp[son[j].second][1]);
}
t += pre + suf;
if (son[j].first <= fw[u] || u == 1)
dp[u][0] = min(dp[u][0], t + c[u] * abs(wn[u] - son[j].first));
if (son[j].first >= fw[u] || u == 1)
dp[u][1] = min(dp[u][1], t + c[u] * abs(wn[u] - son[j].first));
while(i < j){
pre += dp[son[i].second][0];
i ++ ;
}
pre += dp[son[i].second][0];
}
};
dfs(1, 0);
cout << min(dp[1][0], dp[1][1]) << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
int T;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
H - Triangle Game
题意:
两个人轮流玩游戏,给定三角形的三条边 \(a\),\(b\),\(c\),每次可以将其中一条边变小,当有一个人不论怎么修改都构不成三角形的时候,判输,两个人都采取最优策略,问先手是否必胜。
思路:

代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
void solve(){
LL a, b, c;
cin >> a >> b >> c;
if ( (a - 1) ^ (b - 1) ^ (c - 1) ) cout << "Win\n";
else cout << "Lose\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号