比赛链接：
https://vjudge.net/contest/507737
A - Link with Bracket Sequence II
题意：
有一个长为 \(n\) 的括号序列 \(a\)，总共有 \(m\) 种括号。
若 \(a_i == 0\)，那么可以填任意一种括号；
若 \(a_i > 0\)，说明它是第 \(i\) 种括号的左括号。
若 \(a_i < 0\)，说明它是第 \(i\) 种括号的右括号。
输出有多少种合法括号序列。
思路：
设 \(f_{i,j}\) 表示 \([i, j]\) 为合法括号序列且 \(i\) 和 \(j\) 上括号匹配的方案数，\(g_{i,j}\) 表示 \([i, j]\) 区间形成一个合法括号序列的方案数。
当 \(i\) 和 \(j\) 上位置匹配的时候，\(f_{i,j} = g_{i,j} * num\)，\(num\) 表示 \(i\) 和 \(j\) 相互匹配的方案。
同时可以得到转移方程 \(g_{i,j} = g_{i,k} * f_{k + 1, j}\)。
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int mod = 1e9 + 7;
void solve(){
LL n, m;
cin >> n >> m;
vector <LL> a(n + 1);
for (int i = 1; i <= n; i ++ )
cin >> a[i];
if (n & 1){
cout << "0\n";
return;
}
vector < vector<LL> > f(n + 1, vector<LL>(n + 1, 0)), g(n + 1, vector<LL>(n + 1, 0));
for (int i = 0; i < n; i ++ )
g[i + 1][i] = 1;
for (int len = 2; len <= n; len += 2 ){
for (int L = 1; L + len - 1 <= n; L ++ ){
int R = L + len - 1, num = 0;
if (a[L] == 0 && a[R] == 0){
num = m;
}
else if ( (a[L] == 0 && a[R] < 0) || (a[L] > 0 && a[R] == 0) ){
num = 1;
}
else if (a[L] + a[R] == 0 && a[L] > 0){
num = 1;
}
f[L][R] = g[L + 1][R - 1] * num % mod;
for (int k = L; k <= R; k += 2)
g[L][R] = (g[L][R] + g[L][k - 1] * f[k][R]) % mod;
}
}
cout << g[1][n] << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
D - Link with Equilateral Triangle
题意：
问是否能构造一个边长为 \(n\) 的三角形，每个点中只能填充 0 或 1 或 2，满足任意一个小三角形的三点之和不是 3，同时底边上不能填 2，左斜边上不能填 0，右斜边上不能填 1。
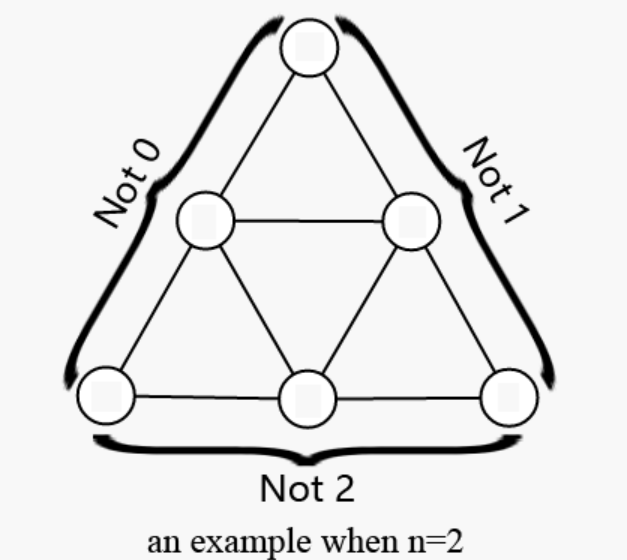
思路：
不论边长为几，都构造不出来，全部输出 No 即可。
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
void solve(){
LL n;
cin >> n;
cout << "No\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
F - BIT Subway
题意：
有 \(n\) 张票，依次购买。
当已购买的票总价超过 100 时，接下来买的票打八折。
当已购买的票总价超过 200 时，接下来买的票打五折。
\(DLee\) 认为一张票可以买一部分，即可以先买一部分让总价达到优惠价，然后打折购买，但实际情况不是这样，分别输出实际情况的花费和 \(DLee\) 认为的花费。
思路：
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
void solve(){
LL n;
cin >> n;
vector <LL> a(n);
for (int i = 0; i < n; i ++ ){
cin >> a[i];
}
LL sum = 0;
double c1 = 0, c2 = 0;
for (int i = 0; i < n; i ++ ){
if (c2 >= 200){
c2 += a[i] * 0.5;
}
else if (c2 >= 100){
c2 += a[i] * 0.8;
}
else{
c2 += a[i];
}
sum += a[i];
}
if (sum < 100){
c1 = sum;
}
else if (sum < 225){
c1 = 100 + (sum - 100) * 0.8;
}
else {
c1 = 200 + (sum - 225) * 0.5;
}
cout << fixed << setprecision(3) << c1 << " " << c2 << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
G - Climb Stairs
题意：
有 \(n\) 层关卡，每关有一个怪物，生命值为 \(a_i\)，初始角色的攻击力为 \(a_0\)，刚开始在第 0 层，当攻击力大于怪物生命值时，可以击败怪物，同时攻击力会增加 \(a_i\) 点，每次可以选择到当前层上面第 1,2,...,\(k\) 层，或者向下走一层，已走过的层不能走。
思路：
假设从第 \(x\) 层向上到第 \(y\) 层，那么接下来必须将 \([x + 1, y - 1]\) 层的怪物都击败，然后再向上。
设能从第 \(i\) 层打到第 \([x + 1]\) 层的攻击力为 \(mx\)，\(mx = max(mx - a[i], a[i])\)（打败它上一层的怪物下来或者从这个怪物开始打然后往下走）。
如果当前攻击力大于这个值，根据贪心的思路，就从这一层开始打，因为这样打的话，越往后，自己的攻击力就越大，那么打败后面的怪物的可能性就越大。
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
void solve(){
LL n, ap, k;
cin >> n >> ap >> k;
vector <LL> a(n + 1);
for (int i = 1; i <= n; i ++ )
cin >> a[i];
LL cur = 0, t = k;
while(1){
LL mx = 0;
bool ok = false;
for (int i = cur + 1; i <= min(cur + k, n); i ++ ){
mx = max(mx - a[i], a[i]);
if (mx <= ap){
ok = true;
for (int j = i; j > cur; j -- )
ap += a[j];
k = t - (i - cur) + 1;
cur = i;
}
}
if (!ok){
cout << "NO\n";
return;
}
if (cur == n){
cout << "YES\n";
return;
}
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T = 1;
cin >> T;
while(T -- ){
solve();
}
return 0;
}
