比赛链接：
https://atcoder.jp/contests/abc253
F - Operations on a Matrix
题意：
\(n * m\) 的初始值全为 0 的矩阵，\(q\) 次询问，有三种操作。
操作 1：l 到 \(r\) 所有列的所有元素都加上 \(x\)。
操作 2：将第 \(i\) 列所有元素都替换成 \(x\)。
操作 3：查询 \((i, j)\) 的元素值。
思路：
行列分开来考虑，对于列，可以通过树状数组维护一个差分数组去计算。
对于行，对这个位置有影响的只有最近的一次操作 2，每次将最近的一次操作 2 记录下来，然后查询的时候进行修改。
查询的位置的答案就是改行最近一次操作 2 的赋值 + 在这次操作之后所有对该位置有影响的操作 1 的值。
\(ans_{i,j} = r + s_j - s_r\)
\(ans_{i,j}\) 就是最后的答案。
\(r\) 是查询的这一行最近的一次操作 2。
\(s_j\) 表示到当前这一步所有操作的第 \(i\) 列的值。
\(s_r\) 表示到查询的这一行最近的一次操作 2 的所有操作的第 \(i\) 列的值。
可以考虑每一个操作 2 对后面查询值的影响，在读入时记录下每个操作 2 的影响，然后再通过一个树状数组去求最终的答案。
即先求出 \(r + s_j\) 然后再逐个减去 \(s_r\)。
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
struct fwt{
LL n;
vector <LL> a;
fwt(LL n) : n(n), a(n + 1) {}
LL sum(LL x){
LL res = 0;
for (; x; x -= x & -x)
res += a[x];
return res;
}
void add(LL x, LL k){
for (; x <= n; x += x & -x)
a[x] += k;
}
LL query(LL x, LL y){
return sum(y) - sum(x - 1);
}
};
LL n, m, q;
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cin >> n >> m >> q;
vector <LL> op(q), l(q), r(q), x(q), ans(q);
vector < vector < pair < LL, LL> > > sub(q);
vector < pair < LL, LL> > last(n + 1);
fwt f(m);
for (int i = 0; i < q; i ++ ){
cin >> op[i];
if (op[i] == 1){
cin >> l[i] >> r[i] >> x[i];
f.add(l[i], x[i]);
f.add(r[i] + 1, -x[i]);
}
else if (op[i] == 2){
cin >> r[i] >> x[i];
last[r[i]] = {i, x[i]};
}
else{
cin >> l[i] >> r[i];
auto [p, num] = last[l[i]];
ans[i] = num + f.sum(r[i]);
sub[p].push_back({i, r[i]});
}
}
fwt t(m);
for (int i = 0; i < q; i ++ ){
for (auto [p, c] : sub[i])
ans[p] -= t.sum(c);
if (op[i] == 1){
t.add(l[i], x[i]);
t.add(r[i] + 1, -x[i]);
}
if (op[i] == 3)
cout << ans[i] << "\n";
}
return 0;
}
G - Swap Many Times
题意：
将 \(\frac{n(n - 1)}{2}\) 个数对 \((x, y)\) 按照升序排序，其中 1 \(\le x < y \le n\)。
依次选择第 \(L\) 位到第 \(R\) 位的数对，对序列 \(A = {1, 2,..., N}\) 进行操作。记选择的数对为 \((x, y)\)，交换 \(A_x\) 和 \(A_y\)，问最后的序列 \(A\) 为什么。
思路：
将数对按照如下方式排列
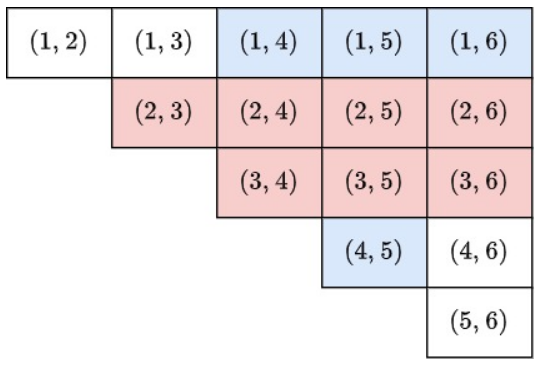
对第 \(i\) 行整行的数对进行操作后等价于将序列第 \(i\) 位到最后的区间整体向后移动一位，最后一位移到前面。
例如序列 1, 2..., 6，依次操作 (2, 3), (2, 4),..., (2, 6)，序列变成 1, 6, 2, 3.., 5。
所以对于 \(L\) 到 \(R\) 的区间，可以分开来，除去 \(L\) 和 \(R\) 所在行，都进行翻转，然后这两行暴力交换即可。
代码：
#include<bits/stdc++.h>
using namespace std;
using LL = long long;
int main(){
LL n, L, R;
cin >> n >> L >> R;
LL sum = 0;
int st;
for (int i = 1; i <= n; i ++ ){
sum += n - i;
if (sum >= L){
st = i;
L = L - sum + n - i;
break;
}
}
sum = 0;
int ed;
for (int i = 1; i <= n; i ++ ){
sum += n - i;
if (sum >= R){
ed = i;
R = R - sum + n - i;
break;
}
}
vector<int> a(n + 1);
iota(a.begin(), a.end(), 0);
if (st == ed){
for (int i = L; i <= R; i ++ ){
swap(a[st], a[i + st]);
}
}
else{
for (int i = L + st; i <= n; i ++ ){
swap(a[st], a[i]);
}
if (st + 1 <= ed - 1){
reverse(a.begin() + st + 1, a.end());
reverse(a.begin() + ed, a.end());
}
for (int i = ed + 1; i <= ed + R; i ++ ){
swap(a[ed], a[i]);
}
}
for (int i = 1; i <= n; i ++ ){
cout << a[i] << " \n"[i == n];
}
return 0;
}
