比赛总结:
第一次现场省赛,赛前是期望银的,最后三分钟才过了第七题,最后捡个铜。
这场比赛我背大锅,赛前一段时间的状态不太稳定,比赛的时候先是开的第六题用 manacher 去算每个字符为中心的最长的字符串的时候错了,那时候过了一个测试就没想着多测几组,最后浪费了队友一个小时。后来在开的第七题上面先是理解错题目,然后又固执地坚持自己的做法又 debug 不出问题,最后卡了俩小时。
开场四十分钟时候过了四题的时候,在预期之内,第一题题意说实话有点小问题,所以尝试了两个方法,wa 了一次。
接下来就是罚坐了,最短路那一道题写了一个多小时,然后剩下的两道题都在最后半小时极限过掉。
比赛也暴露了很多缺点:一个是代码的实现能力和 debug,最短路实现了一个多小时,大模拟水题 debug 两个小时;接着是知识点的覆盖,manacher 只有一个人懂;最后是配合的问题,互相之间的代码不太想看(可能每个人都不太想看其他人的代码),占着电脑有时候其实思路越来越乱,还不如让其他人重构。
比赛链接:
https://codeforces.com/gym/103687
补题:
A. JB Loves Math
题意:
给定一个两个数 \(a\) 和 \(b\),可以选择一个奇数 \(x\) 和一个偶数 \(y\),选定后无法改变(比赛的时候好像是没有这句话的),每一操作可以让 \(a\) 加上 \(x\) 或者 \(a\) 减去 \(y\),问将 \(a\) 变成 \(b\) 最少需要几步操作。
思路:
每一类讨论一下就行。
当 \(a\) 等于 \(b\) 时,0 步。
当 \(a\) > \(b\) 时,
如果它们之间差偶数,减去一个偶数就行。
如果差奇数,那两步,加上一个奇数,减去一个偶数。
当 \(a\) < \(b\) 时,
如果它们之间差奇数,加上一个奇数就行。
如果差偶数,还要分两类,如果偶数可以分成两个奇数,那么加上两个奇数就行,不然要减去一个偶数后再加上两个奇数。
代码:
#include<bits/stdc++.h>
using namespace std;
int T = 1, a, b;
void solve(){
cin >> a >> b;
if (a == b) cout << "0\n";
else if (a > b){
if ( (a - b) % 2 == 0 ) cout << "1\n";
else cout << "2\n";
}
else {
if ( (b - a) & 1 ) cout << "1\n";
else {
int t = (b - a) / 2;
if (t & 1) cout << "2\n";
else cout << "3\n";
}
}
}
int main() {
ios::sync_with_stdio(false);cin.tie(0);
cin >> T;
while(T--)
solve();
return 0;
}
B. JB Loves Comma
题意:
给定一个字符串,在每一个 "cjb" 子串后面加入一个逗号。
思路:
按题意计算。
代码:
#include <bits/stdc++.h>
using namespace std;
string s;
int main(){
cin >> s;
for (int i = 0; i < s.size() - 2; i ++ ){
if (s.substr(i, 3) == "cjb"){
s.insert(s.begin() + i + 3, ',');
}
}
cout << s << "\n";
return 0;
}
C. JB Wants to Earn Big Money
题意:
\(n\) 个人想要买股份,\(m\) 个人想要出售股份,给出每个人想买的股份的价格和想出售的股份的价格,最后的定价为 \(x\)。
当想买的人的价格大于等于 \(x\) 时,它会加入交易,当想出售的人的价格小于等于 \(x\) 时,它会加入交易,问最后有多少个人加入交易。
思想:
按照题意计算就行。
代码:
#include <bits/stdc++.h>
using namespace std;
int n, m, x, a, b, ans;
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cin >> n >> m >> x;
for (int i = 1; i <= n; i ++ ){
cin >> a;
if (a >= x)
ans ++ ;
}
for (int i = 1; i <= m; i ++ ){
cin >> b;
if (b <= x)
ans ++ ;
}
cout << ans << "\n";
return 0;
}
G. Easy Glide
题意:
从点 \(s\) 出发到点 \(t\),以 v1 的速度开始运动,中间有 \(n\) 个点加速点,到达加速点之后的 3 秒会以 \(v2\) 的速度运动,然后又变回 \(v1\),问从 \(s\) 到 \(t\) 的最短时间是多少。
思路:
显然,从起点出发后,肯定去终点或者去加速点,所以构建起点到所有终点和加速点的边。
在某个加速点,会去另一个加速点或者去终点,所以构建每个加速点到其它加速点和终点的边。
然后通过最短路算法计算就行。
代码:
#include<bits/stdc++.h>
using namespace std;
#define PDI pair <double, int>
#define fi first
#define se second
const int N = 1e3 + 10, M = 2e6 + 10;
int n, v[N];
double x[N], y[N], v1, v2, dis[N];
vector < PDI > g[M];
double calT1(int a, int b){
double dx = x[a] - x[b], dy = y[a] - y[b];
double d = sqrt(dx * dx + dy * dy);
return d / v1;
}
double calT2(int a, int b){
double dx = x[a] - x[b], dy = y[a] - y[b];
double d = sqrt( dx * dx + dy * dy );
if (d <= 3 * v2) return d / v2;
else return (d - v2 * 3) / v1 + 3;
}
void dijkstra(){
for (int i = 1; i <= n + 1; i ++ )
dis[i] = 1e7;
dis[0] = 0;
priority_queue< PDI, vector<PDI>, greater<PDI> > q;
q.push( {0, 0} );
while ( q.size() ){
PDI t = q.top();
q.pop();
int x = t.se;
if (v[x]) continue;
v[x] = 1;
for (auto tt : g[x]){
double d = tt.fi;
int y = tt.se;
if (dis[y] > dis[x] + d){
dis[y] = dis[x] + d;
q.push( { dis[y], y} );
}
}
}
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++ )
cin >> x[i] >> y[i];
cin >> x[0] >> y[0] >> x[n + 1] >> y[n + 1];
cin >> v1 >> v2;
for (int i = 1; i <= n + 1; i ++ )
g[0].push_back({calT1(0, i), i});
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n + 1; j ++ )
g[i].push_back({calT2(i, j), j});
dijkstra();
printf("%.12lf\n", dis[n + 1]);
return 0;
}
I. Barbecue
题意:
长为 \(n\) 的字符串,\(q\) 次询问,每次选择一段区间 \(l\) 到 \(r\),\(Putata\) 和 \(Budada\) 轮流在字符串上博弈,每次可以删除选中字符串的开头字符或者结尾字符,当有人拿到的是回文的字符时,就输了。每次询问判断谁获胜。
思路:
首先判断初始的字符串是不是回文的,通过 \(manacher\) 或者 \(hash\) 判断,是的话 \(Putata\) 直接就输了。
如果不是,因为采取最优的策略,肯定不会让自己得到回文字符串,所以最后只可能是剩下一个字符的时候。判断一下选中字符串的奇偶性即可。
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
char s[N << 1];
int p[N << 1], n, q;
string ss;
void manacher(){
s[0] = '-', s[1] = '#';
for (int i = 0; i < n; i ++ ){
s[2 * i + 2] = ss[i];
s[2 * i + 3] = '#';
}
n = n * 2 + 1;
s[n + 1] = '+';
int mid = 0, r = 0;
for (int i = 1; i < n; i ++ ){
if (i < r) p[i] = min(p[(mid << 1) - i], r - i);
else p[i] = 1;
while(s[i - p[i]] == s[i + p[i]]) p[i]++;
if (i + p[i] > r){
r = i + p[i];
mid = i;
}
}
}
int main() {
ios::sync_with_stdio(false); cin.tie(0);
cin >> n >> q;
cin >> ss;
manacher();
for (int i = 1; i <= q; ++ i) {
int x, y;
cin >> x >> y;
int xx = x, yy = y;
x *= 2, y *= 2;
int mid = (x + y) / 2;
if ( 2 * p[mid] - 1 >= y - x + 1 ) cout << "Budada\n";
else {
if ( (yy - xx + 1) % 2 == 0 ) cout << "Budada\n";
else cout << "Putata\n";
}
}
return 0;
}
J. Frog
题意:
有一个圆心在(0,0)的半径为 1 的圆柱,有一只青蛙在圆柱的边缘,它每次可以跳到离当前位置距离为 1 的地方,问青蛙从指定的起点跳到指定的终点最少多少步,同时输出每次的落脚点坐标。注意,青蛙在任何时刻都不能进入圆柱的范围。
思路:
为了方便操作,思考的时候将起点移动到(1,0)。
接着考虑两个特殊的点,(0,1)和(-1,0),青蛙到(0,1)最少两步,这也是它两步能到的最远的距离,到(-1,0)最少四步,这也是青蛙四步能到的最远的距离。
然后看三步能到的最远的情况在哪。容易知道如果青蛙在圆柱边缘,它能到的最远的地方的运动轨迹一定和起跳位置相切的。所以三步最远的位置如下。
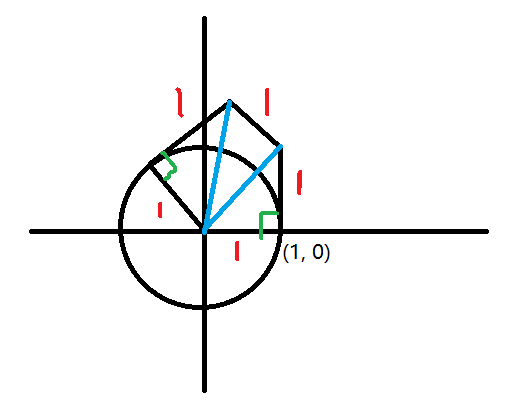
可以得到蓝色直线的夹角的 \(cos\) 值为 \(\frac{3}{4}\),大约 41° 左右。
所以总共四种情况。
1.起点和终点重合,0 步。
2.起点和终点的夹角 <= 90°,两步。
可以以圆心为参考,起点出发先到圆心,再到终点。因为不能进入圆柱范围。所以将圆心按照起点和终点的连线对称出去,将对称点作为中转点。
3.起点和终点的夹角 <= 131°,三步。
参照下图。
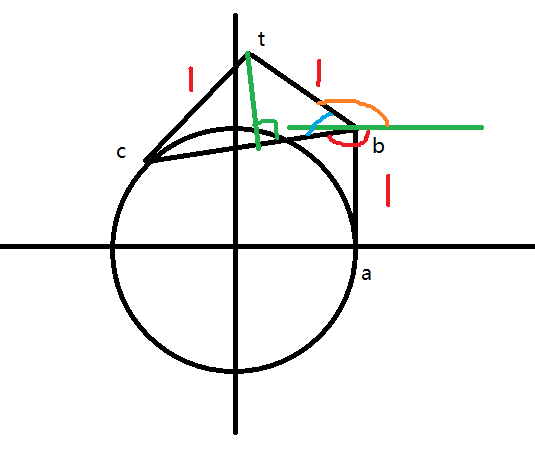
\(a\) 为起点,\(b\),\(t\) 为中转点,\(c\) 为终点。
参考 jiangly 的代码得出的思路。
先从起点向最远的位置移动一步,即走与半径相切的路径,到达 \(b\) 点。
现在希望知道橙色的角,从而求 \(t\) 的坐标,因为橙色的角 + 红色的角 + 蓝色的角的和为 360°,所以考虑求红色的角和蓝色的角。
通过求线段 \(bc\) 的长度,可以求蓝色的角的余弦值,从而求蓝色的角,再通过 \(b\) 和 \(c\) 的坐标,可以求得红色的角的正切值,从而求红色的角。
这样子就求出了所有的点的坐标。
4.起点和终点的夹角 <= 180°,四步。
先花两步到达(0,1),剩下两步就和第一种情况一样了。
当起点和终点的角度 > 180° 的时候,只需要翻转一下输出即可。
代码:
#include <bits/stdc++.h>
using namespace std;
const double Pi = acos(-1);
array<double, 2> get(int x){ //返回该角度对应的坐标
double t = x * Pi / 180;
return {cos(t), sin(t)};
}
void solve(){
int s, t;
cin >> s >> t;
int d = (t - s + 360) % 360;
bool rev = false;
vector < array <double, 2> > ans;
if (d > 180){
rev = true;
swap(s, t);
d = 360 - d;
}
auto a = get(s), b = get(s + 90), c = get(t);
if (d == 0){
ans.push_back(a);
}
else if (d <= 90){
ans.push_back(a);
ans.push_back({a[0] + c[0], a[1] + c[1]});
ans.push_back(c);
}
else if (d <= 131){
b[0] += a[0];
b[1] += a[1];
double dis = sqrt( (b[0] - c[0]) * (b[0] - c[0]) + (b[1] - c[1]) * (b[1] - c[1]) );
double x = atan2(c[1] - b[1], c[0] - b[0]) - acos(dis / 2);
ans.push_back(a);
ans.push_back(b);
ans.push_back({b[0] + cos(x), b[1] + sin(x)});
ans.push_back(c);
}
else{
ans.push_back(a);
ans.push_back({a[0] + b[0], a[1] + b[1]});
ans.push_back(b);
ans.push_back({b[0] + c[0], b[1] + c[1]});
ans.push_back(c);
}
if (rev) reverse(ans.begin(), ans.end());
cout << ans.size() - 1 << "\n";
for (auto [x, y] : ans)
cout << x << " " << y << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cout << fixed << setprecision(10);
int T;
cin >> T;
while(T -- )
solve();
return 0;
}
L. Candy Machine
题意:
给定 \(n\) 个数,选择一个子集,问让子集中严格大于子集平均数的数最多有多少。
思路:
贪心的思想,为了让平均值最小,那么一定选中了最小的几个,先排个序。答案一定是某个前缀的值,通过双指针或者二分求解。
代码:
#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL n, s, ans;
int main() {
ios::sync_with_stdio(false);cin.tie(0);
cin >> n;
vector <LL> a(n + 1);
for (int i = 1; i <= n; i ++ )
cin >> a[i];
sort(a.begin() + 1, a.end());
for (LL l = 1, r = 1; r <= n; r ++ ){
s += a[r];
while (l < r && a[l] * r <= s) l ++ ;
ans = max(ans, r - l + 1);
}
cout << ans << "\n";
return 0;
}
M. BpbBppbpBB
题意:
将 \(C\) 和 \(S\) 两种类型的图形不重叠地放到一个矩阵中。
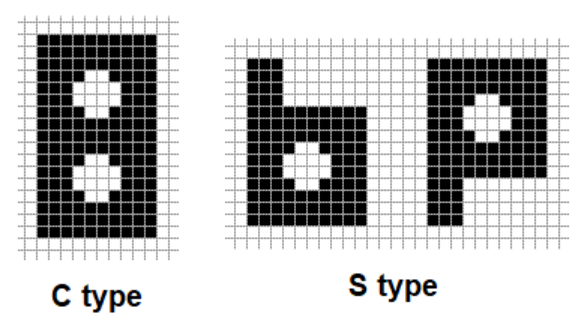
已知放好之后的矩阵,求出每个图形放了多少个,图形可能旋转了 90 度的倍数之后放置进去的。
思路:
因为没有重叠,可以先找到中间的白块,然后判断一下这个白块是 \(C\) 的还是 \(S\) 的,直接模拟求解即可。
比赛的时候 \(if\) 忘了 \(else\),卡了俩小时,虽然 a 了,但是,以后不想模拟了。
因为每个图形黑方块的数量和中间白色块的数量是固定的,所以考虑推数学公式。
设有 \(x\) 个 \(C\),\(y\) 个 \(S\),记 \(sumb\) 为黑方块的数量,\(cntw\) 为中间白色块的数量。
得到方程:
\(146 * x + 100 * y = sumb\)
\(2 * x + y = cntw\)
推出 \(x = \frac{100 * cntw - sumb}{54}, y = cntw - 2 * x\)。
在判断中间白块的时候,起码要判断 6 * 6 的,4 * 4 的会被卡。因为四个角的黑块都属于一个图形的时候,这个位置的白块其实不需要被记录。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int n, m, cntw, sumb;
char a[N][N];
vector <string> t = {
"######",
"##..##",
"#....#",
"#....#",
"##..##",
"######"
};
int check(int x, int y){
for (int i = 0; i <= 5; i ++ )
for (int j = 0; j <= 5; j ++ )
if (x < 1 || y < 1 || x + i > n || y + j > m || a[x + i][y + j] != t[i][j])
return 0;
return 1;
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
cin >> a[i][j];
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
if (a[i][j] == '#') sumb ++ ;
else cntw += check(i - 1, j - 2);
int x = (cntw * 100 - sumb) / 54;
cout << x << " " << cntw - 2 * x << "\n";
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号