比赛链接:
https://ac.nowcoder.com/acm/contest/11223
D.生活在树上
题目大意:
\(n\) 个点,\(n - 1\) 条带权边的树,每次只能从一个节点移动不超过两个单位的距离,分别求出从每一个点出发,能到达多少个点。
思路:
从一个点最多移动两个距离,因为权是 >= 1 的,所以只有两种情况,一种是移动到邻近的边权为 2 的点,另一种是移动到邻近的边权为 1 的点,然后移动到另一个边权为 1 的点。
先记录每一个节点边权为 1 及 2 的点的数量,接着考虑移动到边权为 1 的点后的移动方案。
设从 \(u\) 点移动到了 \(v\),且 \((u, v) = 1\)。那么从 \(v\) 移动到邻近的一个点的方案数就是 \(v\) 点边权为 1 的点的数量 - 1(因为不能移回 \(u\))。
答案就是边权为 1 的点的数量 + 边权为 2 的点的数量 + 移动到边权为 1 的点后再移动到边权为 1 的点的数量 + 1(自己)。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
#define LL long long
LL n, cnt[N][2], ans[N];
vector < pair< LL, LL> > g[N];
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cin >> n;
for (LL u = 2; u <= n; ++ u){
LL v, w;
cin >> v >> w;
g[u].push_back( {w, v});
g[v].push_back( {w, u});
}
for (LL u = 1; u <= n; ++ u)
for (auto [d, v] : g[u])
if (d == 1) cnt[u][0]++;
else if (d == 2) cnt[u][1]++;
for (LL u = 1; u <= n; ++ u)
for (auto [d, v] : g[u])
if (d == 1) ans[u] += cnt[v][0] - 1;
for (LL i = 1; i <= n; ++ i)
cout << ans[i] + cnt[i][0] + cnt[i][1] + 1 << "\n";
return 0;
}
E.对决
题目大意:
\(n\) 个人进行比赛,每个人的能力值为 \(a_i\),现在进行 \(n - 1\) 次比赛,通过改变比赛的顺序,依次判断每个人是否成为冠军。
\(i\) 和 \(j\) 比赛,当 \(a_i >= a_j\) 时,都算获胜。
整个比赛中能使用两个道具来帮助某个人夺冠,每个只能使用一次,可以在同一场比赛中一起使用,一个道具可以让一个人在这场比赛中的能力值 *2,另一个道具可以让对手在这场比赛中的能力值 /2。
冠军需要至少进行 \(k\) 场比赛。
思路:
首先进行一个排序,对于每个人,不用道具的情况下,可以战胜所有小于等于自己的对手。
若该数量大于等于 \(k\),那么自己只需要通过两个道具战胜能力值最大的敌人即可。
还有一种特殊情况,即自己的能力值为 \(x\),通过 /2 道具战胜一个能力值比自己大的人,这个人的能力值最大可以为 \(2*x + 1\),这个人再通过一个道具战胜能力值最大的那个人,最大的那个人的能力值为 \(4*x + 2\)。这种方式比直接用两个道具和能力值最大值的那个人比赛更优。
若该数量等于 \(k - 1\) 的时候,至少需要再打两场,能力值最大的人肯定通过一个道具战胜,另一个对手,应该选择能力值比自己大的所有人里面能力值最小的那个人,通过一个道具战胜,那么就可以夺冠了。
找到能力值比自己大的那个人可以通过二分,也可以通过找与自己相同的,那么接下的一个就是比自己大的了。
代码:
二分查找
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define fi first
#define se second
const LL INF = 1e9 + 1;
LL n, k;
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cin >> n >> k;
vector <LL> ans(n + 1);
vector < pair <LL, LL> > a(n + 1);
set <LL> s;
for (LL i = 1; i <= n; ++ i){
cin >> a[i].fi;
a[i].se = i;
s.insert(a[i].fi);
}
sort( a.begin() + 1, a.begin() + n + 1 );
for (int i = 1; i <= n; ++ i){
LL p = upper_bound( a.begin() + 1, a.begin() + n + 1, make_pair( a[i].fi, INF ) ) - a.begin();
if ( p > n ) ans[a[i].se] = 1;
else if ( p >= k + 1 && ( ( a[i].fi * 2 >= a[n].fi / 2 ) || ( s.count( a[i].fi * 2 + 1 ) && a[i].fi * 4 + 2 == a[n].fi ) ) ) ans[a[i].se] = 1;
else if ( p == k && a[i].fi * 2 >= a[p].fi && a[i].fi >= a[n].fi / 2 ) ans[a[i].se] = 1;
}
for (int i = 1; i <= n; ++ i)
cout << ans[i] << " \n"[i == n];
return 0;
}
找到所有相同的
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define fi first
#define se second
LL n, k;
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cin >> n >> k;
vector <LL> ans(n + 1);
vector < pair <LL, LL> > a(n + 1);
set <LL> s;
for (LL i = 1; i <= n; ++ i){
cin >> a[i].fi;
a[i].se = i;
s.insert(a[i].fi);
}
sort( a.begin() + 1, a.begin() + n + 1 );
for (LL i = 1; i <= n; ++ i){
LL p = i + 1;
while ( a[i].fi == a[p].fi && p <= n ) p++;
p--;
for (int j = i; j <= p; ++ j){
bool f = false;
if ( p == n ) f = true;
if ( p >= k && ( a[p].fi * 2 >= a[n].fi / 2 || ( s.count( a[p].fi * 2 + 1 ) && a[p].fi * 4 + 2 == a[n].fi ) ) ) f = true;
if ( p == k - 1 && a[p].fi * 2 >= a[p + 1].fi && a[p].fi >= a[n].fi / 2 ) f = true;
if ( f ) ans[a[j].se] = 1;
}
i = p;
}
for (int i = 1; i <= n; ++ i)
cout << ans[i] << " \n"[i == n];
return 0;
}
F.数对
题目大意:
给定 \(n\) 和 \(k\),求出有多少个整数对 \((v, u)\) 满足 \(1 <= v < u <= n\) 且 \(k <= u + v\),\(k <= u * v\)。
思路:
将条件整理一下,变成
\(1 <= v <= n\)
\(1 <= u <= n\)
\(v + 1 <= u\)
\(k <= v * u\)
问题就变成了求出多少个整数点落在这个区域内。线性规划的题目。
因为 \(k\) 的不同,可以分成四种情况。
1:
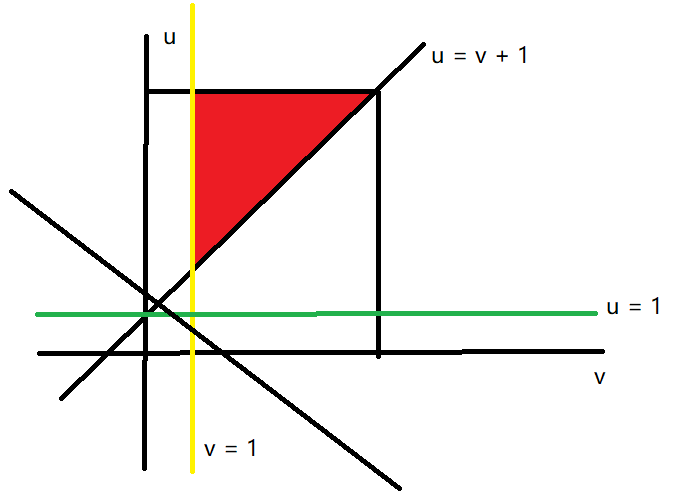
答案就是红色区域中整数点的数量。等差数列求和即可。
2:
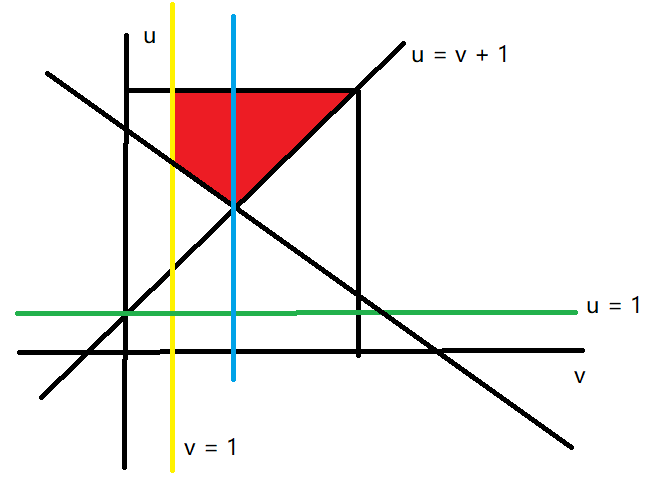
可以将要求的四边形用图中的蓝色线分成两块来计算。
左边和右边的部分分别等差数列求和,这样子的话要考虑 \(u + v = k\) 和 \(u = v + 1\) 这两条直线的交点坐标是不是整数点。
接着要减去 1,因为左下角 \((1, k - 1)\) 这个点不符合限制条件。
3:
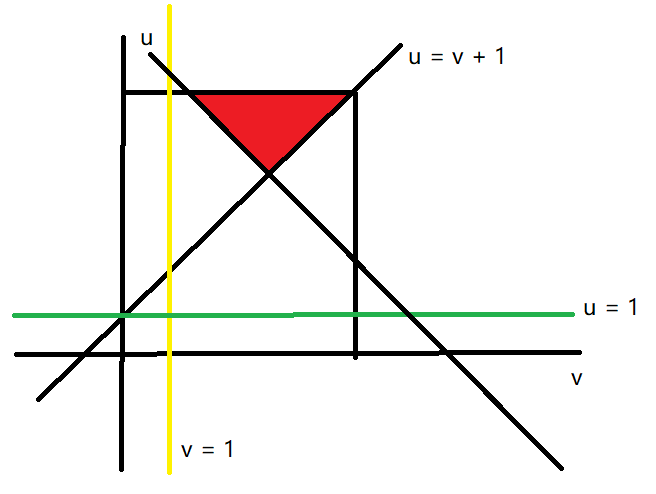
可以按照第二类分成两块来计算。
4:
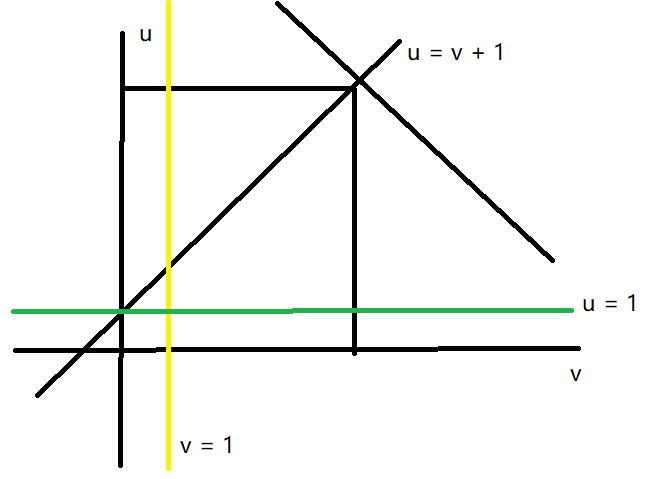
没有点满足条件。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
void solve(){
LL ans = 0, n, k;
cin >> n >> k;
LL x = (k - 1) / 2, y = (k + 1) / 2;
if (k % 2 == 0) y++;
if (k <= 2) ans = n * (n - 1) / 2;
else if (k <= n + 1){
if (k & 1) ans = (n - (k - 1) + 1 + n - y + 1) * x / 2 + (1 + n - y + 1) * (n - x) / 2 - (n - y + 1);
else ans = (n - (k - 1) + 1 + n - y + 1) * x / 2 + (1 + n - y + 1) * (n - 1 - x) / 2;
ans--;
}
else if (k <= 2 * n - 1){
if (k & 1) ans = (1 + n - y + 1) * (n - (k - n) + 1) / 2 - (n - y + 1);
else ans = (1 + n - y + 1) * (n - (k - n)) / 2;
}
cout << ans << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
LL T;
cin >> T;
while (T--)
solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号