比赛链接:
https://ac.nowcoder.com/acm/contest/11186
A.小y的平面
思路:
因为只能向右或者向上走,所以能走的下一个点只能在右上。
依据 x + y 的值对点进行一个排序(我没排序也过了,测试点好像有点水),然后循环判断就可以了。
代码:
#include <bits/stdc++.h>
using namespace std;
#define all(x) (x).begin(), (x).end()
#define fi first
#define LL long long
#define pb push_back
#define PII pair <int, int>
#define se second
const int N = 1e6 + 10, M = 2e5 + 10;
const int mod = 1e9 + 7;
LL T = 1, n;
string s;
struct node{
int x, y;
}p[N];
bool cmp(node a, node b){
return a.x + a.y < b.x + b.y;
}
void solve(){
cin >> n;
for (int i = 1; i <= n; i++)
scanf("%d%d", &p[i].x, &p[i].y);
sort(p + 1, p + n + 1, cmp);
for (int i = 2; i <= n; i++)
if (p[i].x < p[i - 1].x || p[i].y < p[i - 1].y){
cout << "NO\n";
return;
}
cout << "YES\n";
}
int main(){
// cin >> T;
while(T--)
solve();
return 0;
}
B.小y的树
思路:
定义根节点为树的第 0 层,其子节点为第 1 层,那么这颗树总共有 \(n - 1\) 层,我们一层一层考虑。
根节点(即第 0 层)到所有节点的距离很好求,可以算出来是 \(\sum_{i = 0}^{n - 1} i * k^i\)。
接下来我们考虑第 1 层的一个节点到其它子节点的距离。
若设 \(t\) 为第 0 层节点到其它所有节点的距离和,而第 1 层的节点相比于第 0 层的节点,到 \(a\) 部分节点的距离减少了 1,到 \(b\) 部分节点的距离增加了 1,总距离的变化就是 \(a - b\)。
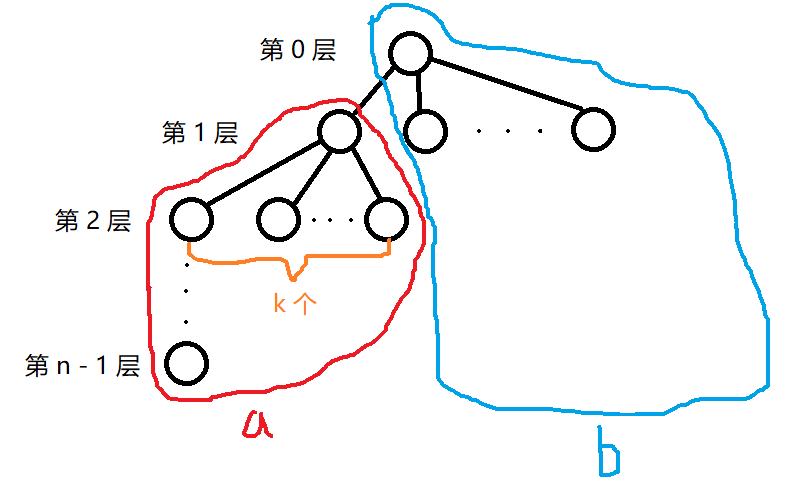
\(a\) 就是一个子树的总点数,可以通过循环去求解,那么 \(b\) 就是树的总点数减去 \(a\)。
这样子求出来了每个点到其他点的总距离之和,但是每条边我们计算了两次,所以最后结果要除 2,这里就要用到逆元,因为要先除后取模。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e6 + 10;
const int mod = 1e9 + 7;
LL T = 1, n, ans, k, sum, t, s[N];
LL qpow(LL a, LL b){
if (b == 0) return 1;
LL ans = 1;
while (b != 0){
if (b & 1) ans = (ans * a) % mod;
b >>= 1;
a = (a * a) % mod;
}
return ans;
}
LL inv(LL x, LL p){//逆元
return qpow(x, p - 2);
}
void solve(){
cin >> n >> k;
//sum 为点数的总和, t 为当前层的值
for (LL i = 0; i <= n - 1; i++){
LL l = qpow(k, i);
t = (t + (i * l) % mod) % mod;
sum = (sum + l) % mod;
s[i] = sum;
}
ans = t;
for (LL i = 2; i <= n; i++){
LL l = qpow(k, i - 1);
t = (t + (sum - (s[n - i] * 2) % mod + mod) % mod) % mod;
ans = (ans + (l * t % mod) % mod) % mod;
}
cout << (ans * inv(2, mod)) % mod << "\n";
}
int main(){
// cin >> T;
while(T--)
solve();
return 0;
}
C.小y的序列
题目大意:
定义一个区间 \([l, r]\) 的美丽值为 \(max(a[i], ..., a[j]) = min(a[i], ..., a[j]) + k (l <= i <= j <= r)\) 的个数。
给定一个长为 \(n\) 的序列以及 \(k\),求出 \([1, n]\) 的美丽值。
思路:
如果固定了左端点,随着右端点的右移,区间最大值减去区间最小值的结果非递减,所以固定左端点,然后二分查找右端点。
先二分找到最大值减去最小值等于 \(k\) 的左端点,判断是否符合条件,若是,再找右端点,计算答案。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e6 + 10;
int n, k, mx[N][21], mn[N][21], a[N];
LL ans;
void init(){
for (int i = 1; i <= n; i ++ ){
mx[i][0] = a[i];
mn[i][0] = a[i];
}
int k = log2(n);
for (int j = 1; j <= k; j ++ )
for (int i = 1; i + (1 << j) - 1 <= n; i ++ ){
mx[i][j] = max(mx[i][j - 1], mx[i + ( 1 << (j - 1) )][j - 1]);
mn[i][j] = min(mn[i][j - 1], mn[i + ( 1 << (j - 1) )][j - 1]);
}
}
int query(int l, int r){
int k = log2(r - l + 1);
return max(mx[l][k], mx[r - (1 << k) + 1][k]) - min(mn[l][k], mn[r - (1 << k) + 1][k]);
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
cin >> n >> k;
for (int i = 1; i <= n; i ++ )
cin >> a[i];
init();
for (int i = 1; i <= n; i ++ ){
int l = i, r = n;
while (l < r){
int mid = l + r >> 1;
if (query(i, mid) < k) l = mid + 1;
else r = mid;
}
int p = l;
if (query(i, p) < k) continue;
l = i, r = n;
while (l < r){
int mid = l + r + 1 >> 1;
if (query(i, mid) <= k) l = mid;
else r = mid - 1;
}
int q = l;
ans += q - p + 1;
}
cout << ans << "\n";
return 0;
}
D.小y的质因数
题目大意:
\(T\) 组询问,每次给出三个数 \(l, r, k\),代表询问在区间 \([l, r]\) 之间的数 \(x\) 满足 \(x\) 的质因子个数大于等于 \(log2(x) - k\) 的个数。
思路:
因为 \(l\) 和 \(r\) 的数据范围小于 \(1e12\),同时 \(k\) 最大为 10。在 \(1e12\) 中质因子个数大于等于 \(log2(x) - k\) 的数是有限的。暴力搜出每一个 \(k\) 对应的数,然后二分查找。
在 \(dfs\) 中,只需要搜索到 \(log2(x)\) - 质因子个数等于 10 的就可以停止了,不然就 \(T\) 了。
这样子,最小的质因子就可以求出来了。\(log2(1e12)\) 是 40,差为 10,所以将 11 个 2 合并,即 \(2^{11}\),其它质因子都是 2,可以得到要搜的最大的质因数为 2048,用质数筛预处理一下。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e6 + 10;
LL T, l, r, k;
int prime[N], cnt;
bool st[N];
vector <LL> num[11];
void get_primes(int n){
st[1] = true;
for (int i = 2; i <= n; i ++ ){
if (!st[i]) prime[++ cnt] = i;
for (int j = 1; j <= cnt && i * prime[j] <= n; j ++ ){
st[i * prime[j]] = true;
if (i % prime[j] == 0) break;
}
}
}
void dfs(LL x, LL y, LL p){
if (p < (LL)ceil(log2(x)) - 10) return;
if (y == cnt + 1){
num[(LL)ceil(log2(x)) - p].push_back(x);
return;
}
for (int i = 0; x <= 1e12; ++ i){
dfs(x, y + 1, p + i);
x *= prime[y];
}
}
void init(){
get_primes(2100);
dfs(1, 1, 0);
for (int i = 0; i <= 10; i ++ )
sort(num[i].begin(), num[i].end());
}
void solve(){
cin >> l >> r >> k;
LL ans = 0;
for (int i = 0; i <= k; i ++ )
ans += upper_bound(num[i].begin(), num[i].end(), r) - lower_bound(num[i].begin(), num[i].end(), l);
cout << ans << "\n";
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);
init();
cin >> T;
while ( T -- )
solve();
return 0;
}
E.小y的容器
题意:
将 \(n\) 个数放到三个容器中,有 \(m\) 个限制,每个限制告诉你 \(x\) 不能放到 \(y\) 容器中,求出每个容器中的数进行排序后相邻两个数之间的差值 <= 3 的放置数字的方案数(每个容器中至少有一个数字)。
思想:
容易想到定义 \(dp[i][a][b][c]\) 为将第 \(i\) 个数放到容器后,第一个容器中最后一个数为 \(a\),第二个容器中最后一个数为 \(b\),第三个容器中最后一个数为 \(c\)。
但是这个 \(dp\) 方程的空间大小为 \(n^4\),超限的。
因为相邻两个数的差值不超过 3,所以优化一下,\(dp[i][a][b][c]\) 表示将第 \(i\) 个数放到容器后,第一个容器最后一个数与 \(i\) 的差值为 \(a\),第二个容器最后一个数与 \(i\) 的差值为 \(b\),第三个容器最后一个数与 \(i\) 的差值为 \(c\)。
如果数与 \(i - 1\) 的差值为 3,那么对于 \(i\),它的差值一定大于 3 了,所以大于 3 的都可以不用记录,因为对答案没有影响。
特殊定义 \(dp[i][4][4][4]\) 为容器为空的状态,所以 \(dp[0][4][4][4] = 1\)。
代码:
#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e4 + 10, mod = 1e9 + 7;
LL n, m, dp[N][5][5][5];
bool v[N][4];
LL to(LL x){
return (x == 4) ? 4 : min(x + 1, 3LL);
}
int main(){
cin >> n >> m;
for (int i = 0; i < m; i ++ ){
LL x, y;
cin >> x >> y;
v[x][y] = true;
}
dp[0][4][4][4] = 1;
for (int i = 0; i < n; i ++ ){
for (int a = 0; a <= 4; a ++ ){
for (int b = 0; b <= 4; b ++ ){
for (int c = 0; c <= 4; c ++ ){
if (a != 3 && !v[i + 1][1])
dp[i + 1][0][to(b)][to(c)] = (dp[i + 1][0][to(b)][to(c)] + dp[i][a][b][c]) % mod;
if (b != 3 && !v[i + 1][2])
dp[i + 1][to(a)][0][to(c)] = (dp[i + 1][to(a)][0][to(c)] + dp[i][a][b][c]) % mod;
if (c != 3 && !v[i + 1][3])
dp[i + 1][to(a)][to(b)][0] = (dp[i + 1][to(a)][to(b)][0] + dp[i][a][b][c]) % mod;
}
}
}
}
LL ans = 0;
for (int a = 0; a <= 3; a ++ )
for (int b = 0; b <= 3; b ++ )
for (int c = 0; c <= 3; c ++ )
ans = (ans + dp[n][a][b][c]) % mod;
cout << ans << "\n";
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号