比赛过程总结（个人记忆，有些细节也忘了）：
刚开始的时候，从头开始扫了一遍题目，感觉 A,C,E,F,J,L 可以做，先选择开了 L，看了一会儿，wcj 觉得有思路了，于是他和 wd 讲解（我没懂），然后我就放心去看了一下 A（这么简单？迟迟不敢确定，就又看了两遍），然后觉得就是水题，于是直接讲了一下题目和思路，让 wd 开始码，wcj 想 L 和 C，9分钟的时候才一发过了 A。
然后看了一下榜，发现 M 可以冲，于是 wd 去看了 M，wd 和 wcj 觉得 L 思路没问题了，于是 wcj 开始码 L，然后27分钟的时候交了一发，错了，于是我和 wcj 开始重新思考 L，wd 去看 M ，我去读了一下 L 题（刚开始没怎么读），出了一个测试把之前的思路否定掉了，我们重新确定了一下题目意思，然后他们俩开始想 L，wd 没看懂 M，只能确定是博弈，让我去看，在 55 分钟的时候他们把 L 给过了。
我给他们讲了一下 M，然后发现还是讲不通，于是他们开始思考 C，我继续 M，期间我写出来了一个思路，觉得没啥问题，然后问了 wd 的意见，觉得 OK，就交了一发 M，WA 了，于是 wd 开始和我一起想 M，wcj 单开 C。wd 讲了他的思路，觉得没错，然后我改了又交了一发，又错...然后我们自以为发现了问题，又改了一下，重新再交，还是 WA...这中间好几次发现了题目中很多细节读错了，心态有点微妙的起伏，然后 wd 决定把 M 给我，他们主攻 C，我暴力跑了一些数据，然后试了一下，觉得输出就是 0（后面脑子很乱，糊里糊涂地就这么觉得了，其实想错的），然后在快三小时的时候交了，过了。
帮忙搞 C，测试数据一直不对，发现题目的理解错了，改了之后，在三小时十分钟的时候一发过了。
于是开始看 F 和 J，J 一开始看是图的东西，于是交给 wd，wcj 和我去看 F，我给 wcj 翻译了一下 F，他觉得可以搞，于是他想了一个思路，但是我和 wd 听不懂，让他码了试试，我给他写了一些测试集，过了，然后交上去直接 WA 掉，然后我们决定双开，wcj 弄 F，我和 wd 弄 J。
然后 wd 喊我去搞 J，他觉得是最短路+完全背包，我看了一下，确实是这样，于是想了一下怎么搞，然后 wd 开始用链式前向星存图，跑dijkstra，他测了一下，没问题，然后我开始写完全背包，搞了一下，感觉时间复杂度不太行（我多写了一个循环，一直觉得优化不掉），抱着试一试的想法，觉得肯定是 TLE，交了一发，WA。我觉得背包没问题，让 wd 改 dijkstra，他改了两份，都 WA 了，然后改成 bfs，TLE。然后我想着优化背包，最后结束的时候交了几发，都错了，这期间 wcj 也尝试交了几发 F，都没过。
比赛结束...
结束后问了一下其他组背包咋搞的，发现我比赛的时候 nt 了，于是改了再交了几发（用 dijkstra 和 bfs 都试了一下），还是 WA。
吃完饭回来我想到我们 bfs 的一个问题，于是 wd 改了一下，交上去，AC了。
补题（做出来的也自己重新写了一下）：
题目链接：
https://codeforces.com/gym/103055
A. League of Legend
题目大意：
游戏比赛中红方和蓝方各有五人，每个人的有一个 HP，每一次操作使对方任意一位队员的血量减去1，若某支队全员 HP <= 0，另一只队伍获胜，蓝方先手，判断哪一方胜利。
思路：
水题，直接求和判断大小。
代码：
#include <bits/stdc++.h>
using namespace std;
#define LL long long
LL a, b, num;
void solve(){
for (int i = 1; i <= 5; i++){
cin >> num;
a += num;
}
for (int i = 1; i <= 5; i++){
cin >> num;
b += num;
}
cout << ((a >= b) ? "Blue\n" : "Red\n");
}
int main(){
solve();
return 0;
}
C. Cube
题目大意：
给 8 个点的三维坐标，判断他们是否能组成一个正六边形。
思路：
计算每个点到其它所有点的距离，然后将距离加入 map 中，小的两个距离数量应该是 12，即临边和某个面的对角线，大的一个应该是 4，即整个六边形的对角线。
ps：要考虑点重合的情况
代码：
通过 STL 解，所有距离存了两遍
#include <bits/stdc++.h>
using namespace std;
#define LL long long
LL T;
double myPow(double x){
return x * x;
}
void solve(){
map <double, int> mp;
int k = 0;
int num[4] = {0, 24, 24, 8};
vector <double> x(8), y(8), z(8);
for (int i = 0; i < 8; i++)
cin >> x[i] >> y[i] >> z[i];
for (int i = 0; i < 8; i++)
for (int j = 0; j < 8; j++){
if (i == j) continue;
double d = myPow(x[i] - x[j]) + myPow(y[i] - y[j]) + myPow(z[i] - z[j]);
mp[d] += 1;
}
for (auto &x : mp){
k++;
if (k == 4 || x.second != num[k]){
cout << "NO\n";
return;
}
}
cout << "YES\n";
}
int main(){
cin >> T;
while (T--)
solve();
return 0;
}
数组直接算，所有距离只存了一遍
#include <bits/stdc++.h>
using namespace std;
#define LL long long
LL T;
double myPow(double x){
return x * x;
}
void solve(){
map <double, int> mp;
int cnt = 0, d[100];
vector <double> x(8), y(8), z(8);
for (int i = 0; i < 8; i++)
cin >> x[i] >> y[i] >> z[i];
for (int i = 0; i < 8; i++)
for (int j = i + 1; j < 8; j++)
d[++cnt] = myPow(x[i] - x[j]) + myPow(y[i] - y[j]) + myPow(z[i] - z[j]);
sort(d + 1, d + cnt + 1);
if (d[1] != 0 && d[13] != 0 && d[25] != 0 && d[1] == d[12] && d[13] == d[24] && d[25] == d[28] && d[1] * 2 == d[13] && d[1] * 3 == d[28]) cout << "YES\n";
else cout << "NO\n";
}
int main(){
cin >> T;
while (T--)
solve();
return 0;
}
F. Fair Distribution
题目大意：
\(有 n 个机器人和 m 个能量棒\)，在一步操作中只能减少机器人的数量或者增加能量棒的数量，求最少操作几步才能实现能量棒的数量变成机器人的数量的倍数。
思路：
当 \(n >= m\) 时，直接输出 \(n - m\) 即可。
当 \(n < m\) 时，\(n\) 的变化影响直接影响了 \(m\)，可以循环，设最后剩下的机器人的数量是 \(l\)，则需要的能量棒的数量是 \(\lceil m / l \rceil * l\)，那么操作的步数是 \(n - l + \lceil m / l \rceil * l - m\)，因为 \(\lceil m / l \rceil * l = \lfloor (m - 1) / l \rfloor * l + l\)，所以最后的操作步数是 \(n - m + \lfloor (m - 1) / l * l \rfloor\)。
但是直接从 1 到 \(n\) 跑一遍会超时，在计算步数的公式中可以发现，连续的一些数的 \(\lfloor (m - 1) / l \rfloor\) 的值是相同的，那最后的步数就与 \(l\) 成正相关，所以对于 \(\lfloor (m - 1) / l \rfloor\) 值相同的区间，只需要计算最小的 \(l\) 的步数即可。
于是考虑分块的思想，没必要全部遍历，而是遍历不同的 \(\lfloor (m - 1) / l \rfloor\) 计算最小值就是答案。
代码：
#include <bits/stdc++.h>
using namespace std;
int T, n, m;
void solve(){
cin >> n >> m;
if (n >= m) cout << n - m << "\n";
else {
int ans = 1e9;
for (int l = 1; l <= n;){
int r = min(n, (m - 1) / ((m - 1) / l));
ans = min(ans, n - m + (m - 1) / l * l);
l = r + 1;
}
cout << ans << "\n";
}
}
int main(){
cin >> T;
while(T--)
solve();
return 0;
}
G. Wall Game
题目大意：
在有很多蜂巢的地图上，x 轴在水平轴上，y 轴是 x 轴逆时针旋转 60 度角而成，每个蜂巢相邻六个蜂巢。
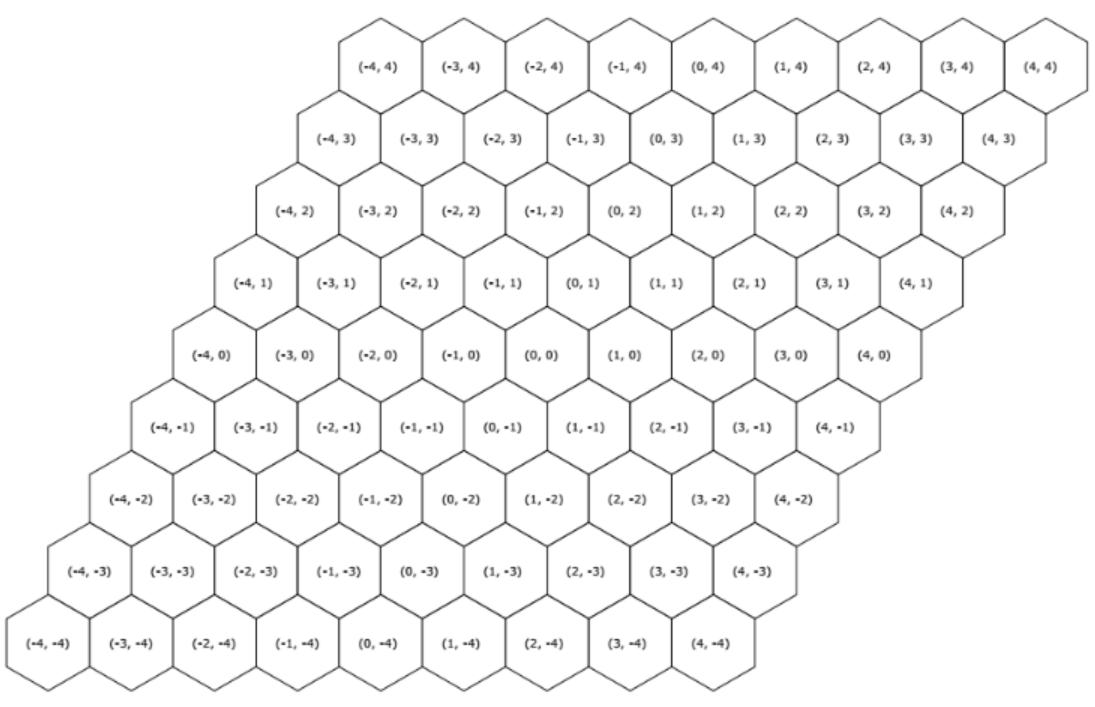
现有两种操作，操作一是攻占一个蜂巢，攻占蜂巢后会在攻占的蜂巢和未攻占的蜂巢之间建立围墙，操作二是查询从该蜂巢出发，不穿过任何围墙能接触到几座围墙。
思路：
为了实现多个攻占的蜂巢合为一体，可以想到并查集，而点的坐标是二维的，可以通过 \(map\) 让二维的坐标转化为一个值，方便并查集操作。
当新攻占了一个蜂巢之后，需要和周围已攻占的蜂巢进行一个合并操作。一个蜂巢的围墙是 6 座，与相邻的蜂巢合并后，相邻的那条边的围墙拆除，减去 2.
代码：
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
#define fi first
#define mp make_pair
#define pii pair <int, int>
#define se second
int n, op, x, y, cnt, fa[N], ans[N];
int dx[] = {0,1,1,0,-1,-1}, dy[] = {1,0,-1,-1,0,1};
map <pii, int> idx;
int find(int x){
if (fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
void add(int x, int y){
pii t = mp(x, y);
idx[t] = ++cnt;
ans[idx[t]] = 6;
for (int i = 0; i < 6; i++){
int nx = t.fi + dx[i], ny = t.se + dy[i];
pii now = mp(nx, ny);
if (idx[now]){
int a = find(idx[t]), b = find(idx[now]);
if (a != b){
fa[b] = a;
ans[a] = ans[a] + ans[b] - 2;
}
else ans[a] -= 2;
}
}
}
void solve(){
scanf("%d%d%d", &op, &x, &y);
if (op == 1) add(x, y);
else {
pii t = mp(x, y);
cout << ans[find(idx[t])] << "\n";
}
}
void init(){
for (int i = 1; i <= n; i++) fa[i] = i;
}
int main(){
cin >> n;
init();
while (n--)
solve();
return 0;
}
J. Grammy and Jewelry
题目大意：
\(一个 n 个顶点， m 条边的无向图\)，除了起点外每个顶点上有无限个宝藏，Grammy 从 1 出发，去其它点拿宝藏，走每一条边都要花 1 单位时间，Grammy 拿到宝藏并将宝藏放回起点才能获得该宝藏的价值，每次最多拿一个宝藏，问在 \(t\) 单位时间内能拿到宝藏的最大价值是多少。
思路：
首先计算起点到其它点的最短时间是多少，即求最短的路径，每条边的长度就是 1，可以通过 bfs、dijkstra 等等去实现，然后就是一个多重背包问题，每个物品的价值已知，体积是路径长度的两倍（因为拿到后还要返回起点，且一次只能拿一个宝藏），而背包的总容量就是限定的时间。
代码：
链式前向星 + bfs
#include <bits/stdc++.h>
using namespace std;
const int N = 3e3 + 10;
int n, m, t, f[N], v[N], w[N], ver[2 * N], edge[2 * N], Next[2 * N], head[2 * N], d[N], tot;
void bfs(){
queue <int> q;
q.push(1); d[1] = 1;
while (q.size()){
int x = q.front(); q.pop();
for (int i = head[x]; i; i = Next[i]){
int y = ver[i];
if (d[y]) continue;
d[y] = d[x] + 1;
w[y] = w[x] + 1;
q.push(y);
}
}
}
void add(int x, int y, int z){
ver[++tot] = y;
edge[tot] = z;
Next[tot] = head[x];
head[x] = tot;
}
void solve(){
cin >> n >> m >> t;
for (int i = 2; i <= n; i++)
cin >> v[i];
for (int i = 1; i <= m; i++){
int x, y;
cin >> x >> y;
add(x, y, 1);
add(y, x, 1);
}
bfs();
for (int i = 1; i <= n; i++)
w[i] *= 2;
for (int i = 2; i <= n; i++)
for (int j = w[i]; j <= t; j++)
f[j] = max(f[j], f[j - w[i]] + v[i]);
for (int i = 1; i <= t; i++)
cout << f[i] << " \n"[i == t];
}
int main(){
solve();
return 0;
}
vector + bfs
#include <bits/stdc++.h>
using namespace std;
const int N = 3e3 + 10;
int n, m, t, f[N], v[N], w[N], d[N];
vector <int> e[N];
void bfs(){
queue <int> q;
q.push(1); d[1] = 1;
while (q.size()){
int x = q.front(); q.pop();
for (auto &y : e[x]){
if (d[y]) continue;
d[y] = d[x] + 1;
w[y] = w[x] + 2;
q.push(y);
}
}
}
void solve(){
cin >> n >> m >> t;
for (int i = 2; i <= n; i++)
cin >> v[i];
for (int i = 1; i <= m; i++){
int x, y;
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
bfs();
for (int i = 2; i <= n; i++)
for (int j = w[i]; j <= t; j++)
f[j] = max(f[j], f[j - w[i]] + v[i]);
for (int i = 1; i <= t; i++)
cout << f[i] << " \n"[i == t];
}
int main(){
solve();
return 0;
}
L. String Freshman
题目大意：
给出了一个计算字符串 \(S 中有多少个子串等于 T\) 的代码
int Find_Answer(){
int j = 1, ans = 0;
for (int i = 1; i <= n; i++){
if (S[i] != T[j]) j = 1;
if (S[i] == T[j]) j++;
if (j > m){
ans++;
j = 1;
}
}
return ans;
}
已知字符串 \(T 以及 T 的长度 m\)，判断对于所有 \(S\) 该算法计算得正不正确，若错误，输出"Wrong Answer"，若正确，输出"Correct"。
思路：
该算法使用了\(kmp\)的思路，但是 \(S\) 中的指针没有前移，这就导致若 \(T\) 的第二位开始出现了一个字符与第一个字符相同时，该算法就会计算错误。
代码：
#include <bits/stdc++.h>
using namespace std;
int m;
string t;
void solve(){
cin >> m >> t;
for (int i = 1; i < m; i++)
if (t[i] == t[0]){
cout << "Wrong Answer\n";
return;
}
cout << "Correct\n";
}
int main(){
solve();
return 0;
}
M. Game Theory
题目大意：
\(n 个人，1 个老师，n - 1\) 个学生，老师和学生玩一个游戏，老师随机且独立地出一个数 \(x\)，一个学生出一个数 \(y(1 <= x,y <= 20)\)，给出数时，自己失去相应的分数，同时对方获得这个分数，若 \(x 严格大于 y\)，则老师获胜，该学生要多给老师 10 分，反之，则相反，每个学生都不知道老师出的是什么数，但是学生足够聪明，都选择最优策略去获取最大的分数，求老师最终会获得多少分。
思路：
学生足够聪明，于是学生会选择比老师大 1 的数去获得最高的分数，但是学生又不知道老师出的是什么数，同时老师出的数是随机的，由于总体的得分期望是 0，所以结果为 0。
代码：
#include <bits/stdc++.h>
using namespace std;
int main(){
cout << "0.0000\n";
return 0;
}
