浅谈线段树(by Shine_hale)
一. 线段树是什么?
线段树,顾名思义,就是将区间变成线段进行处理
如图可以看出,将1-10这个线段不断拆分,进而得到子节点;
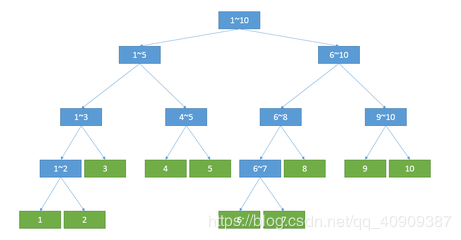
摘自互联网
二、为什么要用线段树
线段树修改简单,方便快捷,同时;在查询上可以使时间复杂度到达O(1),这很厉害了
同时不同于RMQ问题,可以在线进行修改,不用花时间进行重构。
但是线段树有个缺点有个较大的常数。
话不多说,正式开始介绍,hale理解下的线段树大法
线段树,毕竟是树形结构,第一步当然是建树了
首先要有准备工作,处理左儿子,右儿子的问题
int ls(int p) {return p<<1;}//左儿子 int rs(int p) {return p<<1|1;}//右儿子
建树过程(递归建树)其实还有一种建树方法
zkw线段树 (但是我不会告诉你我不会的)嘤嘤嘤
void build(int p,int l,int r) { int mid=(l+r)>>1; if (l==r) { st[p].ans=a[l];return;} build(ls(p),l,mid); build(rs(p),mid+1,r); push_up(p); }
其实push_up本身就是向上回溯的过程
我只是把这个过程单独列了出来
void push_up(int p) { st[p].ans=st[ls(p)].ans+st[rs(p)].ans;}
接着介绍如何区间修改
为什么不介绍单点修改,其实很简单了,单点不就可以看成一个只包含自己的区间吗
那么对于区间操作,我们考虑引入一个名叫“lazylazy tagtag”(懒标记)的东西——之所以称其“lazylazy”,是因为原本区间修改需要通过先改变叶子节点的值,然后不断地向上递归修改祖先节点直至到达根节点,时间复杂度最高可以到达O(nlogn)O(nlogn)的级别。但当我们引入了懒标记之后,区间更新的期望复杂度就降到了O(logn)O(logn)的级别且甚至会更低.
void push_down(int p,int l,int r) { int mid=(l+r)>>1; st[ls(p)].add+=st[p].add; st[rs(p)].add+=st[p].add; st[ls(p)].ans+=st[p].add*(mid-l+1); st[rs(p)].ans+=st[p].add*(r-mid); st[p].add=0; }
首先,懒标记的作用是记录每次、每个节点要更新的值,也就是delta,但线段树的优点不在于全记录(全记录依然很慢qwq),而在于传递式记录;
整个区间都被操作,记录在公共祖先节点上;只修改了一部分,那么就记录在这部分的公共祖先上;如果四环以内只修改了自己的话,那就只改变自己。
如果我们采用上述的优化方式的话,我们就需要在每次区间的查询修改时pushdown一次,以免重复或者冲突或者爆炸qwqqwq
那么对于pushdown而言,其实就是纯粹的pushup的逆向思维(但不是逆向操作): 因为修改信息存在父节点上,所以要由父节点向下传导lazy tag
那么问题来了:怎么传导pushdown呢?这里很有意思,开始回溯时执行pushup,因为是向上传导信息;那我们如果要让它向下更新,就调整顺序,在向下递归的时候pushdown就好了
void update(int nl,int nr,int l,int r,int p,int k) { if (nl<=l&&nr>=r) { st[p].ans+=k*(r-l+1); st[p].add+=k;return;} int mid=(l+r)>>1; push_down(p,l,r); if (nl<=mid) update(nl,nr,l,mid,ls(p),k); if (nr>mid) update(nl,nr,mid+1,r,rs(p),k); push_up(p); }
好了,区间修改了之后就该区间求和了
思想跟上面的差不多,大家自行理解就好了、
int query(int qx,int qy,int l,int r,int p) { int res=0; if (qx<=l&&qy>=r) return st[p].ans; push_down(p,l,r); int mid=(l+r)>>1; if (qx<=mid) res+=query(qx,qy,l,mid,ls(p)); if (qy>mid) res+=query(qx,qy,mid+1,r,rs(p)); return res; }
最后插一句
区间乘法的维护需要注意先后顺序同时要注意取模,一定要一步一取模啊
void push_down(int p,int l,int r) { int mid=(l+r)>>1; st[ls(p)].nul=(st[ls(p)].nul*st[p].nul)%Mod; st[rs(p)].nul=(st[rs(p)].nul*st[p].nul)%Mod; st[ls(p)].add=(st[ls(p)].add*st[p].nul+st[p].add)%Mod; st[rs(p)].add=(st[rs(p)].add*st[p].nul+st[p].add)%Mod; st[ls(p)].ans=(st[ls(p)].ans*st[p].nul+st[p].add*(mid-l+1))%Mod; st[rs(p)].ans=(st[rs(p)].ans*st[p].nul+st[p].add*(r-mid))%Mod; st[p].nul=1; st[p].add=0; }
最后的最后,我知道大家不想听我扯这么多
所以直接暴力上代码吧,嘤嘤嘤
#include<bits/stdc++.h> using namespace std; const int M=200010; int m,n,k,p,a[M]; struct node { int ans; int add; }; node st[M<<2]; int ls(int p) {return p<<1;} int rs(int p) {return p<<1|1;} void push_up(int p) { st[p].ans=st[ls(p)].ans+st[rs(p)].ans;} void build(int p,int l,int r) { int mid=(l+r)>>1; if (l==r) { st[p].ans=a[l];return;} build(ls(p),l,mid); build(rs(p),mid+1,r); push_up(p); } void push_down(int p,int l,int r) { int mid=(l+r)>>1; st[ls(p)].add+=st[p].add; st[rs(p)].add+=st[p].add; st[ls(p)].ans+=st[p].add*(mid-l+1); st[rs(p)].ans+=st[p].add*(r-mid); st[p].add=0; } void update(int nl,int nr,int l,int r,int p,int k) { if (nl<=l&&nr>=r) { st[p].ans+=k*(r-l+1); st[p].add+=k;return;} int mid=(l+r)>>1; push_down(p,l,r); if (nl<=mid) update(nl,nr,l,mid,ls(p),k); if (nr>mid) update(nl,nr,mid+1,r,rs(p),k); push_up(p); } int query(int qx,int qy,int l,int r,int p) { int res=0; if (qx<=l&&qy>=r) return st[p].ans; push_down(p,l,r); int mid=(l+r)>>1; if (qx<=mid) res+=query(qx,qy,l,mid,ls(p)); if (qy>mid) res+=query(qx,qy,mid+1,r,rs(p)); return res; } int main() { int x,y,z; scanf("%d",&n); for (int i=1;i<=n;i++) scanf("%d",&a[i]); build(1,1,n); scanf("%d",&m); for (int i=1;i<=m;i++) { scanf("%d",&k); switch(k) { case 1:{scanf("%d%d%d",&x,&y,&z); update(x,y,1,n,1,z); break;} case 2:{scanf("%d%d",&x,&y); printf("%d\n",query(x,y,1,n,1)); break;} } } return 0; }
hale还没学会别的高级操作,所以先就此搁笔了,愿大家越来越强

