非递归方式实现二叉树的后序遍历

Description
给定一个二叉树，用非递归的方式实现二叉树的后序遍历。
Input
输入第一行为一个整数 n（1 <= n <= 100000），表示二叉树的节点个数。
接下来共有 n 行，每行有两个整数 l 和 r，分别表示第 i （i为每一行的行号）个节点的左孩子和右孩子下标，值为 0 表示当前节点没有左孩子/右孩子。根节点的下标始终为 1。
Output
输出二叉树后续遍历的结果, 用空格分隔。
Sample Input

5
2 4
5 3
0 0
0 0
0 0

Sample Output

5 3 2 4 1

Hint

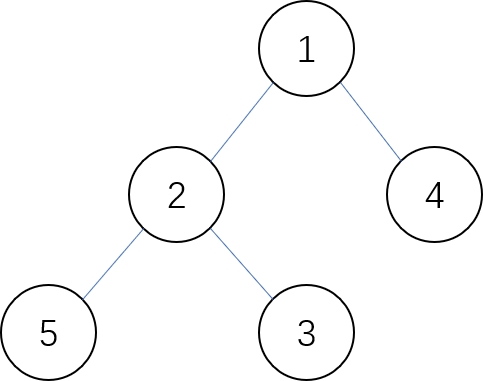
以第一组测试用例为例，二叉树共 5 个节点，接下来 5 行输入。

第 1 行为 2 4，表示节点编号为 1 的节点（根节点）的左孩子为编号为 2 的节点，右孩子为编号为 4 的节点。

第 2 行为 5 3，表示节点编号为 2 的节点的左孩子为编号为 5 的节点，右孩子为编号为 3 的节点。

后续输入均为 0，表示剩下编号为 3、4、5 的节点均无左/右孩子节点。

 

Answer

因为题目的输入是按编号顺序输入各个节点的数据，每个节点指出左右孩子。所以二叉树的建立可以采用顺序存储结构，通过节点类型的一维动态数组构建二叉树。因为第一行已经输入了节点数，数组容量已知，直接new一个出来就行。

#include <iostream>
#include <vector>
#include <stack>
#include <algorithm>

using namespace std;

typedef struct BiTNode {
    int data;
    BiTNode *leftChild;
    BiTNode *rightChild;
} BiTNode, *BiTree;

vector<int> postorderTraversal(BiTree root) {
    vector<int> result;
    stack<BiTree> st;
    if (root == nullptr)return result;
    st.push(root);
    while (!st.empty()) {
        BiTree p = st.top();
        st.pop();
        result.push_back(p->data);
        if (p->leftChild != nullptr)st.push(p->leftChild);
        if (p->rightChild != nullptr)st.push(p->rightChild);
    }
    reverse(result.begin(), result.end());
//比较偷懒的办法，按照迭代前序遍历的程序，从中-左-右改成中-右-左，然后颠倒个个儿变成左-右-中。
    return result;
}

void Display(const vector<int> &res, int n) {
    for (int i = 0; i < n; i++) {
        cout << res[i] << ' ';
    }
}

BiTree CreateTree(int n) {
    int l, r;
    BiTNode *T = new BiTNode[n];
    for (int i = 0; i < n; i++) {
        T[i].data = i + 1;
        cin >> l;
        cin >> r;
        if (l == 0)T[i].leftChild = nullptr;
        else T[i].leftChild = &T[l - 1];
        if (r == 0)T[i].rightChild = nullptr;
        else T[i].rightChild = &T[r - 1];
    }
    return T;
}

int main() {
    int n;
    cin >> n;
    BiTree T = CreateTree(n);
    vector<int> res = postorderTraversal(T);
    Display(res, n);
}

 Tip：

作为新手，写代码不熟练，一开始没有 BiTNode *T = new BiTNode[n]; 而是直接 BiTNode T[n];  只是定义而并没有为数组分配空间，后面的取地址自然错了，都没有空间，何来的地址？ 

同样，使用vector时，如果给了大小，就一开始直接 vector<BiNode> T(n); 就相当于new了一个n大小的容器出来，这样才分配了地址空间，否则不加（n）等于vector容量为0。