BZOJ 1035: [ZJOI2008]Risk 题解

这题做的神尴尬😅

 开始的时候很无脑的就用简单的卷包裹瞎搞，想到找当前联通块的某一个边就好了，然后各种bug搞法果断WA。

突然发现有坑，样例二没好好看。。。MDZZ又调了半天，突然发现不止一个坑。。。哭晕。。。

于是前前后后花了一天时间调一个错误的算法。MDZZMDZZMDZZ

（下次一定要想清楚了再敲）

但仔细想想，MD这不是计算几何的码农题么？那本超厚的计算几何黄书上不给出了找坑的方法么？不就是扫描线瞎搞么？

（害怕写代码的蒟蒻开始不自觉的自发颤抖了(´･_･`)）

但是还有更快捷一点的搞法。参考了一篇参考了Claris的题解的题解，嗯，只要添加几条线段手动填坑就可以了。

（可惜蒟蒻不会写扫描线只好 \( O(m^2) \) 暴力了(￣▽￣)）

前后花了一天半的时间（算上第二天早上去看《侏罗纪世界2》的时间和第三天早上睡懒觉到十点的话）对着数据用几何画板调在学校OJ上提交十次终于AC了好激动好激动^o^

而且理论 \( O(m^2) \) 的复杂度实际上跑得很快（404ms）

实际上复杂度应该是 \( O(m\ \times 环的个数 + m\ n) \)，而环的话看数据中给的甚至不会到 \( O(log\ m) \)。

大体思路是先dfs每个边联通块，找到最左边的点 \( t \)，然后作一条向左的射线，找到最近的相交线段 \( s \)，连接 \( t \) 和 \( s \) 的任意一个端点，这样就填上坑了。

坑填好后对每个点用一样的方法找到水平距离最近的线段（左右都可以），然后就可以随便卷包裹了（因为没有坑，所以毫无顾虑放心跑）。

不过我好像哪里写挂了，像这样：

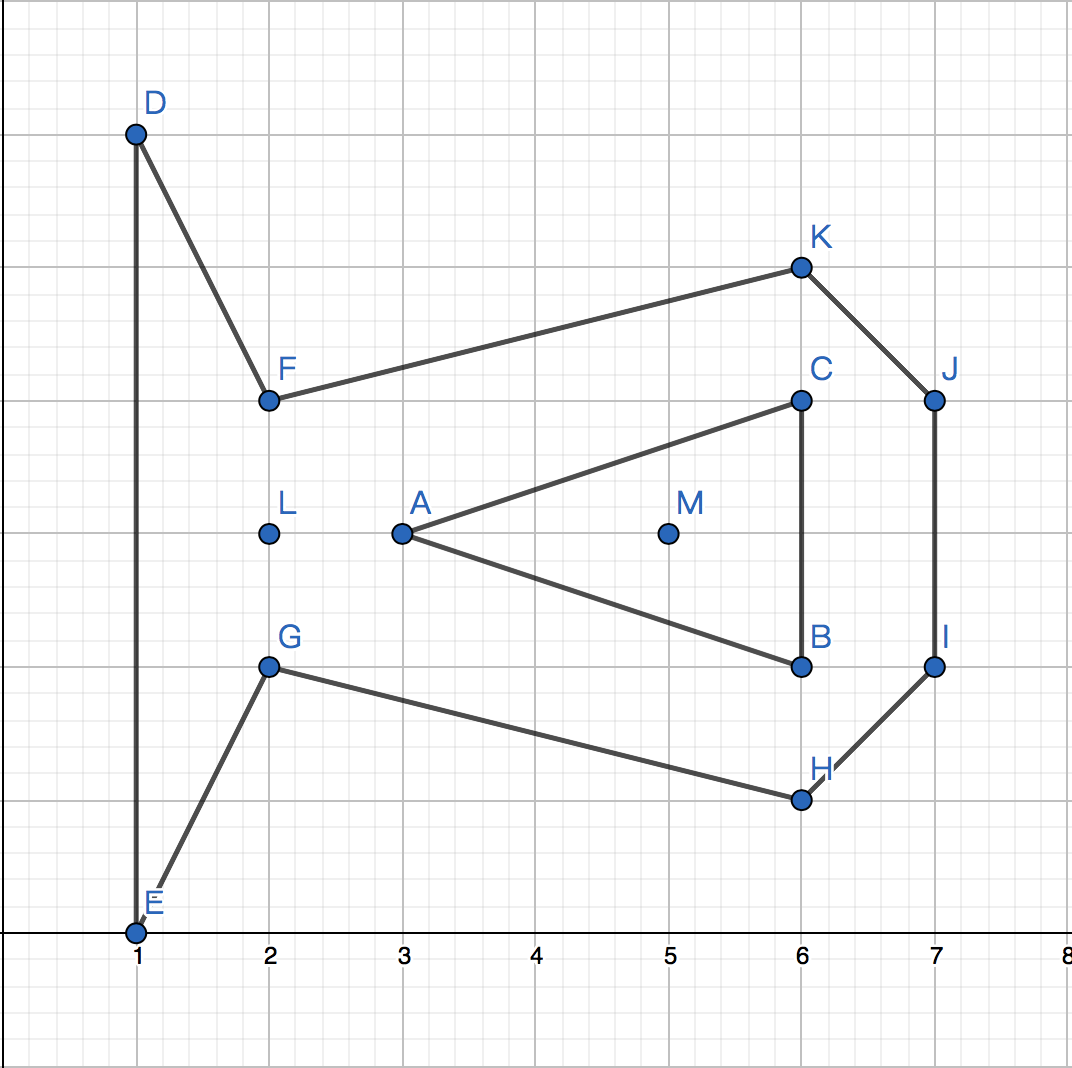
假如 \( A \) 是一个最左侧的点，然后要连接 \( A - BC \)，会跨过其它的线段，看起来不像是理想中的面剖分。

我的程序跑出来是 \( 0\ 0 \)。我果然是个大蒟蒻啊！

目测是因为我没有用扫描线的原因，如果用扫描线的话。。。

等等，突然发现原话是“向交点连边”。恍然大悟。。。

要把原来的边拆成两条新的线段啊。怎么没想到呢。话说题目数据好水啊^_^

不过这样又有新麻烦了。如果连的边经过某个队伍怎么办？既然连的边只经过一个联通块，而且就是那支队伍所在的联通块，目测瞎搞是可以的(￣▽￣)

不过又有麻烦了。如果两条边共线怎么办？必须要拆。但是我实在是懒得改了。

可能还有我没想到的细节。如果用扫描线的话，感觉方便多了。。。

必须要学扫描线了(T ^ T)