Fibonacci
Interesting Fibonacci
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 672 Accepted Submission(s): 116
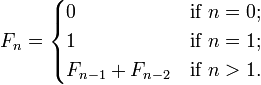That is, after two starting values, each number is the sum of the two preceding numbers. The first Fibonacci numbers (sequence A000045 in OEIS), also denoted as F[n]; F[n] can be calculate exactly by the following two expressions: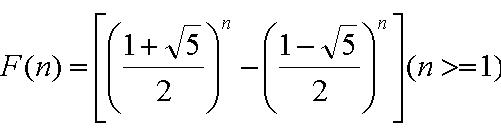 
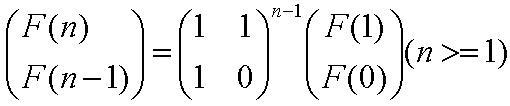A Fibonacci spiral created by drawing arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13, 21, and 34;So you can see how interesting the Fibonacci number is. Now AekdyCoin denote a function G(n)
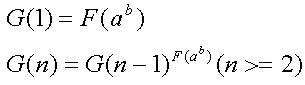Now your task is quite easy, just help AekdyCoin to calculate the value of G (n) mod CIn mathematics, Fibonacci numbers or Fibonacci series or Fibonacci sequence are the numbers of the following integer sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...
By definition, the first two numbers in the Fibonacci sequence are 1 and 1, and each subsequent number is the sum of the previous two. In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation Fn = Fn - 1 + Fn - 2 with seed values F1 = 1 and F2 = 1.
And your task is to find ΣFiK, the sum of the K-th power of the first N terms in the Fibonacci sequence. Because the answer can be very large, you should output the remainder of the answer divided by 1000000009.
Input
There are multiple test cases. The first line of input is an integer T indicates the number of test cases. For each test case:
There are two integers N and K (0 <= N <= 1018, 1 <= K <= 100000).
Output
For each test case, output the remainder of the answer divided by 1000000009.
Sample Input
5 10 1 4 20 20 2 9999 99 987654321987654321 98765
Sample Output
143 487832952 74049690 113297124 108672406
Hint
The first test case, 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 = 143.
The second test case, 120 + 120 + 220 + 320 =3487832979, and 3487832979 = 3 * 1000000009 + 487832952, so the output is 487832952.
Author: ZHOU, Yuchen
2014年蓝桥杯的第九题是这样描述的：
给定Fibonacci数列F[]，其中，
，求表达式
的值。其中
E - 喵喵的遗憾
Problem Description
喵喵因为太弱，没有进Final，终身遗憾。她就挂在了这个题目上。
已知：
F0 = 1 , F1 = 1 , F2 = 2 , Fn = Fn-1+Fn-2
求：
FFFn Mod P
( 也就是 F[ F[ F[n] ] ] % P )
Input
第一行一个整数 T 代表数据组数(T ≤ 20000)。 <del> 
喵以人格担保时限肯定够！！！</del>
以下每行两个整数 N , P (0 ≤ N ≤ 109 , 1 ≤ P ≤ 109)
Output
Sample Input
4 1 2 2 3 4 35 4 31
Sample Output
1 2 34 3
Hint
F1 = 1 , F1 = 1 , F1 = 1
F2 = 2 , F2 = 2 , F2 = 2
F4 = 5 , F5 = 8 , F8 = 34
1 #include <cstdio> 2 #include <cstring> 3 #include <queue> 4 #include <map> 5 #include <cmath> 6 #include <iostream> 7 #include <time.h> 8 #include <algorithm> 9 using namespace std; 10 #define FF(i,N) for(int i=0;i<2;i++) 11 #define ll long long 12 #define maxn (1<<20) 13 struct mat{ ll m[2][2]; }; 14 ll n, s, k, t, p ,x , y, cnt, num, ans; 15 ll gcd(ll a, ll b){ return b ? gcd(b, a%b) : a; } 16 ll a[1005],b[105],c[105],pri[maxn],prv[maxn],GG[maxn]; 17 mat A; 18 mat Mul(mat a, mat b, ll mod){ 19 mat res; 20 FF(i, 2)FF(j, 2)res.m[i][j] = 0; 21 FF(i, 2)FF(j, 2)FF(k,2) 22 res.m[i][j] = (res.m[i][j]+a.m[i][k] * b.m[k][j]) % mod; 23 return res; 24 } 25 mat Pow(mat a, ll b, ll mod){ 26 mat res; 27 FF(i,2)FF(j,2)res.m[i][j] = (i == j); 28 while (b){ 29 if (b & 1)res = Mul(res, a, mod); 30 a = Mul(a, a ,mod); 31 b >>= 1; 32 } 33 return res; 34 } 35 ll POW(ll a, ll b, ll mod){ 36 a = a%mod; 37 ll res = 1; 38 while (b){ 39 if (b & 1)res = res*a%mod; 40 a = a*a%mod; 41 b >>= 1; 42 } 43 return res; 44 } 45 ll Loop(ll p, ll mod){ 46 mat res = Pow(A, p - 1, mod); 47 if ((res.m[0][0] + res.m[1][0])%mod == 1 && (res.m[0][1] + res.m[1][1])%mod == 0)return 1; 48 return 0; 49 } 50 ll G(ll p){ 51 if (p < 1000000 && GG[p] != -1)return GG[p]; 52 ll mod = p; k = 0; 53 if (POW(5, (p - 1)>>1, mod) == 1)p = p - 1; 54 else p = 2 * (p + 1); 55 int stop = sqrt(1.0*p); 56 for (int i = 1; i <= stop; i++){ 57 if (p%i)continue; 58 a[k++] = i; 59 if(i*i!=p)a[k++] = p / i; 60 } 61 sort(a, a + k); 62 for (int i = 0; i < k;i++) 63 if (Loop(a[i], mod)){ 64 if (mod < 1000000)return GG[mod] = a[i]; 65 return a[i]; 66 } 67 } 68 void init(){ 69 A.m[0][0] = 1; A.m[0][1] = 1; 70 A.m[1][0] = 1; A.m[1][1] = 0; 71 } 72 ll LOOP(ll p){ 73 s = 1; num = 0; c[0] = 0; 74 for (int i = 0; pri[i]*pri[i] <= p; i++){ 75 c[num] = 0; 76 if (p%pri[i] == 0){ 77 b[num] = pri[i]; 78 while (p%pri[i] == 0)p /= pri[i], c[num]++; 79 num++; 80 } 81 } 82 if (p>1)c[num] = 1, b[num++] = p; 83 for (int i = 0; i < num; i++){ 84 if (c[i]){ 85 if (b[i] == 2)y = 3; 86 else if (b[i] == 3)y = 8; 87 else if (b[i] == 5)y = 20; 88 else y = G(b[i]); 89 for (int j = 1; j < c[i]; j++)y = y*b[i]; 90 s = s/gcd(s, y)*y; 91 } 92 } 93 return s; 94 } 95 int main(){ 96 memset(GG, -1, sizeof GG); 97 int stop = sqrt(1.0 * 1000000); 98 for (int i = 2; i<=stop;i++) 99 if (!prv[i]) 100 for (int j = i*i; j <= 1000000;j+=i) 101 if (!prv[j])prv[j] = 1; 102 for (int i = 2; i <= 1000000; i++)if (!prv[i])pri[cnt++] = i; 103 int T;scanf("%d",&T); 104 while (T--){ 105 init(); 106 scanf("%d%d", &n, &p); 107 if (p == 1){ printf("0\n"); continue; } 108 if (n == 0){ printf("1\n"); continue; } 109 ll mod = p; 110 ll mod1 = LOOP(p); 111 ll mod2 = LOOP(mod1); 112 mat res; 113 res = Pow(A, n-1, mod2); 114 n = (res.m[0][0] + res.m[1][0]) % mod2; 115 res = Pow(A, (n + mod2 - 1) % mod2, mod1); 116 n = (res.m[0][0] + res.m[1][0]) % mod1; 117 res = Pow(A, (n + mod1 - 1) % mod1, mod); 118 ans = (res.m[0][0] + res.m[1][0]) % mod; 119 printf("%d\n", ans); 120 } 121 return 0; 122 }
这道题卡的地方，硬是找了半天都没找到，最后发现，n=0时，有些p输不出答案，估计是n-1小于0了那些地方就卡住了。。。Pow(A,n-1,mod)这里0 0。。。一开始写的是把最外面的那层再求一个循环节，
其实没必要，第一个n又不会超ll ，而且快速幂至少比求循环节快点，然后那时写的代码又戳，这个地方那时候不是这么写，多求了个循环节，n=n%s;Pow(A,(n-1+s)%s,mod)所以那时就没这个问题，后面优化着就
出问题了。。。结果就卡了大半天。。。
3286: Fibonacci矩阵
Time Limit: 15 Sec Memory Limit: 128 MB Submit: 131 Solved: 29 [Submit][Status]Description
Input
八个用空格隔开的整数n, m, a, b, c, d, e, f，其中n, m, a, b, d, e为正整数，c, f为非负整数。
Output
一个整数，表示Fib[n][m]对2012182013取模的值。
Sample Input
Sample Output
HINT
n,m,a,b,c,d,e,f<=10^1000000
Source
优美的Fibonacci数列与矩阵
题目：http://codeforces.com/contest/392/problem/C
题意：给定Fibonacci数列F[]，令，求
的值。
广义Fibonacci数列找循环节
今天将来学习如何求广义Fibonacci数列的循环节。
问题：给定，满足
，求
的循
环节长度。
来源：http://acdreamoj.sinaapp.com/ 1075题
2 4 5
6 20
1 #include <cstdio> 2 #include <cstring> 3 #include <queue> 4 #include <map> 5 #include <cmath> 6 #include <iostream> 7 #include <time.h> 8 #include <algorithm> 9 using namespace std; 10 #define FF(i,N) for(int i=0;i<2;i++) 11 #define ll long long 12 #define maxn (1<<20) 13 struct mat{ ll m[2][2]; }; 14 ll n, s, k, t, p, x, y, cnt, num, ans; 15 ll gcd(ll a, ll b){ return b ? gcd(b, a%b) : a; } 16 ll a[1005], b[105], c[105], pri[maxn], prv[maxn], GG[maxn]; 17 mat A; 18 mat Mul(mat a, mat b, ll mod){ 19 mat res; 20 FF(i, 2)FF(j, 2)res.m[i][j] = 0; 21 FF(i, 2)FF(j, 2)FF(k, 2) 22 res.m[i][j] = (res.m[i][j] + a.m[i][k] * b.m[k][j]) % mod; 23 return res; 24 } 25 mat Pow(mat a, ll b, ll mod){ 26 mat res; 27 FF(i, 2)FF(j, 2)res.m[i][j] = (i == j); 28 while (b){ 29 if (b & 1)res = Mul(res, a, mod); 30 a = Mul(a, a, mod); 31 b >>= 1; 32 } 33 return res; 34 } 35 ll POW(ll a, ll b, ll mod){ 36 a = a%mod; 37 ll res = 1; 38 while (b){ 39 if (b & 1)res = res*a%mod; 40 a = a*a%mod; 41 b >>= 1; 42 } 43 return res; 44 } 45 ll Loop(ll p, ll mod){ 46 mat res = Pow(A, p - 1, mod); 47 if ((res.m[0][0] + res.m[1][0]) % mod == 1 && (res.m[0][1] + res.m[1][1]) % mod == 0)return 1; 48 return 0; 49 } 50 ll G(ll p){ 51 if (p < 1000000 && GG[p] != -1)return GG[p]; 52 ll mod = p; k = 0; 53 if (POW(5, (p - 1) >> 1, mod) == 1)p = p - 1; 54 else p = 2 * (p + 1); 55 int stop = sqrt(1.0*p); 56 for (int i = 1; i <= stop; i++){ 57 if (p%i)continue; 58 a[k++] = i; 59 if (i*i != p)a[k++] = p / i; 60 } 61 sort(a, a + k); 62 for (int i = 0; i < k; i++) 63 if (Loop(a[i], mod)){ 64 if (mod < 1000000)return GG[mod] = a[i]; 65 return a[i]; 66 } 67 } 68 void init(){ 69 A.m[0][0] = 1; A.m[0][1] = 1; 70 A.m[1][0] = 1; A.m[1][1] = 0; 71 } 72 ll LOOP(ll p){ 73 s = 1; num = 0; c[0] = 0; 74 for (int i = 0; pri[i] * pri[i] <= p; i++){ 75 c[num] = 0; 76 if (p%pri[i] == 0){ 77 b[num] = pri[i]; 78 while (p%pri[i] == 0)p /= pri[i], c[num]++; 79 num++; 80 } 81 } 82 if (p>1)c[num] = 1, b[num++] = p; 83 for (int i = 0; i < num; i++){ 84 if (c[i]){ 85 if (b[i] == 2)y = 3; 86 else if (b[i] == 3)y = 8; 87 else if (b[i] == 5)y = 20; 88 else y = G(b[i]); 89 for (int j = 1; j < c[i]; j++)y = y*b[i]; 90 s = s / gcd(s, y)*y; 91 } 92 } 93 return s; 94 } 95 int main(){ 96 memset(GG, -1, sizeof GG); 97 int stop = sqrt(1.0 * 1000000); 98 for (int i = 2; i <= stop; i++) 99 if (!prv[i]) 100 for (int j = i*i; j <= 1000000; j += i) 101 if (!prv[j])prv[j] = 1; 102 for (int i = 2; i <= 1000000; i++)if (!prv[i])pri[cnt++] = i; 103 int T; scanf("%d", &T); 104 while (T--){ 105 init(); 106 scanf("%d", &p); 107 ans = LOOP(p); 108 printf("%d\n", ans); 109 } 110 return 0; 111 }
2 5 5 13 5
0 3
据说是由
这两个公式推出下面的。。。
有了上面两个公式后，妈蛋才发现很明显嘛。。。智商低不解释！
1 #include <cstdio> 2 #include <cstring> 3 #include <queue> 4 #include <map> 5 #include <cmath> 6 #include <iostream> 7 #include <time.h> 8 #include <algorithm> 9 using namespace std; 10 #define FF(i,N) for(int i=0;i<2;i++) 11 #define ll long long 12 #define maxn (1<<15) 13 ll n, m, k, s, t, mod; 14 ll f[maxn]; 15 int main(){ 16 int T; cin >> T; 17 f[0] = 0; f[1] = 1; 18 for (int i = 2; i <= 1005; i++)f[i] = f[i - 1] + f[i - 2]; 19 while (T--){ 20 cin >> n >> m; 21 if ((n/m/2*m)%2 == 0)k = 1; 22 else k = -1; 23 if (n / m % 2 == 0)s = ((f[n%m] % f[m])*k+f[m])%f[m]; 24 else s = (((f[n%m] % f[m])*(f[m - 1] % f[m]) % f[m])*k + f[m]) % f[m]; 25 printf("%d\n", s); 26 } 27 return 0; 28 }
不会弄大数，这里给出小数据类似代码。。。用JAVA很方便，我也不会JAVA- -！
100
F(100)= 3 * 5^2 * 11 * 41 * 101 * 151 * 401 * 3001 * 570601
据说是论文题。。。
看了一下，吓尿。。。
是不是那个什么Lucas大数分解有关的。。。反正不明白。。。
http://mersennus.net/fibonacci/
http://mersennus.net/fibonacci/f1000.txt
6 ba
3
8001. Fibonacci Sum
Problem code: FIBOSUM
The fibonacci sequence is defined by the following relation:
F(0) = 0
F(1) = 1
F(N) = F(N - 1) + F(N - 2), N >= 2
Your task is very simple. Given two non-negative integers N and M, you have to calculate the sum (F(N) + F(N + 1) + ... + F(M)) mod 1000000007.
Input
The first line contains an integer T (the number of test cases). Then, T lines follow. Each test case consists of a single line with two non-negative integers N and M.
Output
For each test case you have to output a single line containing the answer for the task.
Example
Input: 3 0 3 3 5 10 19 Output: 4 10 10857
Constraints
- T <= 1000
- 0 <= N <= M <= 109
