康托展开和逆康托展开
妈妈再也不用担心生成全排列字典序很慢了!
首先用康托展开的公式镇楼:
X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a*0!
暂且不解释这个公式的意义,我们先看下面的问题。
有n=4个元素1,2,3,4,将四个元素组成的全排列按字典序排列。输入一个排列,输出次排列在字典序中的顺序数。
输入:
4123
输出:
19
如过采用暴力的方法解题,首先求出n个元素组成的全排列,然后字典序,查找位次。这样时间和空间复杂度都很高,于是康托展开应运而生。
康托展开是一个特殊的哈希函数,它将一个整数X展开成如下形式:
X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a*0!
其中,a为整数,并且0<=a[i]<i(1<=i<=n)
公式中,n表示在排列中的位数(注意这里从右侧开始,并且右侧第一位位数为0)
a[n]代表比在第n位的数字小并且没有在第n位之前出现过的数字的个数。
即a[n]代表着第n个数列在以第n个元素为开头的子数列中是“第几大”。
在本题中
当n=3时,4在以其为首的子排列“4123"中,4是第3大(注意这里是从0开始),则a[3]=3。
当n=2时,1在以其为首的子排列“123"中,1是第0大(注意这里是从0开始),则a[2]=0。
当n=3时,2在以其为首的子排列“23"中,D是第0大(注意这里是从0开始),则a[1]=0。
当n=3时,3在以其为首的子排列“3"中,D是第0大(注意这里是从0开始),则a[0]=0。
所以排列4123的顺序数为:X+1=3*3!+0*2!+0*1!+0*0!+1=19
注意这里的X也是从0开始,所以我们所求的顺序数为X+1。
所以这道题可以这么写:
1 #include<stdio.h> 2 #include<string.h> 3 4 int f(int x) 5 { 6 if(x==0)return 0; 7 int a=1; 8 while(x) 9 a*=x--; 10 return a; 11 } 12 13 int contor(char *s,int len) 14 { 15 int ans=0; 16 for(int i=0; i<len; i++) 17 { 18 int num=0; 19 for(int j=i+1; j<len; j++) 20 if(s[i]>s[j]) 21 num++; 22 ans+=num*f(len-i-1); 23 } 24 return ans; 25 } 26 27 int main() 28 { 29 char s[10]= {0}; 30 scanf("%s",&s); 31 printf("%d\n",contor(&s[0],strlen(s))+1); 32 return 0; 33 }
下面说一下我个人对康托展开的理解,对于A,B,C,D四个元素的全排列字典序,可以构造以下解答树:
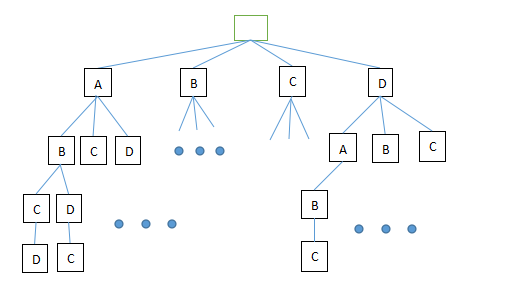
从根结点到最底层的一个子叶节点即为一个解,最底层从左到右排列解的顺序即为字典序。
对于一个排列,我们只需要知道在它之前有多少个排列即可知道它的位置,对于一个排列DABC,首先从第一个元素开始,直到最后一个元素,分别算出在他们对应节点层前面一共有多少个解,最后加和,即为在此排列前面的解数目。
对于每个元素,和它同层并在他前面的解数目为:和它同层并小于它的元素数目 * 和它同层每个元素下对应的解个数。
这时候我们就要翻出康托展开的公式了:
X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a*0!
其中,a为整数,并且0<=a[i]<i(1<=i<=n)
和它同层并小于它的元素数目其实就是公式中的a[n],和它同层每个元素下对应的解的个数即为(n-1)!。
依次求出每个元素的和该元素同层并在他前面的解数目并求和,即为康托展开的公式。
逆康托展开:
通过康托展开可以通过运算X的值得到一个排序的序数,同样,如果有一个X值,也能得到对应的序列,这样即可在较小时间空间复杂度的情况下,得到或遍历所有排序,也能得到特定序数的排列。
对于康托展开的公式而言:
X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a*1!+a*0!
其中,a为整数,并且0<=a[i]<i(1<=i<=n)
如果得知一个整数X,那么就可以通过辗转相除的方法得到该序列:
例如,以A,B,C,D四个元素组成的全排列的字典序中,第16个序列是什么?
首先用16-1得到15(因为康托展开中以0为开头)
然后开始辗转相除:
15%3!=2余3 第一位是ABCD四个元素中第2大的元素C(从0开始),C
3%2!=1余1 第二位是ABD三个元素中第1大的元素,B
1%1!=1余0 第三位是AD两个元素中第0大的元素,A
0%0!=0余0 第四位是D一个元素中第0大的元素,D
所以第16个排列为:CBAD


 浙公网安备 33010602011771号
浙公网安备 33010602011771号