树状数组
求区间和的问题
当前有一个包含n个元素的数组arr[n]，需要不断地修改其中某一元素的值，以及查询某一区间的和。
最为原始的做法就是直接修改值，然后遍历求和，那么修改的时间复杂度就是\(O(1)\)，查询的时间复杂度就是\(O(n)\)。
或者采用前缀和的形式，arr[i]记录的是0到i元素的和，这样查询区间和的复杂度就降为\(O(1)\)了，但是修改区间和的复杂度变为了\(O(n)\)。这样只适合查询很多，修改很少的场景。
树状数组
树状数组就是为了解决上面同时存在修改和查询的问题。树状数组用二进制的方式来划分区间，从而达到修改和查询的时间复杂度均为\(O(lgn)\)。
树状数组也是利用求前缀和的形式来算区间和，但是不是遍历求前缀和，而是将二进制划分的区间相加得到前缀和。
这里二进制的思想就是，对于任意一个数，其二进制表达都是0，1的序列，可以通过每一位上的1相加得到，比如
\[\begin{align}
6&=0110\notag \\
&=0100+0010\notag \\
\end{align}\]
要实现区间也能像二进制一样加起来，树状数组引入了lowbit函数，lowbit(i)取i中最低的为1的二进制位。然后规定arr[i]表示从第i个元素往前数lowbit(i)个元素得到一个区间。
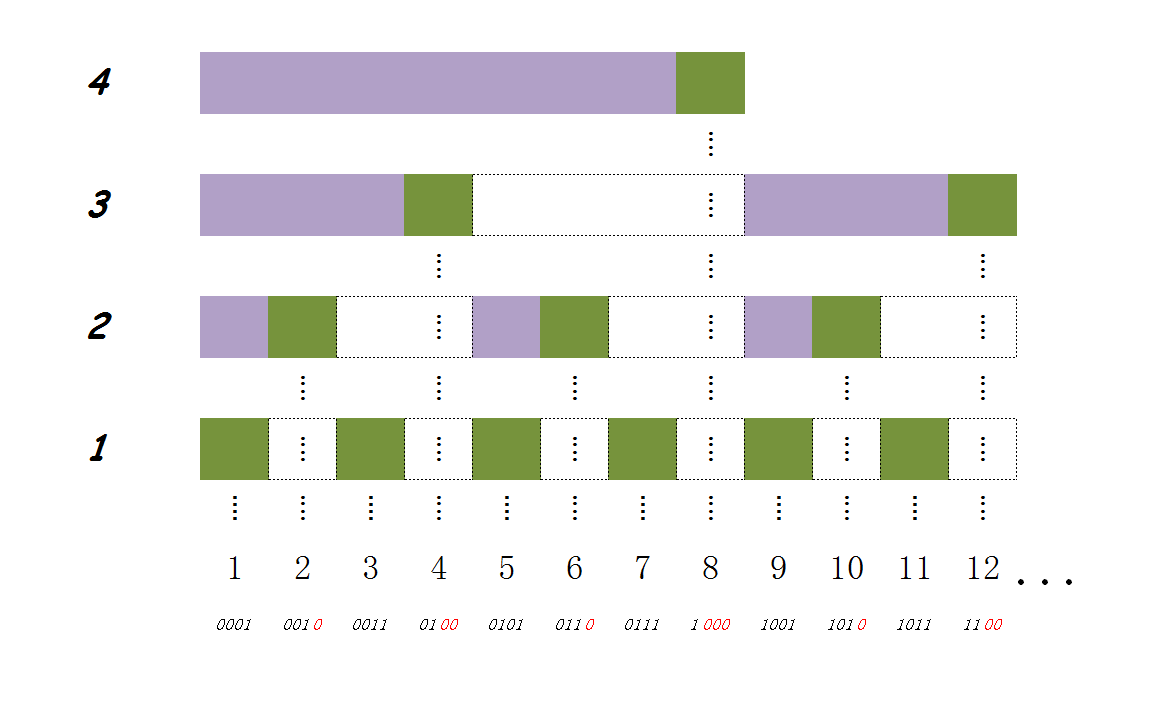
这样一来，要求任意的前缀和，只要不断地计算i = i - lowbit(i)，直到i == 0就行了。这里执行的次数，就是i的二进制表示中1的数量，所以复杂度为\(O(lgn)\)。
对于修改某一元素，例如对于元素arr[i]，其直接父层可以通过计算i = i + lowbit(i)计算得到，不断找影响到的父层，直到i > n就行了。所以复杂度也为\(O(lgn)\)。
代码示例（go）
package main
import "fmt"
func lowbit(x int) int {
return x & -x
}
// 将arr[idx]的值加上val
func add(arr []int, idx, val int) {
idx++
for idx <= len(arr) {
arr[idx-1] += val
idx += lowbit(idx)
}
}
// 求[0,idx]的前缀和
func prefixSum(arr []int, idx int) int {
var ans int
idx++
for idx != 0 {
ans += arr[idx-1]
idx -= lowbit(idx)
}
return ans
}
// 求[i,j]的区间和
func intervalSum(arr []int, i, j int) int {
return prefixSum(arr, j) - prefixSum(arr, i-1)
}
// 在原数组上初始化树状数组
func initBIT(arr []int) {
for i := len(arr) - 2; i >= 0; i-- {
val := arr[i]
arr[i] = 0
add(arr, i, val)
}
}
func main() {
arr := []int{4, 2, 7, 5, 9, 1, 0, 3}
initBIT(arr)
for i := 0; i < len(arr); i++ {
fmt.Println(prefixSum(arr, i))
}
for i := 0; i < len(arr); i++ {
for j := i + 1; j < len(arr); j++ {
fmt.Println(i, j, intervalSum(arr, i, j))
}
}
}
