堆（heap）

堆（heap）

（二叉）堆是一种用数组表示的完全二叉树，并且任意节点满足\(A[PARENT(i)]\geq A[i]\)的大小关系（最大堆）：

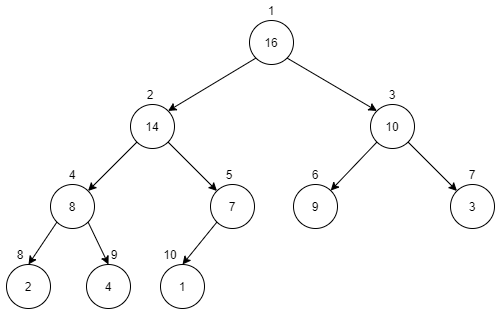
完全二叉树：对于高度为h的二叉树，除了h层以外，其余0到h-1层的节点都是满的，且h层的节点都靠左边。

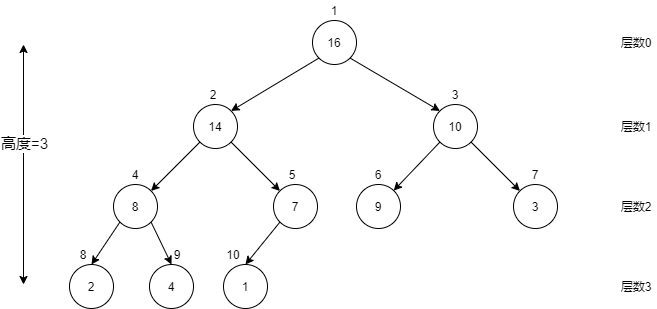
完全二叉树高度：对于n个节点的完全二叉树，高度为\(\lfloor \log n\rfloor\)：
证明：
对于拥有\(2^h \leq n \leq 2^{(h+1)}-1\)个节点的完全二叉树的高度都是h
所以根据\(h \leq \log n < (h+1)\)推出，n个节点的完全二叉树高度为\(\lfloor \log n\rfloor\)

建堆（makeHeap）

建堆的过程就是将初始化输入的数组重新排列，使其满足\(A[PARENT(i)]\geq A[i]\)的大小关系。
假设对于元素\(A[i]\)，其左右子节点\(A[LEFT(i)]\)和\(A[RIGHT(i)]\)作为根的二叉树已经满足堆的顺序性质了，那么这时只要将元素\(A[i]\)不断和左右子节点进行比较，并将\(A[i]\)和最大的子节点交换顺序，直到\(A[i]\)就是最大的节点，或者\(A[i]\)变为了叶子节点。最终就得到了更大的堆，不断进行这个过程，将子堆两两合并，最终整个数组就变成了一个完整的堆了。
这里有个很巧妙的计算过程，那就是从\(A[PARENT(heapSize)]\)节点递减遍历到节点\(A[1]\)，对每个节点执行上述的步骤，便完成了建堆操作：

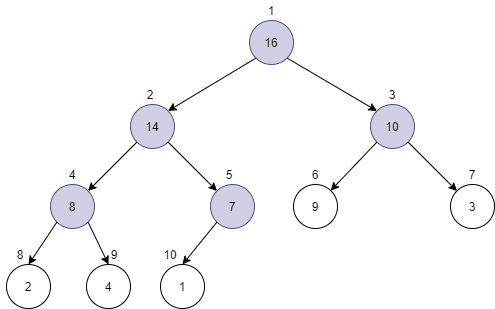
• 代码实现（C++）：

#include <utility>

#define PARENT(i) (i / 2)
#define LEFT(i) (i * 2)
#define RIGHT(i) (i * 2 + 1)

template<typename RandomAccessIterator, typename SizeType, typename Compare>
void heapify(RandomAccessIterator first, SizeType i, SizeType size, Compare comp) {
    auto val = std::move(*(first + i - 1));
    for (auto child = RIGHT(i); child <= size; i = child, child = RIGHT(i)) {
        if (comp(*(first + child -1 - 1), *(first + child - 1))) {
            --child;
        }
        if (comp(val, *(first + child - 1))) {
            *(first + i - 1) = std::move(val);
            return;
        }
        *(first + i - 1) = std::move(*(first + child - 1));
    }
    auto leftChild = LEFT(i);
    if (leftChild <= size && !comp(val, *(first + leftChild - 1))) {
        *(first + i - 1) = std::move(*(first + leftChild - 1));
        i = leftChild;
    }
    *(first + i - 1) = std::move(val);
}

template<typename RandomAccessIterator, typename Compare>
void makeHeap(RandomAccessIterator first, RandomAccessIterator last, Compare comp) {
    auto size = last - first;
    for (auto i = PARENT(size); i > 0; --i) {
        heapify(first, i, size, comp);
    }
}

#undef PARENT
#undef LEFT
#undef RIGHT

• 算法复杂度
  • 最好情况：当输入数组本身就满足堆的顺序性质，那么遍历的时候什么也不用做，总共遍历了\(\frac{n}{2}\)个元素，时间复杂度为\(\Theta(n)\)
  • 最坏情况：当输入的数组逆序，每个元素都需要下降到叶子节点，时间复杂度为\(\Theta(n)\)

最坏情况计算过程：
对于包含\(2^h \leq n \leq 2^{(h+1)}-1\)个元素的堆，\(h-2\)层最多包含\(2^{(h-2)}\)个元素，每个元素最多下降2次，\(h-3\)层最多包含\(2^{h-3}\)个元素，每个元素最多下降3次，以此类推得到总的下降次数：

\[\sum_{i=1}^{h-1}{(h-i+1)2^{i-1}} \]

由于等差乘等比数列公式\(\sum_{i=1}^{n}{(an+b)q^{n-1}}=(An+B)q^n-B\)，其中\(A=\frac{a}{q-1}\)，\(B=\frac{b-A}{q-1}\)，所以上式中\(A=\frac{-1}{2-1}=-1\)，\(B=\frac{h+1+1}{2-1}=h+2\)

\[\begin{align} \sum_{i=1}^{h-1}{(h-i+1)2^{i-1}} &= (-(h-1)+h+2)2^{h-1}-h-2\\ &= 3\cdot 2^{h-1}-h-2\\ \end{align}\]

对于第\(h-1\)层的元素单独计算，这里面有\(\frac{n}{2}-2^{h-1}+1\)个元素最多下降1次
最后还有一个地方没有考虑到，那就是对于下降到\((\frac{n}{2},2^h)\)这些节点的元素，由于这里已经是叶子节点了，所以之前的计算多计算了一次下降过程，且多计算的次数刚好就是这些节点数，所以最后得到:

\[\begin{align} 3\cdot 2^{h-1}-h-2 + \frac{n}{2}-2^{h-1}+1 - (2^h-\frac{n}{2}) &= n-h-1\\ &= n-\lfloor \log n\rfloor-1\\ \end{align}\]

这个结果不一定完全准确，但已经和最坏情况很接近很接近了，算法导论里面的方法估算出的是\(2n\)，比这里\(n-\lfloor \log n\rfloor-1\)的界要松。